Theorem 10.5 : There is one and only one circle passing through three given non-collinear points.

Video Solution

Text Solution

Verified by Experts

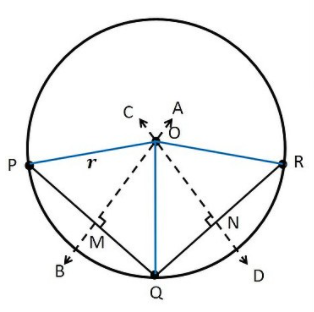
In $△ O P M$ and $△ O Q M$
$O M = O M$ (common)
$∠ O M P = ∠ O M Q$ (Perpendicular angles)
$P M = Q M$
By SAS congruency, $△ O P M$ and $△ O Q M$ are congruent.
$O P = O Q$
Similarly, we can prove that, $O Q = O R$
Thus,
$O P = O Q = O R$
Taking, $O$ as center and $O P$ as radius construct a circle. Hence circle passes through $P$ , $Q$ , $R$ .
Hence points are concyclic.

Updated on:21/07/2023