Chords equidistant from the center of a circle are equal in length.

Video Solution

Text Solution

Verified by Experts

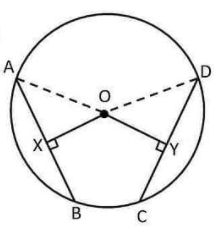
In $△ A O X$ and $△ D O Y$
$∠ O X A = ∠ O Y D$ (perpendicular angles)
$O A = O D$ (radius)
$O X = O Y$ (given)
By RHS congruency, $△ A O X$ and $△ D O Y$ are congreunt.
$A X = D Y$ (CPCT)
For chord $A B$
$O X ⊥ A B$
Perpendiculars from center to chord bisects the chord.
$A B = 2 A X$
Similarly, for chord $C D$
$C D = 2 D Y$
Thus,
$A X = D Y$
$2 A Y = 2 D Y$
$A B = C D$ .

|

Updated on:21/07/2023

Class 9 MATHS NCERT THEOREMS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
r : Two chords of a circle are equidistant from the centre if and only if they are equal in length
Statements r can be interpreted as
AIf two polygons are congruent then they are equal in shape and size
BIf two polygons are equal in shape and size then· they' are not congruent
CBoth (1) & (2)
DNoen of these
Question 2 - Select One
Calculate the angle subtended by the chord at the point on the major arc if the radius and the chord of the circle are equal in length
AA) $30^{\circ}$
BB) $120^{\circ}$
CC) $200^{\circ}$
DD) $300^{\circ}$
Question 3 - Select One
If a chord of length 16 cm is at a distance of 15 cm from the centre of the circle, then the length of the chord of the same circle which is at a distance of 8 cm from the centre is equal to
A10 cm
B20 cm
C30 cm
D40 cm

NCERT-NCERT THEOREMS-THEOREM 10.7

Chords equidistant from the center of a circle are equal in length.
08:03

Home
Ask Doubt
Profile