Theorem 10.6 : Equal chords of a circle (or of congruent circles) are equidistant from the centre (or centres).

Video Solution

Text Solution

Verified by Experts

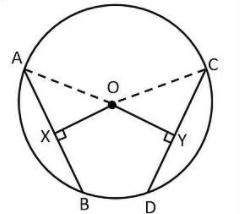
Since $O X ⊥ A B$
Perpendicular from the center to the chord, bisects the chord,
$A X = B X = \frac{A B}{2}$
Similarly,
$C Y = D Y = \frac{C D}{2}$
$A B = C D$ (given)
Thus,
$A X = C Y$
In $△ A O X$ and $△ C O Y$ ,
$∠ O X A = ∠ O Y C$ (Perpendicular angles)
$O A - O C$ (radius)
$A X = C Y$
By RHS rule, $△ A O X$ and $△ C O Y$ are congruent.
$O X = O Y$ (CPCT)

|

Updated on:21/07/2023

Class 9 MATHS NCERT THEOREMS

Topper's Solved these Questions

Similar Questions

NCERT-NCERT THEOREMS-THEOREM 10.6

Theorem 10.6 : Equal chords of a circle (or of congruent circles) are ...
04:51

Home
Ask Doubt
Profile