The points P(3,2,4),Q(4,5,2),R(5,8,0)andS(2,−1,6) are
A
vertices of a rhombus which is not a square
B
non-coplanar
C
collinear
D
copanar but not collinear
Video Solution
Text Solution
The correct Answer is:C
P(3,2,4),Q(4,5,2),R(5,8,0),S(2,−1,6)
PQ=√(4−3)2+(5−2)2+(2−4)2
=√1+9+4=√14
QR=√(5−4)2+(8−5)2+(0−2)2
=√1+9+4=√14
RS=√(2−5)2+(−1−8)2+(6−0)2
=√9+81+4=√14
PS=√(2−3)2+(−1−2)2+(6−4)2
=√1+9+4=√14
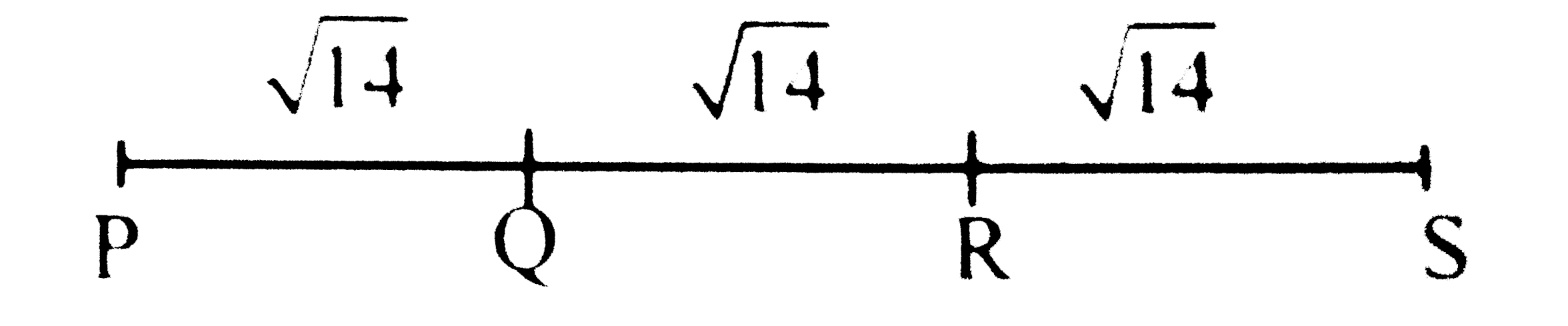
Since, PQ+QR−PS=RS, points are collinear.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
The point P (3,2,4),Q(4,52),R(5,8,0)andS(2,−1,6) are :
AVertices of a rhombus which is not a squareBNon coplanarCCollinearDCoplanar but not collinearPoints (3, 2, 4), (4,5,2), (5,8, 0) are
AcollinearBvertices of equilateral triangleCvertices of isosceles triangleDNone of theseIf the points A(4,5,2),B(3,2,p)andC(5,8,0) are collinear , then p=
A−4B4C0D2
Show that the points P(−3,−2,4),Q(−9,−8,10)andR(−5,−4,6) are collineasr and R divides PQ in the ratio 1:2
View SolutionJuatify that the four points P(−2,−7),Q(2,−4),R(−1,0) and S(−5,−3) are the vertices of a square.
View SolutionShow that the points P(0,2) Q(3,-1) R(-2,-6) and S(-5,-3) are the verties of a rectangle.
View SolutionUsing direction numbers show that the points P(4,7,8)andQ(2,3,4),R(−1,−2,1)andS(1,2,5) taken in ordethe vertices of a parallelogram. Is the parallelogram rectangle?
View SolutionThe value of λ for which the points L(1,0,3),M(−1,3,4),N(1,2,1)andP(λ,2,5) are coplanar is
View Solution
