Let Z1andZ2, be two distinct complex numbers and let w=(1−t)z1+tz2for some number "t" with o
A
|z−z2|+|z−z2|=|z1−z2|
B
arg(z−z1)=arg(z−z2)
C
∣∣∣z−z1¯z−¯z1z2−z1¯z2−¯z1∣∣∣=0
D
arg(z−z1)=arg(z2−z1)
Video Solution
Text Solution
The correct Answer is:B
Let z1 and z2 be represented by points A and B respectively in the Argand plane.
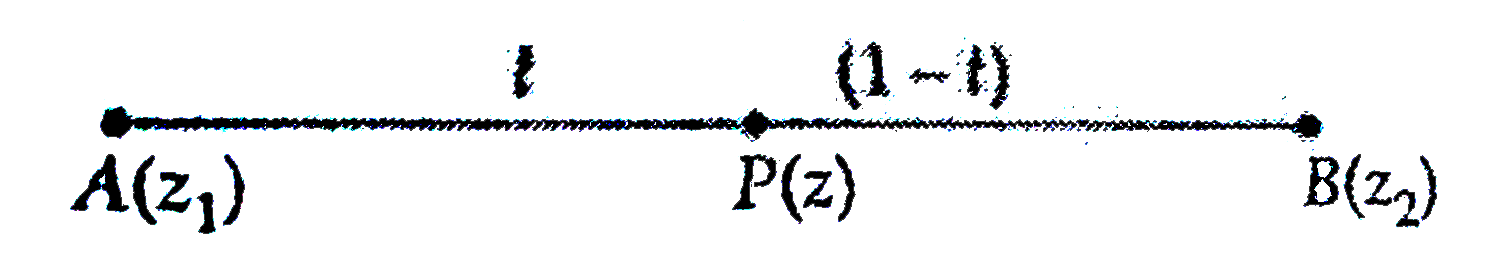
We have,
z=(1−t)z1+tz2(1−t)+t
⇒ z represents a point P dividing AB in the ratio t:(1−t)
Clearly, AP+PB=AB
⇒|z−z1|+|z−z2|=|z1−z2|
So, option (a) is true.
Since, A,P,B are collinear. Therefore,
arg(¯¯¯AP)=arg(¯¯¯AB)⇒arg(z−z1)=arg(z2−z1)
So, option (d) is correct.
We have,
z=(1−t)z1+tz2
⇒t=z−z1z2−z1 is purely real
⇒|(z−z1,¯z−¯z1),(z2−z1,¯z2,¯z1)|=0
Hence, option (c) is correct.
We have,
arg(z−z1)=arg(¯¯¯AP) and arg(z−z−(2))=arg(¯¯¯BP)
Clearly, arg(¯¯¯AP)−arg(z−z2)≠0
So, option (b) is not correct.
|
Topper's Solved these Questions
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Section II - Assertion Reason Type
15 Videos
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Exercise
131 Videos
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test
59 Videos
- CIRCLESBOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Chapter Test
55 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - OBJECTIVE RD SHARMACHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise
86 Videos
Similar Questions
Knowledge Check
Let z1 and z2 be two distinct complex numbers and z=(1−t)z1+iz2, for some real number t with 0<t<1 and i=√−1. If arg(w) denotes the principal argument of a non-zero compolex number w, then
A|z−z1|+|z−z2 =|z1−z2∣Barg(z−z1)=arg(z−z2)C∣∣∣z−z1¯z−¯z1z2−z1¯z2−¯z1∣∣∣=0Darg(z−z1)=arg(z2−z1)Let z1 and z2 be two distinct complex numbers and z=(1−t)z1+iz2, for some real number t with 0<t<1 and i=√−1. If arg(w) denotes the principal argument of a non-zero compolex number w, then
A|z−z1|+|z−z2|=|z1−z2|Barg(z−z1)=arg(z−z2)C∣∣∣z−z1¯z−¯z1z2−z1¯z2−¯z1∣∣∣=0Darg(z−z1)=arg(z2−z1)Let Z1 and Z2 are two non-zero complex number such that |Z1+Z2|=|Z1|=|Z2|, then Z1Z2 may be :
A1+ωB1+ω2CωDω2
If z1andz2 are two complex numbers such that z1+2,1−z2,1−z, then
View SolutionLet z1,z2,z3 be three distinct complex numbers satisfying |z1−1|=|z2−1|=|z3−1|. Let A , B, and C be the points represented in the Argand plane corresponding to z1,z2andz3 respectively. Prove that z1+z2+z3=3 if and only if ΔABC is an equilateral triangle.
View SolutionLet Z and w be two complex number such that |zw|=1 and arg(z)−arg(w)=π/2 then
View SolutionIf z1andz2 are two distinct non-zero complex number such that |z1|=|z2|, then z1+z2z1−z2 is always
View SolutionIf z1 and z2 are two complex numbers such that z1z2+z2z1=1, then
View Solution
