The minimum value of |z1−z2| as z1 and z2 vary over the curves ∣∣√3(1−2z)+2i∣∣=2√7 and ∣∣√3(−1−z)−2i∣∣=∣∣√3(9−z)+18i∣∣ respectively is
A
7√72√3
B
5√72√3
C
14√7√3
D
7√75√3
Text Solution
The correct Answer is:B
We have,
∣∣√3(1−2z)+2i∣∣=2√7
∣∣√3(1−2z)+2i∣∣=2√7
⇒∣∣−2√3z+(√3+2i)∣∣=2√7
⇒∣∣
∣∣z−(12+1√3i)∣∣
∣∣=√73
Clearly, it represents a circle haivng center at (1/2,1/√3) and radius r1=√73. it is given that z1 lies on (i)
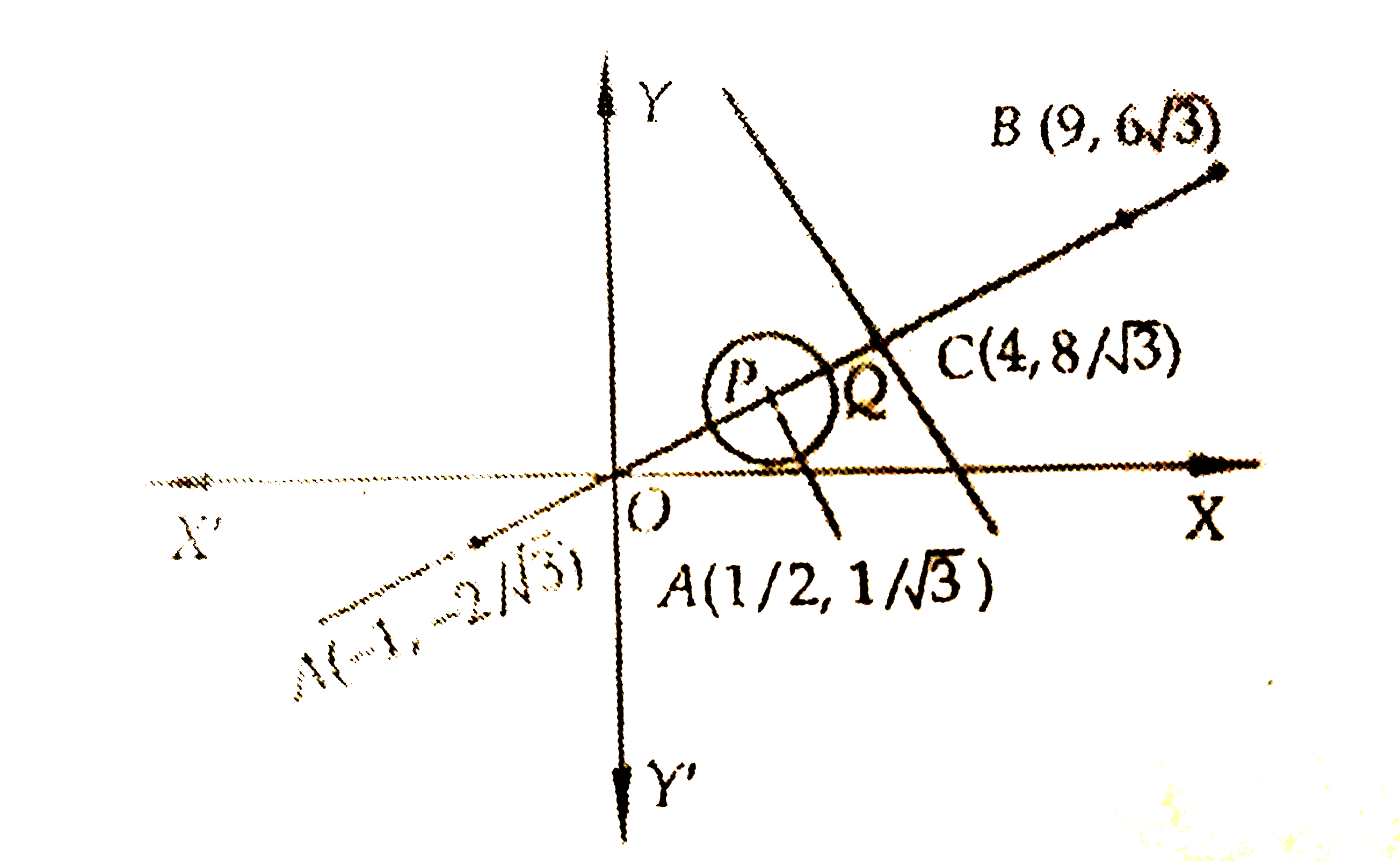
The equation of another curve is
∣∣√3(−1−z)−2i∣∣=∣∣√3(9−z)+18i∣∣
or ∣∣∣−1−z−2√3i∣∣∣=∣∣9−z+6√3i∣∣
or ,∣∣∣z+1+2√3i∣∣∣=∣∣z−9−6√3i∣∣
or ,∣∣
∣∣z−(−1−2√3i)∣∣
∣∣=∣∣z−(9+6√3i)∣∣
This, represents perpendicular bisector of the line segement joining point A(−1,−2√3) and B(9,6√3). The coordinates of the mid-point C of AB are (4,8/√3). Clearly, A,B and the center of the circle are collinear.
|
Topper's Solved these Questions
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Section II - Assertion Reason Type
15 Videos
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Exercise
131 Videos
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test
59 Videos
- CIRCLESBOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Chapter Test
55 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - OBJECTIVE RD SHARMACHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise
86 Videos
Similar Questions
Knowledge Check
z1andz2 are two complex numbers with different moduli, then ∣∣√3z1+i√2z2∣∣2+∣∣√2z1+i√3z2∣∣2 is equal to
A0B2|z1|2+3|z2|2C<5(|z1|2+|z2|2)D>10|z1z2|If |z1|=2and(1−i)z2+(1+i)¯z2=8√2, then
Aminimum value of |z1−z2| is 1Bminimum value of |z1−z2| is 2Cmaximum value of |z1−z2| is 8Dmaximum value of |z1−z2| is 4The value of (1+Iz+z5+z8)9 when z=√3+i2 is
A0B−1C−iD(−1+i)9
If z1=iz2andz1−z3=i(z3−z2),then prove that |z3|=√2|z1|.
View SolutionLet z1=(1+√3i)2(√3−i)1−iandz2=(√3+i)2(1−√3i)1+i then
View SolutionIf |z1|=|z2|=|z3|=1 are twu complex numbers such that |z1|=|z2|=√2 and |z1+z2|=√3 , then |z1−z2| equation
View SolutionFind the argument s of z1=5+5i,z2=−4+4i,z3=−3−3iandz42−2i,
wherei=√−1.
View SolutionIf z1=iz2andz1−z3=i(z3−z2),then prove that |z3|=√2|z1|.
View Solution
