Let w = (√3+ι2) and P={wn:n=1,2,3,.....}, Further H1={z∈C:Re(z)>12}andH2={z∈c:Re(z)<−12} Where C is set of all complex numbers. If z1∈P∩H1,z2∈P∩H2 and O represent the origin, then ∠Z1OZ2 =

A

π2,5π6

B

π,2π3

C

2π3,5π3

D

5π3,7π3

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:B

We have, ω=√32+12i=cosπ6+isinπ6
⇒ωn=cos(nπ)6+isin(nπ)6,n=1,2,3,…………
∴P={ωn,n=1,2,3,…..}={cos(nπ)6+isin(nπ)6,n=1,2,3,….}
ocr_image
Now, z1∈P⌢H1
⇒z1∈P and z1∈H1
⇒z1cos(nπ)6+isin(nπ)6 for some n∈Z and Re (z1)>12
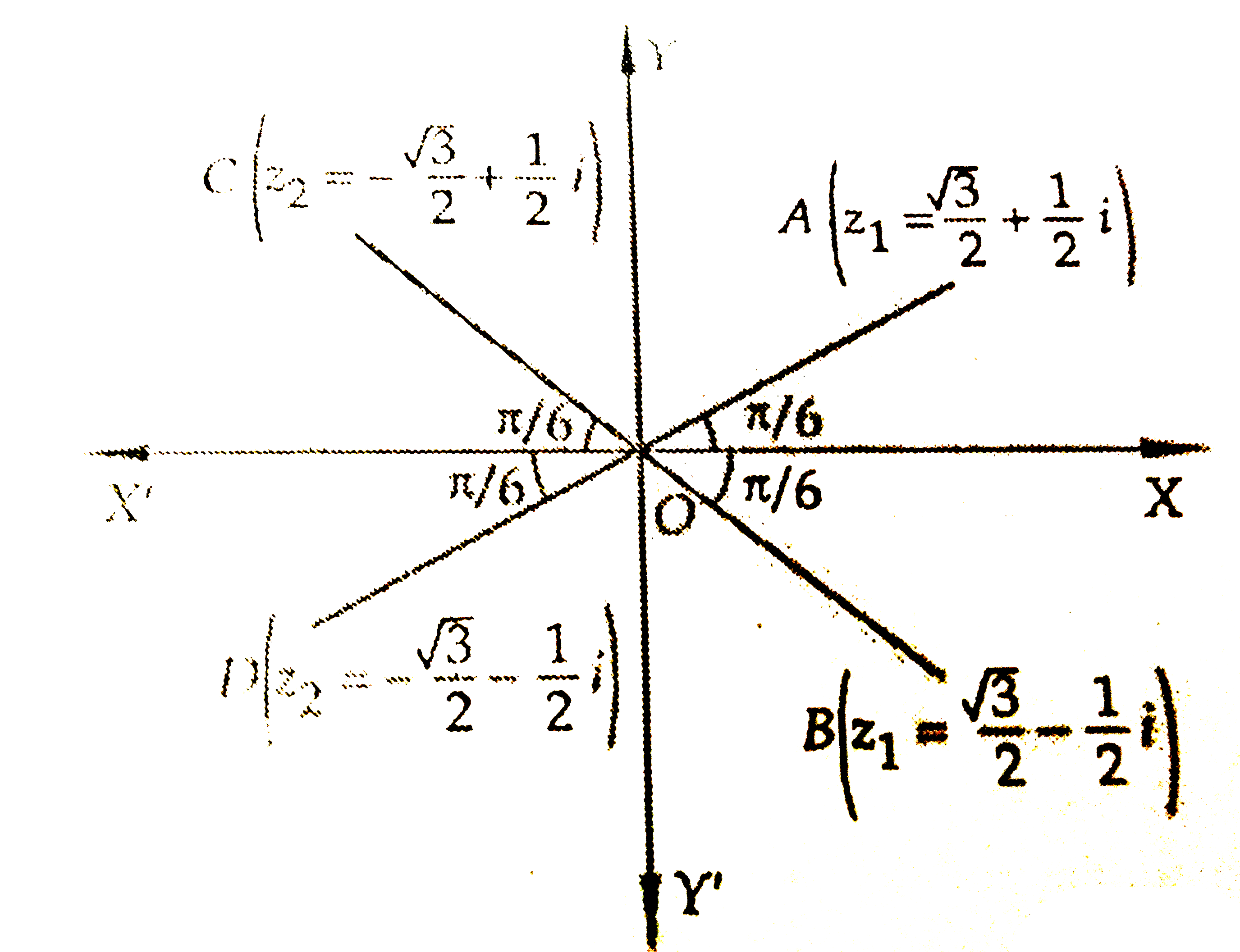
⇒z1=√22+12i,√32−12i
z2∈P⌢H2
⇒z2∈P and z2∈H2
⇒z2=cos(nπ)6+isin(nπ)6 for some n∈N and Re z2<−12
⇒z2=−√32+12i,−√32−12i
If z1=√32+12i and z2=−√32+12i, then
∠z1Oz2=∠AOC=π−(π6+π6)=2π3
If z1=√32+12i and z2=−√32−12i, then
∠z1Oz2=∠AOD=π
If z1=√32+12i and z2=−√32−12i, then
If z1=√32−12i and z2=−√32−12i, then
∠z1Oz2=∠BOD=2π3
Ifz1=√32−12i and z2=−√32+12i, then
∠z1Oz2=∠BOC=π
Hence, ∠z1Oz2=π or 2π3

Updated on:21/07/2023
|
Class 12MATHSCOMPLEX NUMBERS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Let ω=√3+i2 and P={Wn:n1,2,3………} further
    H1={z∈C:Re(z)>12}
    and H2={z∈C:Re(z)<−12}, where C is the set of all complex numbers. If z∈P∩H2 and 0 represents the origin then ∠z10z2=

    Aπ2
    Bπ6
    C2π3
    D5π6

  • If z1,z2,z3 are in H.P., they lie on a

    Acircle
    Bsphere
    Cstraight line
    Dnone of these

  • Let C be the set of all complex numbers. Let Si={z in C||z-3-2i|^(2)=8}, S2= {z∈C∣|z−¯z|≥8} and S3= {z∈C∣Re(z)≥5}. Then the number of elements in S1∩S2∩S3 is equal to

    A1
    B0
    C2
    DInfinite