If decompositon reaction A(g)toB(g) follows first order linetics then the graph of rate of formation (R ) of B against time t will be :Solution in Punjabi

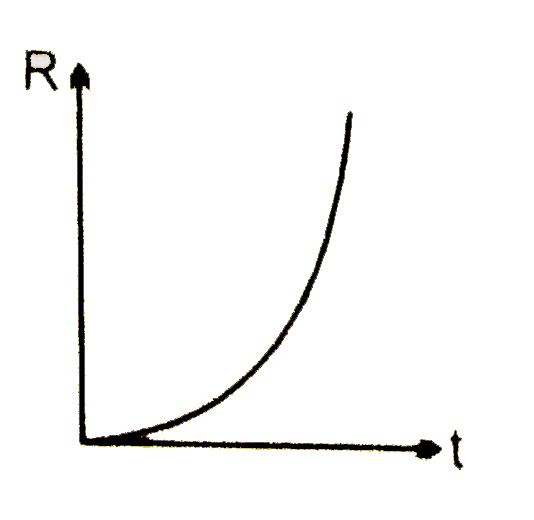
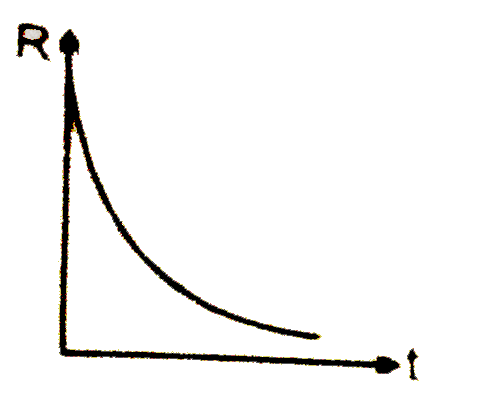
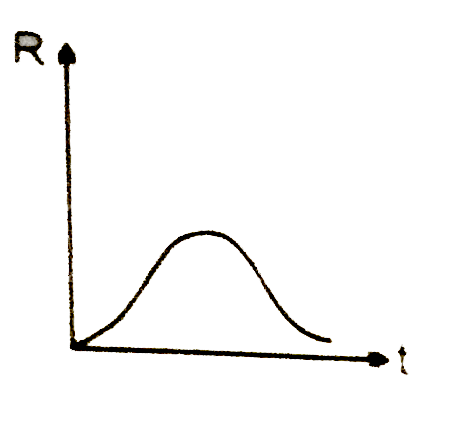
The correct Answer is:C
Step by step video & image solution for If decompositon reaction A(g)toB(g) follows first order linetics then the graph of rate of formation (R ) of B against time t will be : by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - NARENDRA AWASTHICHAPTER - CHEMICAL KINETIC & NUCLEAR CHEMISTRYEXERCISE - Level 1 (Q.3 To Q.32)1videos
CHEMICAL KINETIC & NUCLEAR CHEMISTRY
- BOOK - NARENDRA AWASTHICHAPTER - CHEMICAL KINETIC & NUCLEAR CHEMISTRYEXERCISE - Level 1 (Q.33 To Q.62)2videos
CHEMICAL KINETIC & NUCLEAR CHEMISTRY
- BOOK - NARENDRA AWASTHICHAPTER - SURFACE CHEMISTRYEXERCISE - Level -21videos
SURFACE CHEMISTRY
Similar Questions
The following data pertain to reaction between A and B
S.No[A][B]RatemolL−1molL−1molL−1sec−1I1×10−22×10−22×10−4II2×10−22×10−24×10−4III2×10−24×10−28×10−4
Which of the following interference(s) can be drawn from the above data
(a) Rate constatnt of the reaction 10−4
(b) Rate law of reaction is k[A][B]
(c ) Rate of reaction increases four times on doubling the concentration of both the reactant Select the correct answer codes:
a) a,b and C
b) a and b
c) b and c
d) c alone01:38View Solutioncolumn Icolumn IIP.Zero order reaction1.t1/2α1[A]0Q.First order reaction2.t100%=[A]0/kR.second order reactions3.Involves at least two reactantsS.Pseudo unimolecular reaction4.[A]=[A]0e−kt
03:15View Solutionfor the graph below, select correct order of temperture ?
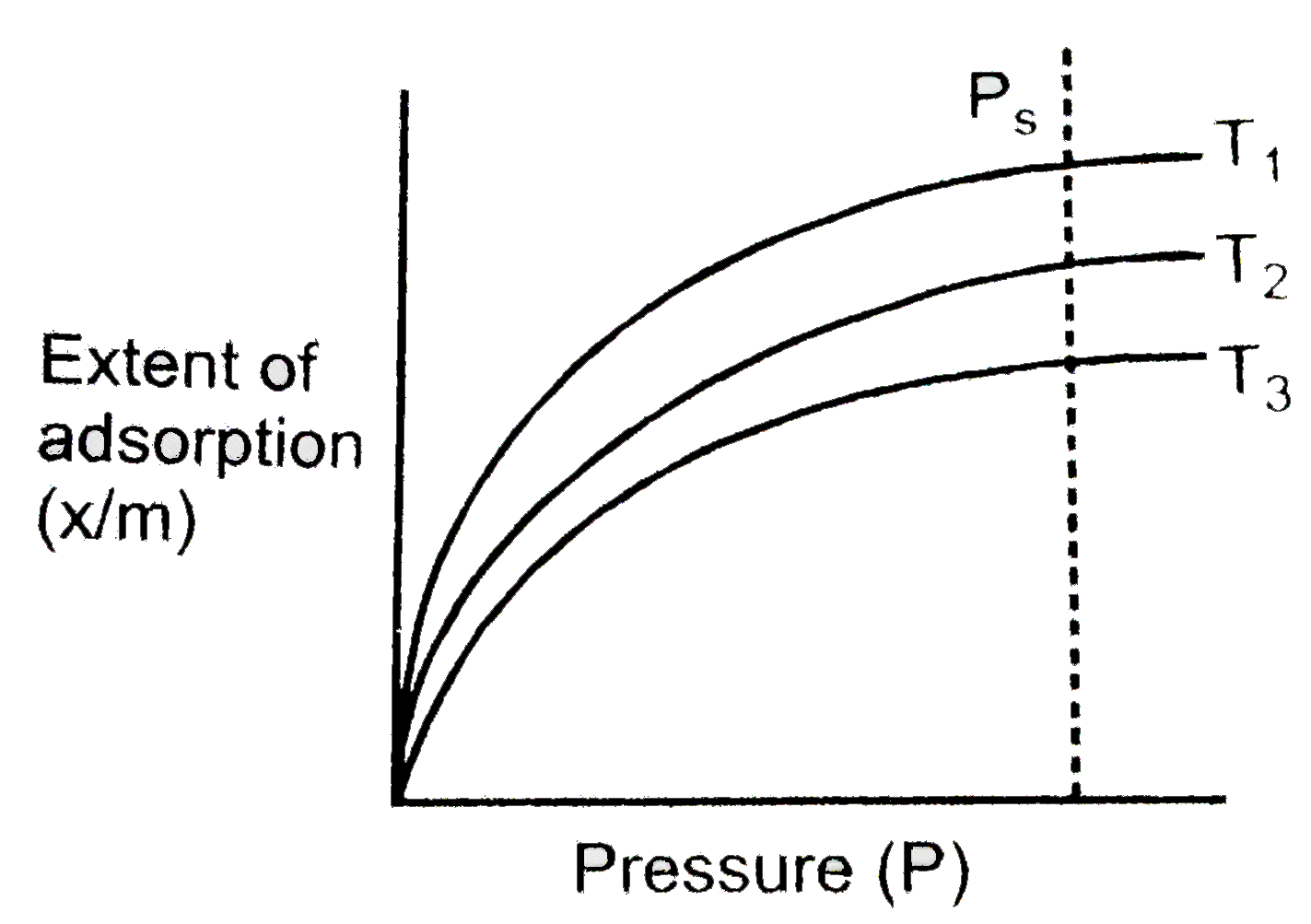 01:36View Solution
01:36View SolutionA radioactiev nuleus X deays to a stable nuleus Y . Then, time graph of rate of formation of Y against time t will be:
View SolutionWhich graph represents zero-order reaction [A(g)→B(g)] ?
03:42View SolutionIf decompositon reaction A(g)toB(g) follows first order linetics then the graph of rate of formation (R ) of B against time t will be :
03:52View SolutionIn the reaction
PCl5(g)⇔PCi3(g)+Ci2(g)
a graph in plotted to show the variation of rate of forward and backward reactions against time. Which of the following is correc?
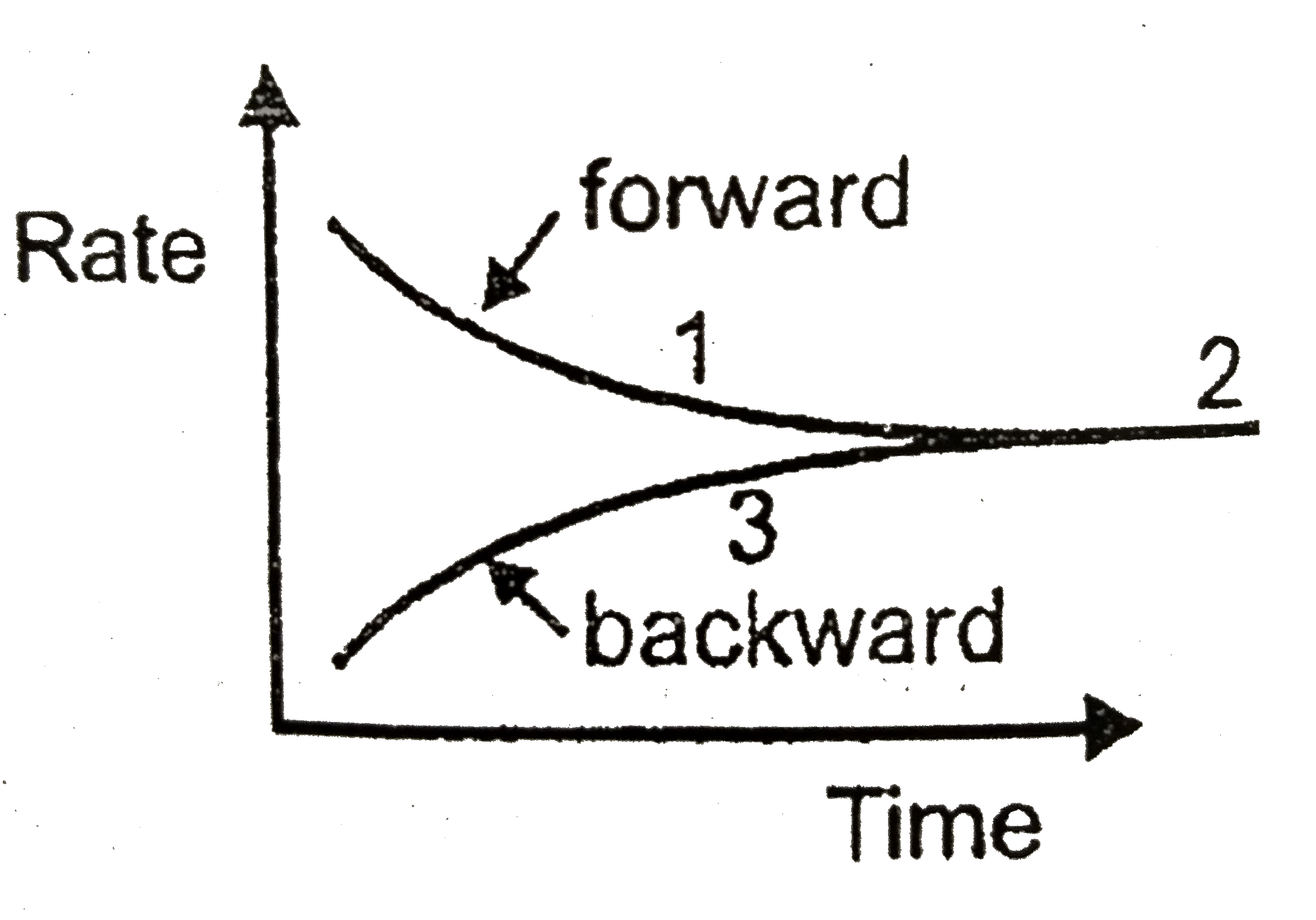
Q>KQ=KQ<KView SolutionFor a first order gas phase reaction :
A(g)→2B(g)+C(g)
P0 be initial pressure of A and Pt the total pressure at time 't'. Integrated rate equation is :03:27View SolutionGive two examples for each of zero order and first order reactions. Write the equations for the rate of reaction in terms of concentration changes of reactants and products for the following ractions. 1) A(g) +B(g) to C(g) +D(g) 2) A(g) to B(g)+C(g) 3) A(g) +B(g)to C(g)
View SolutionFor the first order gas phase decomposition reaction,
A(g)→B(g)+C(g)
if P0 is the initial pressure of A and Pt is total pressure after time t, then03:35View SolutionConsider a first order gas phase decomposition reaction given below : A(g)toB(g)+C(g) The initial pressure of the system before decomposition of A was P_(i) . After lapse of time 't', total pressure of the system increased by x units and became 'P_(t)' . The rate constant k for the reaction is given as ..................... .
05:31View SolutionFor the reaction : A(g) rarr B(g) + C(g) Concentration of 'A' varies with time (in sec) as : [A]_(T)=[10=0.2T^(2)]M The time at which rate of formation of 'B' is 1 M/sec.
04:20View SolutionFor a first order gas phase reaction : " "A(g)rarr2B(g)+C(g) P_(0) be initial pressure of A and P_(t) the total pressure at time 't' . Integrated rate equation is -
01:45View Solution2A(g)rarr2B(g)+3C(g) is a first order reaction . When the reaction started , the pressure of the system was P_(0) , and it was found to be P_(t) after time t . The rate constant of the reaction can be expressed by the equation -
View SolutionFor the reaction : 3A_((g))rarr 2B_((g)) , the rate of formation of 'B' at 298 K is represented as ln((d[B])/(dt))=-4.606+2ln[A] . The order of reaction is
01:36View SolutionIf decompositon reaction A(g)toB(g) follows first order linetics then the graph of rate of formation (R ) of B against time t will be :
02:49View Solution

