A 0.25 kg puck is initially stationary on an ice surface with negligible friction. At time t = 0, a horizontal force begins to move the puck. The force is given by →F=(12.0−3.00t2)ˆi, with →F in newtons and t in seconds, and it acts until its magnitude is zero. (a) What is the magnitude of the impulse on the puck from the force between t= 0.750 s and t = 1.25 s? (b) What is the change in momentum of the puck between t=0 and the instant at which F=0?
The correct Answer is:(a)4.47 N.s ; (b)(16 N.s) ˆi ;
To solve the given problem, we will break it down into two parts: (a) calculating the magnitude of the impulse on the puck from the force between t = 0.750 s and t = 1.250 s, and (b) determining the change in momentum of the puck between t = 0 and the instant at which the force becomes zero.
Part (a): Magnitude of Impulse
1. Identify the Force Function:
The force acting on the puck is given by:
→F=(12.0−3.00t2)^i (in newtons)
2. Impulse Calculation:
Impulse (J) is defined as the integral of force over time:
J=∫t2t1→Fdt
Here, t1=0.750 s and t2=1.250 s.
3. Set Up the Integral:
Substitute the force function into the integral:
J=∫1.2500.750(12.0−3.00t2)dt
4. Calculate the Integral:
- First, integrate 12.0:
∫12.0dt=12.0t
- Then, integrate −3.00t2:
∫−3.00t2dt=−t3
- Thus, the integral becomes:
J=(12.0t−t3)1.2500.750
5. Evaluate the Integral:
- Calculate at t=1.250:
12.0(1.250)−(1.250)3=15.0−1.953125=13.046875
- Calculate at t=0.750:
12.0(0.750)−(0.750)3=9.0−0.421875=8.578125
- Now, subtract:
J=13.046875−8.578125=4.46875 Ns
6. Final Result for Part (a):
The magnitude of the impulse is approximately:
J≈4.47 Ns
Part (b): Change in Momentum
1. Determine When the Force Becomes Zero:
Set the force function to zero:
12.0−3.00t2=0⟹3.00t2=12.0⟹t2=4⟹t=2.0 s
2. Calculate the Change in Momentum:
The change in momentum (Δp) is equal to the impulse over the entire time from t=0 to t=2.0:
Δp=∫2.00→Fdt=∫2.00(12.0−3.00t2)dt
3. Set Up the Integral:
Δp=(12.0t−t3)2.00
4. Evaluate the Integral:
- Calculate at t=2.0:
12.0(2.0)−(2.0)3=24.0−8.0=16.0
- Calculate at t=0:
12.0(0)−(0)3=0
- Now, subtract:
Δp=16.0−0=16.0 Ns
5. Final Result for Part (b):
The change in momentum of the puck is:
Δp=16.0 Ns
Summary of Results
- (a) The magnitude of the impulse on the puck between t=0.750 s and t=1.250 s is approximately 4.47 Ns.
- (b) The change in momentum of the puck between t=0 and the instant at which F=0 is 16.0 Ns.
The force acting on the puck is given by:
→F=(12.0−3.00t2)^i (in newtons)
Impulse (J) is defined as the integral of force over time:
J=∫t2t1→Fdt
Here, t1=0.750 s and t2=1.250 s.
Substitute the force function into the integral:
J=∫1.2500.750(12.0−3.00t2)dt
- First, integrate 12.0:
∫12.0dt=12.0t
- Then, integrate −3.00t2:
∫−3.00t2dt=−t3
- Thus, the integral becomes:
J=(12.0t−t3)1.2500.750
- Calculate at t=1.250:
12.0(1.250)−(1.250)3=15.0−1.953125=13.046875
- Calculate at t=0.750:
12.0(0.750)−(0.750)3=9.0−0.421875=8.578125
- Now, subtract:
J=13.046875−8.578125=4.46875 Ns
The magnitude of the impulse is approximately:
J≈4.47 Ns
Set the force function to zero:
12.0−3.00t2=0⟹3.00t2=12.0⟹t2=4⟹t=2.0 s
The change in momentum (Δp) is equal to the impulse over the entire time from t=0 to t=2.0:
Δp=∫2.00→Fdt=∫2.00(12.0−3.00t2)dt
Δp=(12.0t−t3)2.00
- Calculate at t=2.0:
12.0(2.0)−(2.0)3=24.0−8.0=16.0
- Calculate at t=0:
12.0(0)−(0)3=0
- Now, subtract:
Δp=16.0−0=16.0 Ns
The change in momentum of the puck is:
Δp=16.0 Ns
- (a) The magnitude of the impulse on the puck between t=0.750 s and t=1.250 s is approximately 4.47 Ns.
- (b) The change in momentum of the puck between t=0 and the instant at which F=0 is 16.0 Ns.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (Single Correct Choice )47videos
CENTER OF MASS
- BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (More than One Correct Choice)5videos
CENTER OF MASS
- BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (Integer )4videos
CENTER OF MASS
- BOOK - RESNICK AND HALLIDAYCHAPTER - CAPACITANCEEXERCISE - PRACTICE QUESTION (INTEGER TYPE)3videos
CAPACITANCE
- BOOK - RESNICK AND HALLIDAYCHAPTER - CIRCUITSEXERCISE - Practice Questions (Integer Type)3videos
CIRCUITS
Similar Questions
A ball is dropped from a height h on a floor. The coefficient of restitution for the collision between the ball and the floor is e. The total distance covered by the ball before it comes to the rest.
02:49View SolutionA point mass of 1 kg collides elastically with a stationary point mass of 5 kg. After their collision, the 1 kg mass reverses its direction and moves with a speed of 2 m/s. Which of the following statements are correct for the system of these two masses?
02:15View SolutionThere object A,B and C are kept is a straing line a fritionlas horizental surface . These have masses have increase on 2m and m repectively . The object A move toward B with a speed 9 m//s and makes as electic collision with a there after B makes complately inclesis with C . All motion over on the same strangth line . Find the first speed of the object C
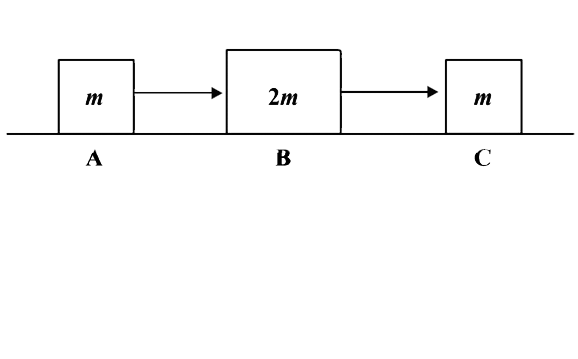 02:59View Solution
02:59View SolutionP and Q are two capacitors with capacitance 10μF and 20μF respectively which are connected in series with a battery of value 12V. Find the ratio between the charges and P and Q.
02:24View SolutionWhen two identical batteries of internal resistance 1Ω each are connected in series across a resistor R, the rate of heat produced in R is J1. When the same batteries are connected in parallel across R, the rate is J_2 = 2.25 J_2thenthevalueofR∈Omega is
06:51View SolutionAt t = 0 aparticle of mass m start moving from rest due to a force vecF = F_(0) sin (omega t)hati :
02:50View SolutionA small puck is sliding to the right with momentum →P1 on a horizontal, frictionless surface, as shown in figure. A force is applied to the puck for a short time and its momentum afterward is →Pf. Which lettered arrow shows the direction of the impulse that was delovered to the puck ?
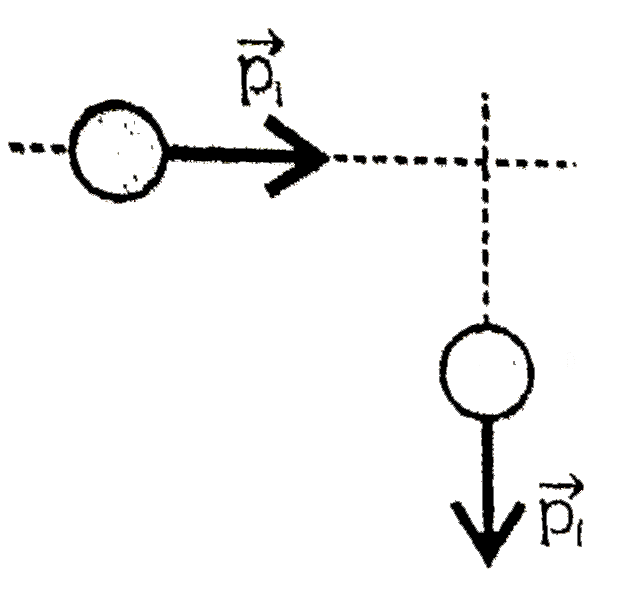 03:07View Solution
03:07View SolutionTwo pucks are initially moving along a frictionless surface as shown in the diagram. The pucks have mass m1<m2 and begin with equal magnitude of momentum. A constant force →F is applied to each puck direactly to the right for the same amount of non−zero time. After the pushes are complete, what is the relationship for the size of the moments of pucks (p1 and p2) ?
 01:42View Solution
01:42View SolutionA force →F=6t2ˆi+4tˆj is acting on a particle of mass 3 kg then what will be velocity of particle at t=3 second and if at t=0, particle is at rest:-
04:20View SolutionA body of mass 1 kg is acted upon by a force vecF=2sin3pithati+3cos3pithatj find its position t=1 sec if at t=0 it is at rest at origin.
02:14View SolutionThe magnitude of force (in Newtons) acting on a body varies with time (in micro second) as shown in the figure. The magnitude of total impulse of the force on the body from t = 4μs to t = 16μs is –
04:25View Solution3 किग्रा का एक पिंड विरामावस्था में है । यदि इस पर एक बल →F=6t2ˆi+4tˆj न्यूटन आरोपित किया जाये , तो t=3 सेकंड पर पिंड का वेग होगा -
04:06View SolutionDuring hockey practice, two pucks are sliding across the ice in the same direction. At one instant, a 0.18-kg puck is moving at 16 m/s while the other puck has a mass of 0.14 kg and a speed of 3.8 m/s. What is the velocity of the center of mass of the two pucks?
04:56View Solutionएक बल →F=6t2ˆi+4tˆj, 3 किग्रा द्रव्यमान के कण पर कार्यरत है, तो t = 3 सेकण्ड पर कण का वेग क्या होगा यदि t = 0 पर कण स्थिरावस्था में है?
03:50View SolutionThe magnitude of the force (in newtons) acting on a body varies with time t (in micro seconds) as shown in the fig AB, BC and CD are straight line segments. The magnitude of the total impulse of the force on the body from t=4μs to t=16μs is ….Ns
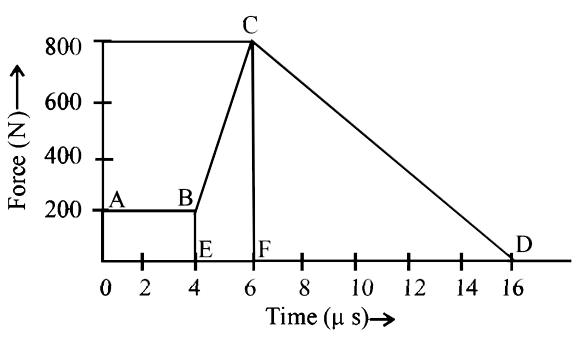 01:36View Solution
01:36View Solution

