A 0.70 kg ball moving horizontally at 6.0 m/s strikes a vertical wall and rebounds with speed 3.5 m/s. What is the magnitude of the change in its linear momentum?
The correct Answer is:6.7 kg. m/s
To find the magnitude of the change in linear momentum of the ball, we will follow these steps:
Step 1: Calculate the Initial Momentum
The initial momentum (Pi) of the ball can be calculated using the formula:
Pi=m⋅vi
where:
- m=0.70kg (mass of the ball)
- vi=6.0m/s (initial velocity)
Substituting the values:
Pi=0.70kg⋅6.0m/s=4.2kg m/s
Step 2: Calculate the Final Momentum
The final momentum (Pf) after the ball rebounds can be calculated similarly:
Pf=m⋅vf
where:
- vf=−3.5m/s (final velocity; negative because it is in the opposite direction)
Substituting the values:
Pf=0.70kg⋅(−3.5m/s)=−2.45kg m/s
Step 3: Calculate the Change in Momentum
The change in momentum (ΔP) is given by:
ΔP=Pf−Pi
Substituting the values:
ΔP=−2.45kg m/s−4.2kg m/s=−6.65kg m/s
Step 4: Calculate the Magnitude of the Change in Momentum
The magnitude of the change in momentum is the absolute value of ΔP:
|ΔP|=|−6.65kg m/s|=6.65kg m/s
Final Answer
The magnitude of the change in linear momentum is:
6.65kg m/s
---
The initial momentum (Pi) of the ball can be calculated using the formula:
Pi=m⋅vi
where:
- m=0.70kg (mass of the ball)
- vi=6.0m/s (initial velocity)
Pi=0.70kg⋅6.0m/s=4.2kg m/s
The final momentum (Pf) after the ball rebounds can be calculated similarly:
Pf=m⋅vf
where:
- vf=−3.5m/s (final velocity; negative because it is in the opposite direction)
Pf=0.70kg⋅(−3.5m/s)=−2.45kg m/s
The change in momentum (ΔP) is given by:
ΔP=Pf−Pi
ΔP=−2.45kg m/s−4.2kg m/s=−6.65kg m/s
The magnitude of the change in momentum is the absolute value of ΔP:
|ΔP|=|−6.65kg m/s|=6.65kg m/s
The magnitude of the change in linear momentum is:
6.65kg m/s
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (Single Correct Choice )47videos
CENTER OF MASS
- BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (More than One Correct Choice)5videos
CENTER OF MASS
- BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (Integer )4videos
CENTER OF MASS
- BOOK - RESNICK AND HALLIDAYCHAPTER - CAPACITANCEEXERCISE - PRACTICE QUESTION (INTEGER TYPE)3videos
CAPACITANCE
- BOOK - RESNICK AND HALLIDAYCHAPTER - CIRCUITSEXERCISE - Practice Questions (Integer Type)3videos
CIRCUITS
Similar Questions
An object of m kg with speed of ms−1 strikes a wall at an angle θ and rebounds at the same speed and same angle. Find the magnitude of change in the momentum of object.
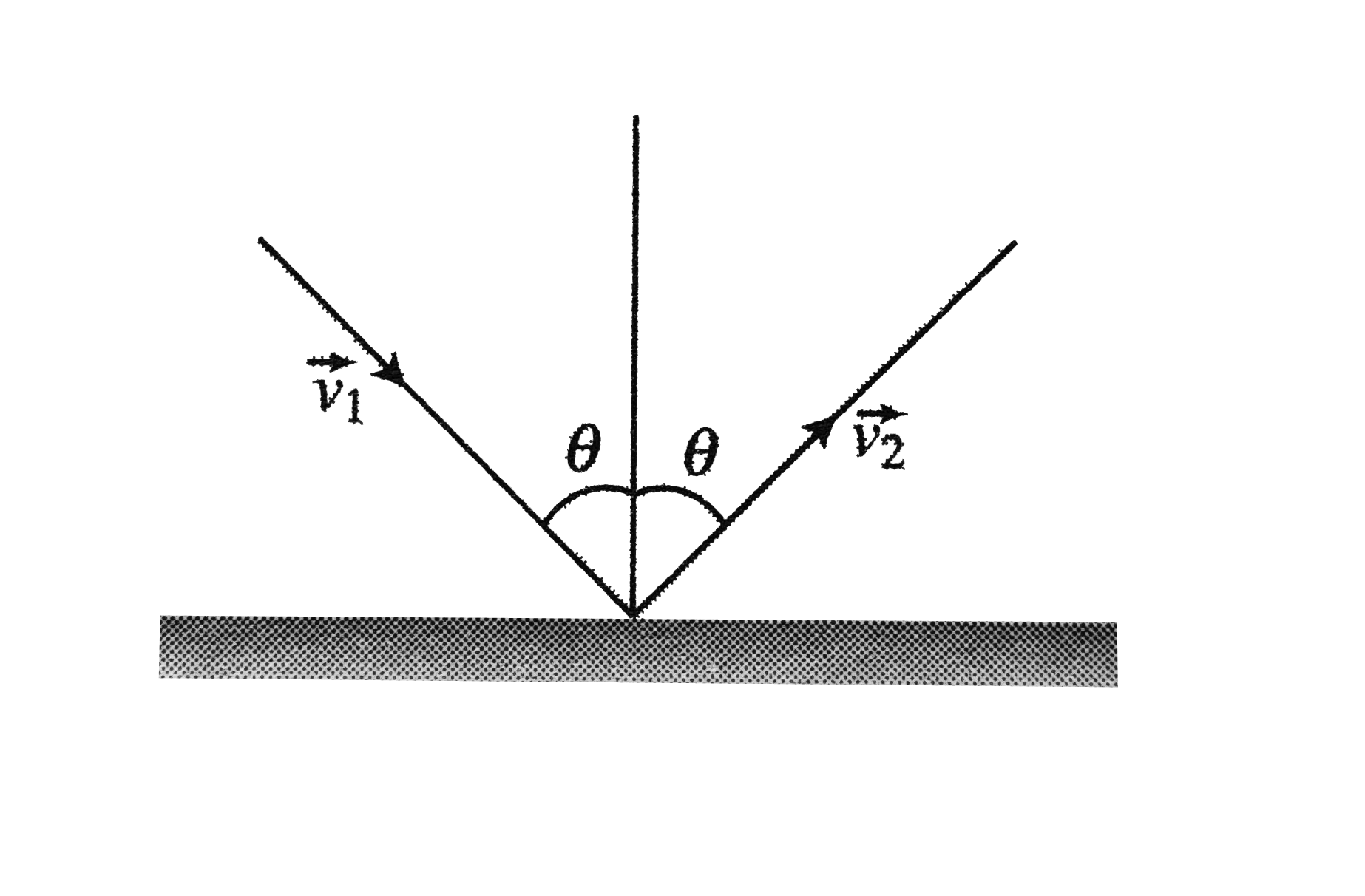 View Solution
View SolutionA ball moving with a momentum of 5kgms−1 strikes against a wall at an angle of 45∘ and is reflected at the same angle. Calculate the change in momentum.
View Solution
Knowledge Check
- Question 1 - Select One
A mass m with velocity u strikes a wall normally and returns with same speed. What is the magnitude of the change in momentum of the body when it returns.
A4 muBmuC2muDzero - Question 2 - Select One
A ball of mass 0⋅2 kg moving with a speed of 30 m/s strikes a bat returns in opposite direction with speed of 90m/s . Magnitude of change in momentu,m of ball will be
AZeroB6 kg m/sC12 kg m/sD24 kg m/s - Question 3 - Select One
A body falling with a speed of 2m/s strikes the floor and rebounds with a speed of 1 m/s. The loss of kinetic energy is
A12.5%B50%C25%D75%
A ball of mass 250 g moving with 20 m/s strikes a vertical wall and rebounds along the same line with a velocity of 15 m/s. If the time of contact is 0.1 s, the force exerted by the wall on the ball is
View SolutionA body of mass m collides against a wall with the velocity v and rebounds with the same speed. Its magnitude of change of momentum is
View SolutionA ball of mass 'm' strikes a rigid wall with speed 'u' and rebounds with the same speed. The impulse imparted to the ball by the wall is
View SolutionA ball of mass m strikes a rigid walJ with speed u and rebounds with the same speed. The impulse imparted to the ball by the wall is
View SolutionA ball of mass m strikes a rigid walJ with speed u and rebounds with the same speed. The impulse imparted to the ball by the wall is
 View Solution
View Solution

