A 1 kg block attached to a spring vibrates with a frequency of 1 Hz on a frictionless horizontal table. Two springs identical to the original spring are attached in parallel to an 8 kg block placed on the same table. So, the frequency of vibration of the 8 kg block is
2Hz
14Hz
12√2Hz
12Hz
The correct Answer is:A
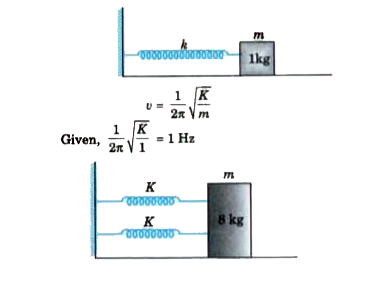 v.=12π√(K+K)M
v.=12π√(K+K)M
=12π√2K8
=12×1Hz
v.=12Hz
Topper's Solved these Questions
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Competition File (JEE (Advanced) For IIT Entrance)
7 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Competition File (Multiple choice question)
11 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Competition File (Multiple choice questions) AIPMT/NEET other State Boards for Medical Entrance
14 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST
16 Videos
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
Similar Questions
A block of mass 2kg is attached with a spring of spring constant 4000Nm−1 and the system is kept on smooth horizontal table. The other end of the spring is attached with a wall. Initially spring is stretched by 5cm from its natural position and the block is at rest. Now suddenly an impulse of 4kg−ms−1 is given to the block towards the wall.
Find the velocity of the block when spring acquires its natural length
View SolutionA block of mass 2kg is attached with a spring of spring constant 4000Nm−1 and the system is kept on smooth horizontal table. The other end of the spring is attached with a wall. Initially spring is stretched by 5cm from its natural position and the block is at rest. Now suddenly an impulse of 4kg−ms−1 is given to the block towards the wall.
Approximate distance travelled by the block when it comes to rest for a second time (not including the initial one) will be (Take √45=6.70)
View Solution
Knowledge Check
A block is placed on a frictionless horizontal table. The mass of the block is m and springs are attached on either side with force constants K1andK2 . If the block is displaced a little and left to oscillate, then the angular frequency of oscillation will be
A(K1+K2m)1/2B[K1+K2m(K1+K2)]1/2C[K1+K2(K1−K2)m]1/2D[K1K2(K1+K2)m]1/2A 1.0kg block oscillates with a frequency of 10Hz at the end of a certain spring. The spring is then cut into two halves. The 1.0kg block is then made to oscillate at the end of one of the halves. What is the frequency of oscillation of the block?
A5HzB10HzC14HzD20HzTwo spring are connected toa block of mass M placed a frictionless surface as shown if both the spring have a spring constant k the frequency of oscillation block is
 A12π√k2MB12π√kMC12π√2kMD12π√Mk
A12π√k2MB12π√kMC12π√2kMD12π√Mk
A block is attached to a horizontal spring and oscillates back and forth on f frictionless horizontal surface at a frequency of 3.00Hz. The amplitude of the motion is 5.08×10−2m. At the point where the block has its maximum speed, it suddenly splits into two identical parts, only one part remaining attached to the spring. What is the amplitude and the frequency of the simple harmonic motion that exists after the block splits?
View SolutionA mass of 1kg attached to the bottom of a spring has a certain frequency of vibration. The following mass has to be added to it in order to reduce the frequency by half :
View SolutionA mass of 1kg attached to the bottom of a spring has a certain frequency of vibration. The following mass has to be added to it in order to reduce the frequency by half :
View SolutionAssertion: A block of small m attached to a stiff spring will have large oscillation frequency.
Reason: Stiff springs have high value of spring constant.
View SolutionA block of mss m is placed on a level frictionless table. The block is attached to a horizontally aligned spring fixed with its other end and is vibrating in a horizontal with the pariod T. Suddenly at the instant of time when the spring comes to the position of euilibrium and becomes unstretched the block disconnects form the spring and continues sliding across the frictionless surface away from the until it encounters loop of radius R. What must be the amplitude of vibrations of the block s on the spring in order for the block to complets one loop without falling down?
_E01_049_Q01.png)
View Solution
