A 10 g bullet travelling at 200 m/s strikes and remains embedded in a 2 kg target which is originally at rest but free to move. At what speed does the target move off ?
The correct Answer is:0.99 m/s
To solve the problem of a bullet embedding itself in a target, we can use the principle of conservation of momentum. Here’s a step-by-step solution:
Step 1: Convert the mass of the bullet to kilograms
The mass of the bullet is given as 10 grams. To convert grams to kilograms:
Mass of bullet=10g=101000kg=0.01kg
Step 2: Identify the mass of the target
The mass of the target is given as 2 kg.
Step 3: Calculate the initial momentum before the collision
The bullet is moving at a velocity of 200 m/s, and the target is at rest (velocity = 0 m/s). The initial momentum (p_initial) can be calculated as:
pinitial=mass of bullet×velocity of bullet+mass of target×velocity of target
pinitial=(0.01kg×200m/s)+(2kg×0m/s)=2kg m/s
Step 4: Calculate the total mass after the collision
After the bullet embeds itself in the target, the total mass (m_total) of the system is:
mtotal=mass of bullet+mass of target=0.01kg+2kg=2.01kg
Step 5: Set up the equation for momentum after the collision
Let v be the common velocity of the bullet and the target after the collision. The momentum after the collision (p_final) is:
pfinal=mtotal×v=2.01kg×v
Step 6: Apply the law of conservation of momentum
According to the law of conservation of momentum:
pinitial=pfinal
Substituting the values we have:
2kg m/s=2.01kg×v
Step 7: Solve for v
Rearranging the equation to solve for v:
v=2kg m/s2.01kg≈0.99m/s
Final Answer
The speed at which the target moves off after the bullet embeds itself is approximately 0.99 m/s.
---
The mass of the bullet is given as 10 grams. To convert grams to kilograms:
Mass of bullet=10g=101000kg=0.01kg
The mass of the target is given as 2 kg.
The bullet is moving at a velocity of 200 m/s, and the target is at rest (velocity = 0 m/s). The initial momentum (p_initial) can be calculated as:
pinitial=mass of bullet×velocity of bullet+mass of target×velocity of target
pinitial=(0.01kg×200m/s)+(2kg×0m/s)=2kg m/s
After the bullet embeds itself in the target, the total mass (m_total) of the system is:
mtotal=mass of bullet+mass of target=0.01kg+2kg=2.01kg
Let v be the common velocity of the bullet and the target after the collision. The momentum after the collision (p_final) is:
pfinal=mtotal×v=2.01kg×v
According to the law of conservation of momentum:
pinitial=pfinal
Substituting the values we have:
2kg m/s=2.01kg×v
Rearranging the equation to solve for v:
v=2kg m/s2.01kg≈0.99m/s
The speed at which the target moves off after the bullet embeds itself is approximately 0.99 m/s.
Topper's Solved these Questions
Similar Questions
A 10 g bullet moving at 200 m/s stops after penetrating 5 cm of wooden plank. The average force exerted on the bullet will be
View SolutionA 5.20 g bullet moving at 700 m/s strikes a 700 g wooden block at rest on a frictionless surface. The bullet emerges, traveling in the same direction with its speed reduced to 450 m/s. (a) What is the resulting speed of the block? (b) What is the speed of the bullet-block center of mass ?
View Solution
Knowledge Check
A 10.0-g bullet traveling horizontally at 755 m/s strikes a stationary target and stops after penetrating 14.5 cm into the target. What is the average force of the target on the bullet ?
A1.97×104NB6.26×103NC2.07×105ND3.13×104NA 10 g bullet moving at 200 m/s stops after penetrating 5 cm of wooden plank. The average force exerted by the bullet will be
A2000NB−2000NC4000ND−4000NIn the given diagram a 0.1 kg bullet moving with speed 20 m/sec strikes 1.9kg mass and get embedded in it. find the kinetic energy of the mass with which it will strikes the ground is
 A11 JB21JC25JD30J
A11 JB21JC25JD30J
A bullet of mass 0.01 kg travelling at a speed of 500 m/s strikes a block of mass 2 kg, which is suspended by a string of length 5 m. The centre of gravity of the block is found to rise a vertical distance of 0.1 m. The speed of the bullet after it emerges from the block will be -
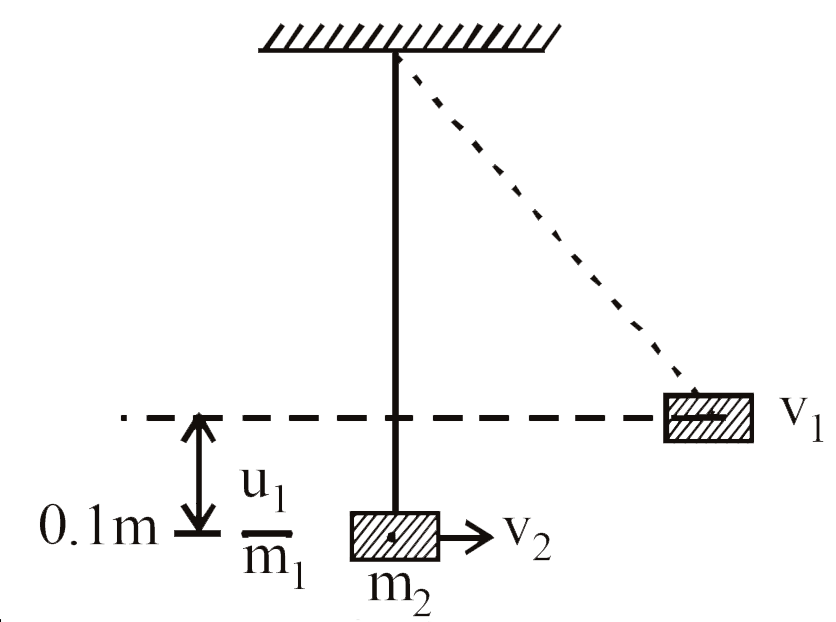
View SolutionA 50 g bullet moving with velocity 10 m / s strikes a block of mass 950 g at rest and gets embedded in it. The loss in kinetic energy will be
View SolutionA bullet of mass m travelling with a speed v hits a block of mass M initially at rest and gets embedded in it. The combined system is free to move and there is no other force acting on the system. The heat generated in the process will be
View SolutionA bullet of mass in travelling with a speed v hits a block of mass M initially at rest and gets embedded in it. The combined system is free to move and there is no other force acting on the system. The heat generated in the process will be
View SolutionA 50 g bullet moving with velocity 10 m / s strikes a block of mass 950 g at rest and gets embedded in it. The loss in kinetic energy will be
View Solution
