A 10 kg body is suspended by a rope is pulled by means of a horizontal force to make 60° by rope to vertical. The horizontal force is
10 kgwt
30 kgwt
10√3 kgwt
30√3 kgwt
The correct Answer is:C
To solve the problem, we will analyze the forces acting on the body suspended by the rope and apply the principles of equilibrium.
1. Identify the Forces Acting on the Body:
- The weight of the body (W) acting downwards: W=mg where m=10kg and g=9.8m/s2.
- The tension (T) in the rope acting at an angle of 60° to the vertical.
- A horizontal force (F) acting to pull the body.
2. Calculate the Weight of the Body:
W=mg=10kg×9.8m/s2=98N
3. Resolve the Tension into Components:
- The tension can be resolved into two components:
- Vertical component: Tv=Tcos(60°)
- Horizontal component: Th=Tsin(60°)
Knowing that cos(60°)=12 and sin(60°)=√32:
Tv=T⋅12=T2
Th=T⋅√32
4. Apply the Equilibrium Condition in the Vertical Direction:
Since the body is in equilibrium, the vertical component of tension must balance the weight of the body:
Tv=W
T2=98N
5. Solve for Tension (T):
T=98N×2=196N
6. Apply the Equilibrium Condition in the Horizontal Direction:
The horizontal force (F) must balance the horizontal component of the tension:
F=Th
F=T⋅√32
7. Substitute the Value of T:
F=196N⋅√32
F=98√3N
Final Answer:
The horizontal force F required to maintain the angle of 60° with the vertical is:
F=98√3N
- The weight of the body (W) acting downwards: W=mg where m=10kg and g=9.8m/s2.
- The tension (T) in the rope acting at an angle of 60° to the vertical.
- A horizontal force (F) acting to pull the body.
W=mg=10kg×9.8m/s2=98N
- The tension can be resolved into two components:
- Vertical component: Tv=Tcos(60°)
- Horizontal component: Th=Tsin(60°)
Tv=T⋅12=T2
Th=T⋅√32
Since the body is in equilibrium, the vertical component of tension must balance the weight of the body:
Tv=W
T2=98N
T=98N×2=196N
The horizontal force (F) must balance the horizontal component of the tension:
F=Th
F=T⋅√32
F=196N⋅√32
F=98√3N
The horizontal force F required to maintain the angle of 60° with the vertical is:
F=98√3N
Similar Questions
A body of mass 10 kg is suspended by a string and is pulled a side with a horizontal force of 49 N. Find the tension in the string, if the body is in equilibrium under these forces.
View SolutionA body of weight W is suspended by a string It is pulled aside with a horizontal force of 2W and held at rest. The tension in it is
View Solution
Knowledge Check
A block fof mass 5kg is suspended by a massless rope of length 2 m from the ceilling. A force of 50 N is applied in the horizontal direction at the midpoint P of the rope, as shown in the figure. The angle made by the rope with the vertical in equilibrium is (Take g=10ms−2m .
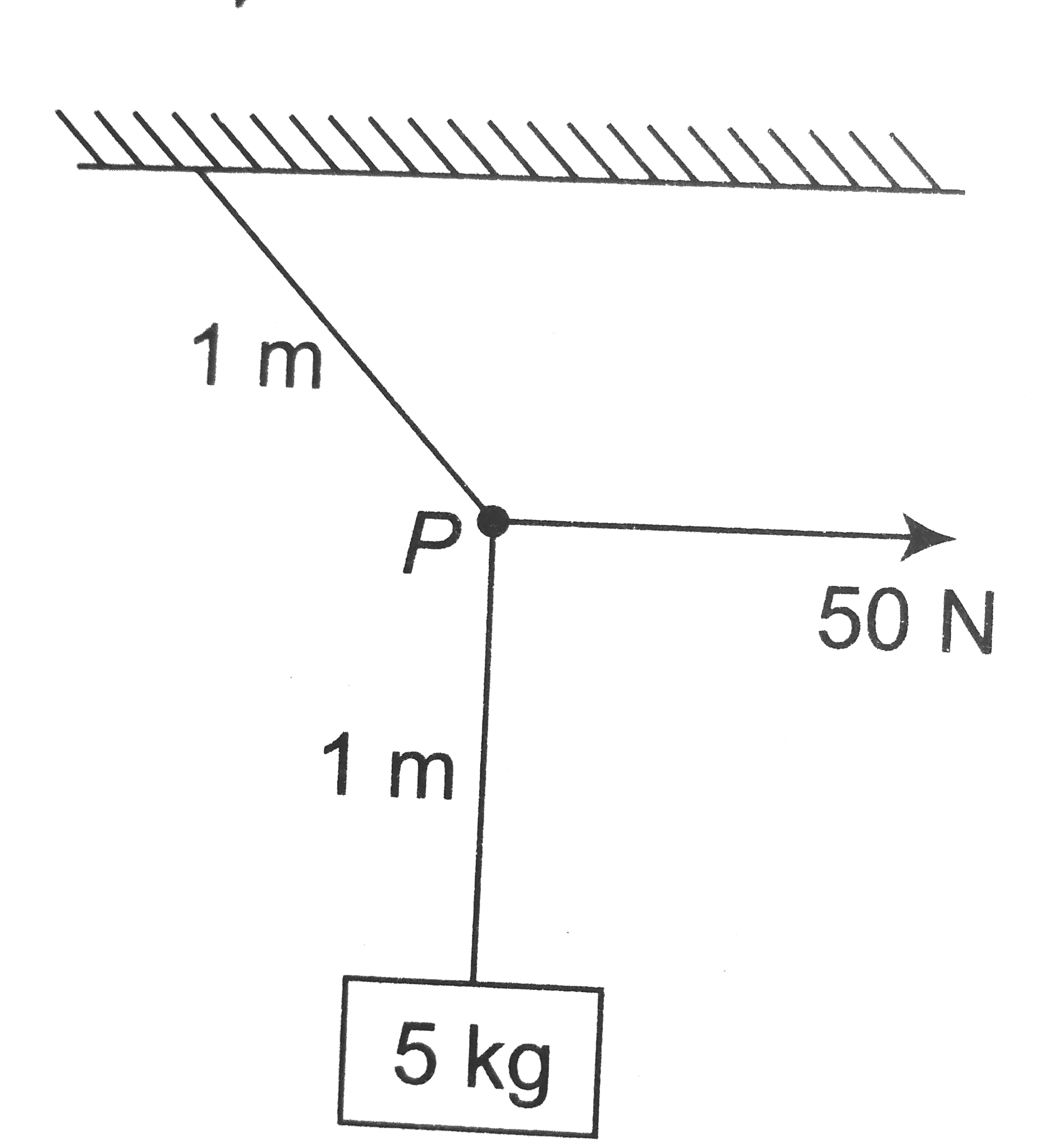 A30∘B40∘C60∘D45∘
A30∘B40∘C60∘D45∘
A mass of 10 kg is suspended vertically by a rope from the roof. When a horizontal force is applied on the rope at some point, the rope deviated at an angle of 45∘ at the roof point. If the suspended mass is at equilibrium, the magnitude of the force applied is (g=10ms−2)
View SolutionA mass of 10 kg is suspended vertically by a rope from the roof. When a horizontal force is applied on the rope at some point, the rope deviated at an angle of 45∘ at the roof point. If the suspended mass is at equilibrium, the magnitude of the force applied is (g=10ms−2)
View SolutionA block of mass M is pulled along a horizontal frictionless surface by a rope of mass m as shown in A horizontal force F is applied to one end of the rope. Find
(a) the acceleration of the rope and block
(b) the force that the rope exerts on the block
(c) the tension in the rope at its mid point

View SolutionA body of mass M is kept on a rough horizontal surface (friction coefficient =μ). A person is trying to pull the body by applying a horizontal force but the body is not moving. The force by the horizontal surface on the surface of the body is F, where
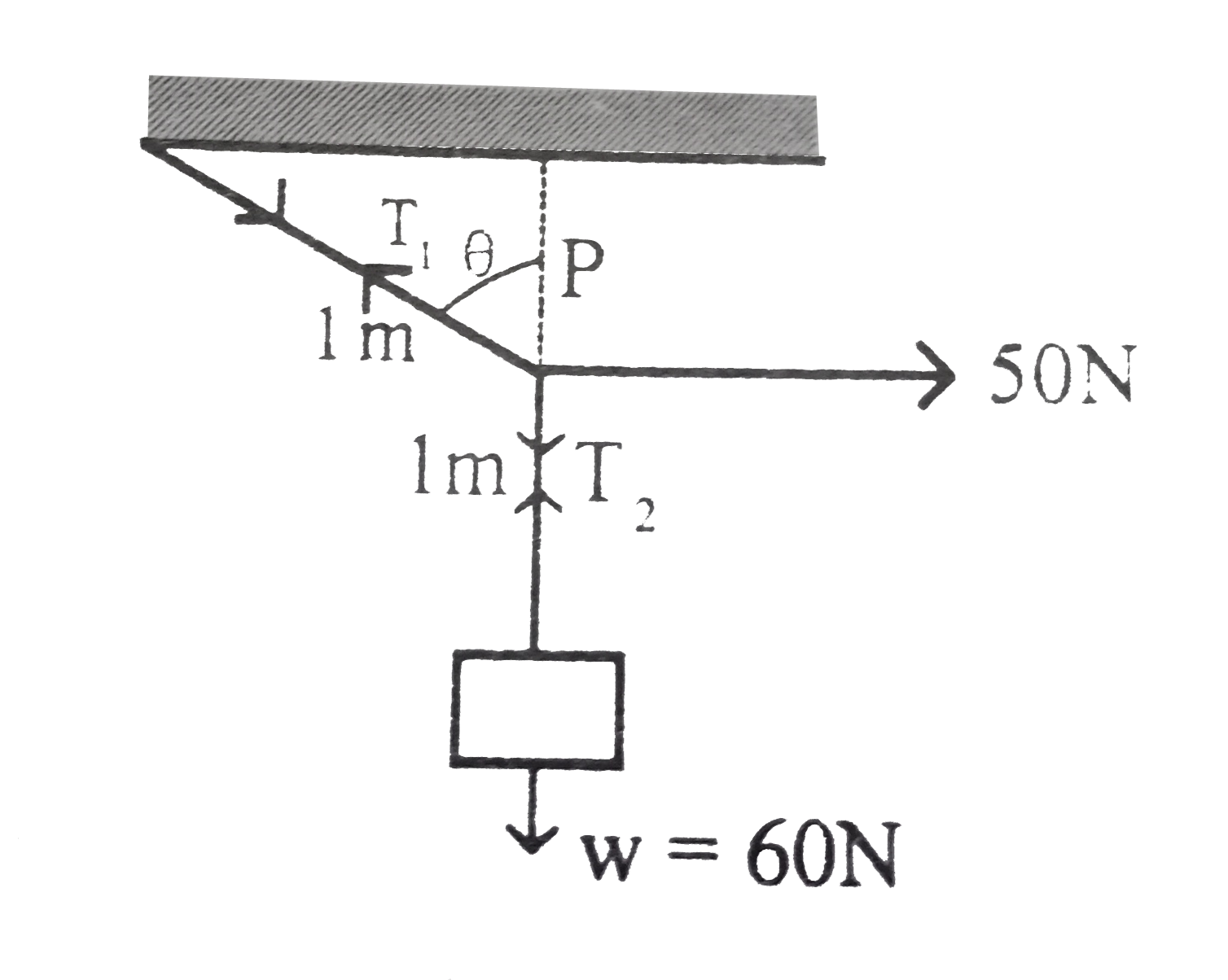
View SolutionA mass of 6 kg is suspended by a rope of length 2 m from the ceilling A force of 50 N in the horizontal direction is applied at the mid - point P of the rope as shown . What is the angle the rope makes with the vertical in equilibrium ? (Take = 10ms−2) . Neglect mass of the rope .
View SolutionA mass of 6 kg is suspended by a rope of length 2m from a celling. A force of 50N is applied in horizontal direction at the mid point of the rope. What is the angle of the rope with the verticle in equilibrium:-
View SolutionA weight w is suspended from the midpoint of a rope, whose ends are at the same level. In order to make the rope perfectly horizontal, the force applied to each of its ends must be
View Solution
