A mass of 10 kg is suspended vertically by a rope from the roof. When a horizontal force is applied on the rope at some point, the rope deviated at an angle of 45∘ at the roof point. If the suspended mass is at equilibrium, the magnitude of the force applied is (g=10ms−2)
70 N
75 N
100 N
90 N
The correct Answer is:C
To solve the problem, we need to analyze the forces acting on the mass and the rope when a horizontal force is applied, causing the rope to deviate at an angle of 45 degrees.
1. Identify the Forces:
- The weight of the mass (W) acting downward:
W=mg=10kg×10m/s2=100N
- The tension (T) in the rope acting at an angle of 45 degrees from the vertical.
- The horizontal force (F) applied to the rope.
2. Draw a Free Body Diagram:
- At the point where the rope is attached to the roof, the tension T can be resolved into two components:
- Vertical component: Tcos(45∘)
- Horizontal component: Tsin(45∘)
3. Set Up the Equilibrium Conditions:
- Since the mass is in equilibrium, the sum of the vertical forces must equal zero:
Tcos(45∘)=mg
- The sum of the horizontal forces must also equal zero:
Tsin(45∘)=F
4. Substituting Values:
- From the vertical equilibrium condition:
Tcos(45∘)=100N
Since cos(45∘)=1√2:
T⋅1√2=100⟹T=100√2N
5. Finding the Horizontal Force:
- Now substitute T into the horizontal equilibrium condition:
Tsin(45∘)=F
Since sin(45∘)=1√2:
F=(100√2)⋅1√2=100N
6. Conclusion:
- The magnitude of the horizontal force applied is:
F=100N
Final Answer:
The magnitude of the force applied is 100 N.
- The weight of the mass (W) acting downward:
W=mg=10kg×10m/s2=100N
- The tension (T) in the rope acting at an angle of 45 degrees from the vertical.
- The horizontal force (F) applied to the rope.
- At the point where the rope is attached to the roof, the tension T can be resolved into two components:
- Vertical component: Tcos(45∘)
- Horizontal component: Tsin(45∘)
- Since the mass is in equilibrium, the sum of the vertical forces must equal zero:
Tcos(45∘)=mg
- The sum of the horizontal forces must also equal zero:
Tsin(45∘)=F
- From the vertical equilibrium condition:
Tcos(45∘)=100N
Since cos(45∘)=1√2:
T⋅1√2=100⟹T=100√2N
- Now substitute T into the horizontal equilibrium condition:
Tsin(45∘)=F
Since sin(45∘)=1√2:
F=(100√2)⋅1√2=100N
- The magnitude of the horizontal force applied is:
F=100N
The magnitude of the force applied is 100 N.
Topper's Solved these Questions
Similar Questions
A mass of 6 kg is suspended by a rope of length 2m from a celling. A force of 50N is applied in horizontal direction at the mid point of the rope. What is the angle of the rope with the verticle in equilibrium:-
View SolutionA 10 kg body is suspended by a rope is pulled by means of a horizontal force to make 60° by rope to vertical. The horizontal force is
View Solution
Knowledge Check
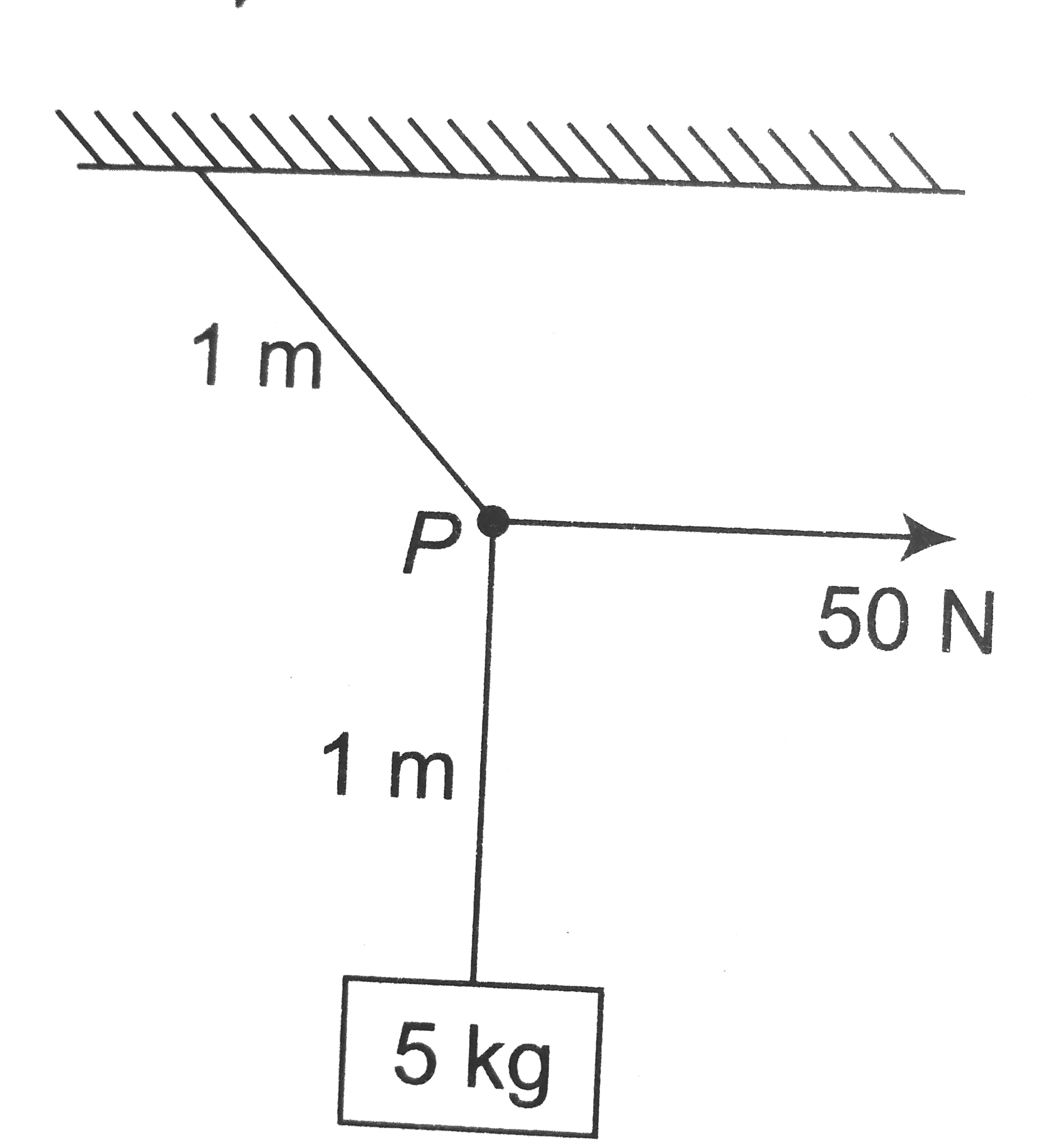
A block fof mass 5kg is suspended by a massless rope of length 2 m from the ceilling. A force of 50 N is applied in the horizontal direction at the midpoint P of the rope, as shown in the figure. The angle made by the rope with the vertical in equilibrium is (Take g=10ms−2m .
 A30∘B40∘C60∘D45∘
A30∘B40∘C60∘D45∘
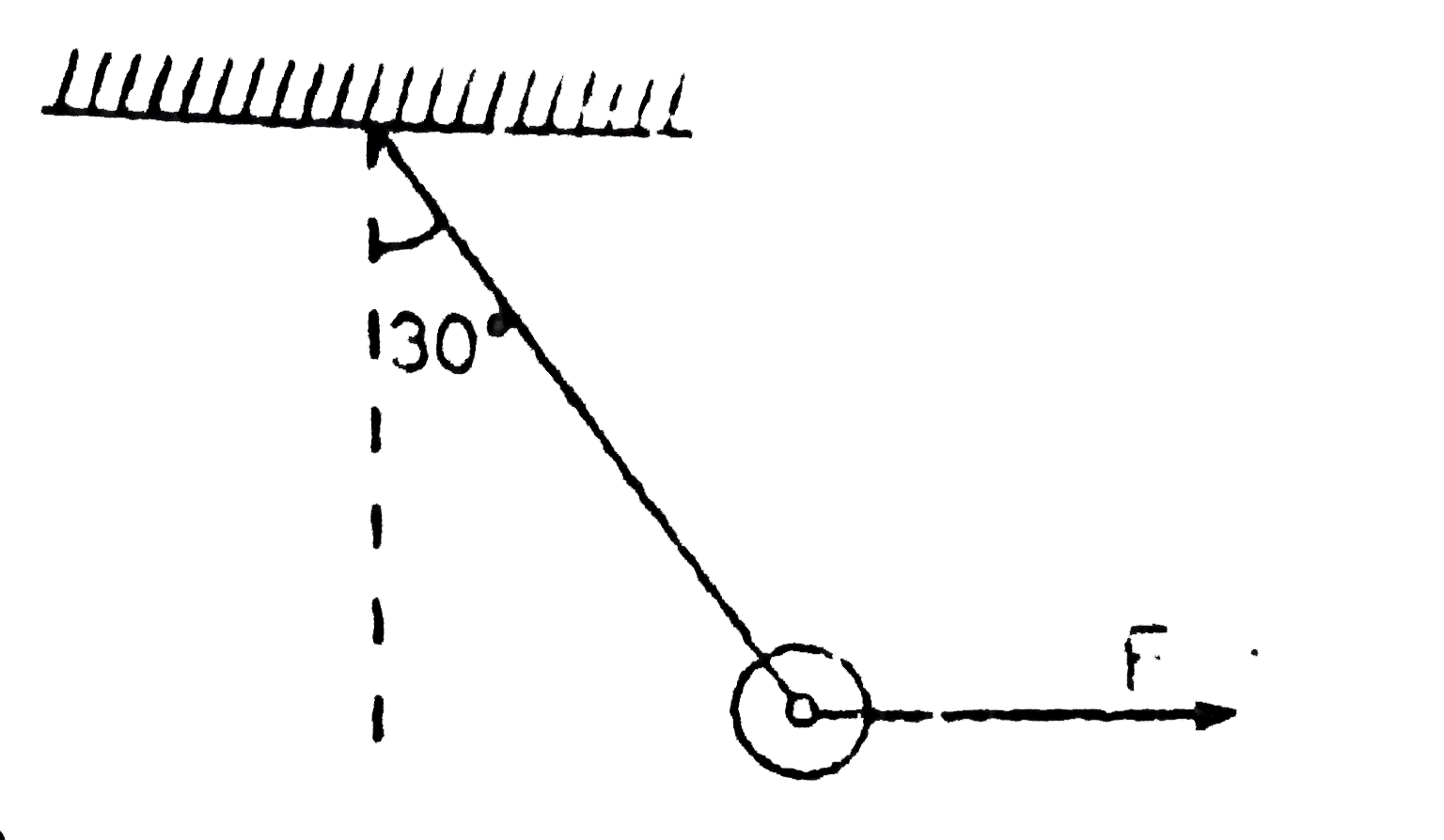
A heavy particle of mass 1kg suspended from a massless string attached to a roof. A horizontal force F is applied to the particle such that in the equilibrium position the string makes and angle 30∘ with the vertical. The magnitude of the force F equals
 .
.
View SolutionA mass of M kg is suspended by a weightless string. The horizontal force required to displace it until string makes an angle of 45∘ with the initial vertical direction is:
View SolutionA mass M kg is suspended by a weightless string. The horizontal force required to hold the mass at 60∘ with the vertical is
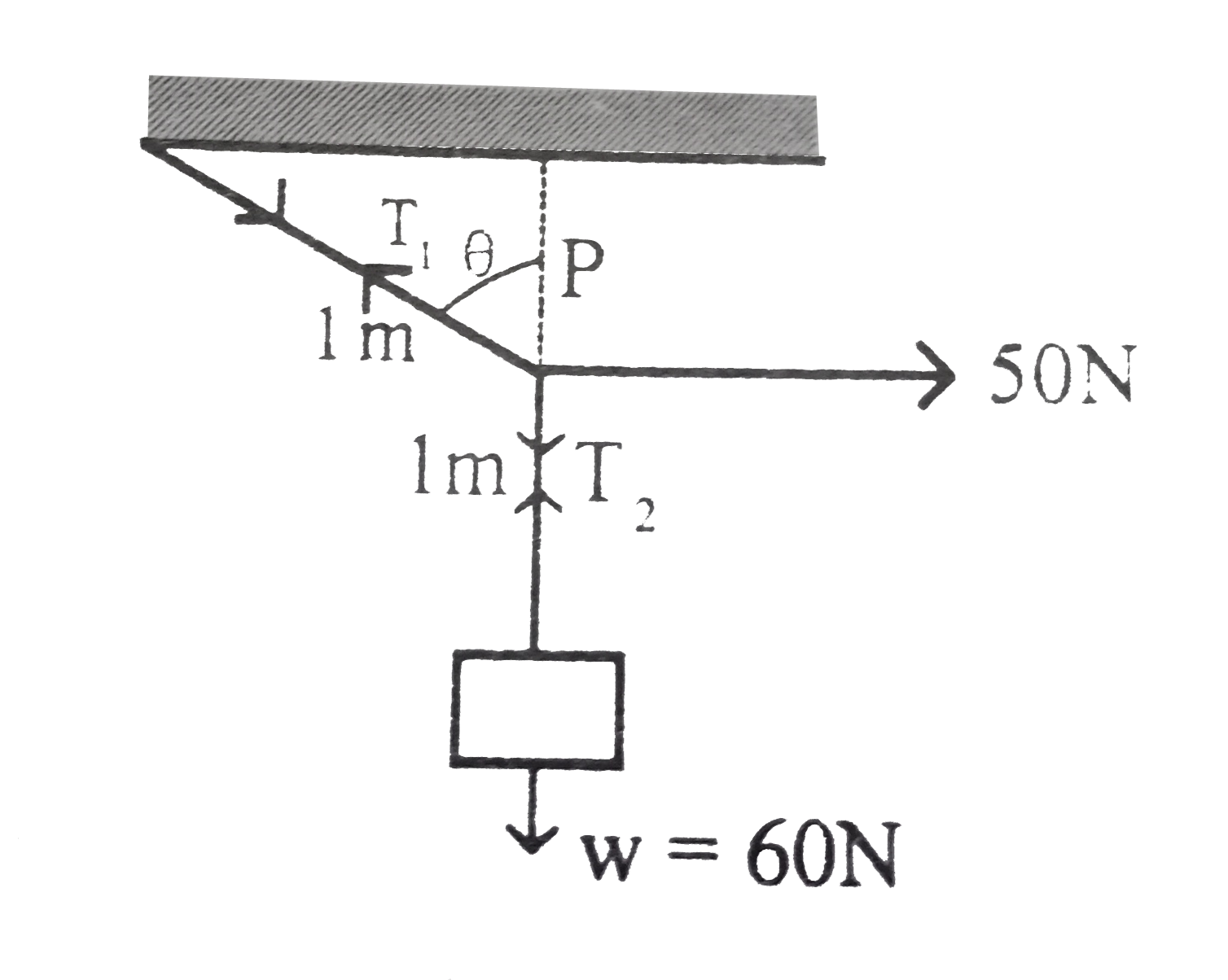
View SolutionSee Fig 5.8 .A mass of 6 kg is suspended by a rope of length 2m from the ceiling . A force of 50 N in the horizontal direction is applied at the mid-point P of the rope, as shown. What is the angle the rope makes with the vertical in equilibrium ? (Take g = 10 m s−2). Neglect the mass of the rope.
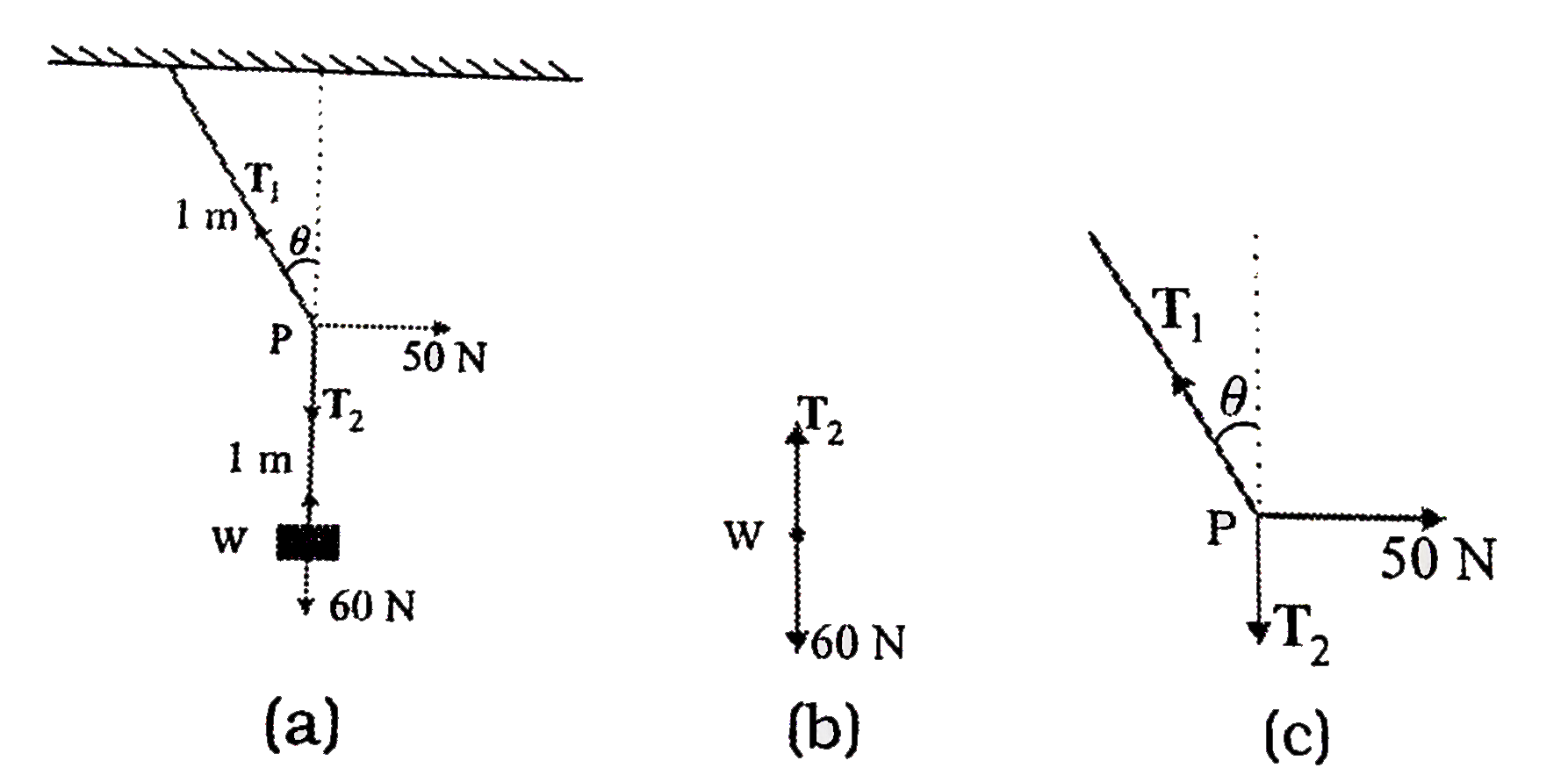
View SolutionA mass of 6 kg is suspended by a rope of length 2 m from the ceilling A force of 50 N in the horizontal direction is applied at the mid - point P of the rope as shown . What is the angle the rope makes with the vertical in equilibrium ? (Take = 10ms−2) . Neglect mass of the rope .
View Solution
A block of mass m is suspended from one end of a light spring as shown. The origin O is considered at distance equal to natural length of the spring from the ceiling and vertical downwards direction as positive y-axis. When the system is in equilibrium a bullet of mass m3 moving in vertical up wards direction with velocity v0 strikes the block and embeds into it. As a result, the block (with bullet embedded into it) moves up and start oscillating. Based on the given information, answer the following question:
Q. The time taken by the block bullet system to move from y=mgk (initial equilibrium position) to y=0 (natural length of spring) is (A represents the amplitude of motion)
View SolutionA block of mass Mis pulled vertically upward through a rope of mass m by applying force F on one end of the rope. What force does the rope exert on the block?
View Solution
