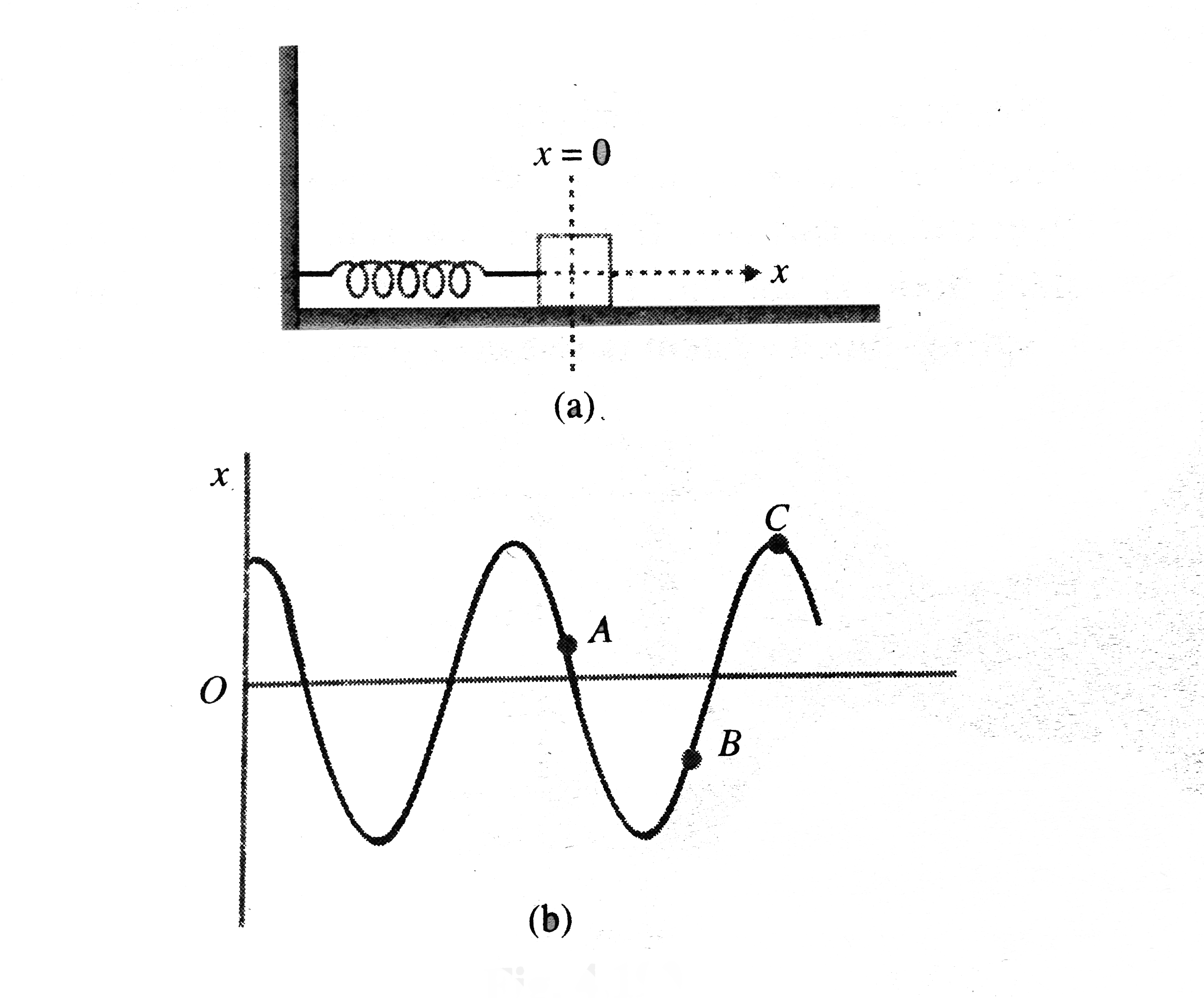
A 100 g block is connected to a horizontal massless spring of force constant 25.6Nm As shown in Fig. the block is free to oscillate on a horizontal frictionless surface. The block is displaced 3 cm from the equilibrium position and , at t=0, it is released from rest at x=0 It executes simple harmonic motion with the postive x-direction indecated in Fig. The position time (x−t) graph of motion of the block is as shown in Fig.
Position of the block as a function of time can now be expressed as
x=3cos(16t+π2)cm
x=3cos(16t+π3)cm
x=3.5cos(16t+π6)cm
x=3.2cos(16t+π4)cm
The correct Answer is:C
ω=√km=√25600100=16rads
Using energy conservation 12kx2+12mv2=12kA'2
A=√x2+mkv2=√9+3=2√3
x=Acos(ωt+ϕ)=2√3cos(16t+ϕ)
From boundary condition t=0 ϕ can be obtained which is π6.
x=2√3cos(16t+π6)cm
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Integer
10 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective type
2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reasoning
6 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
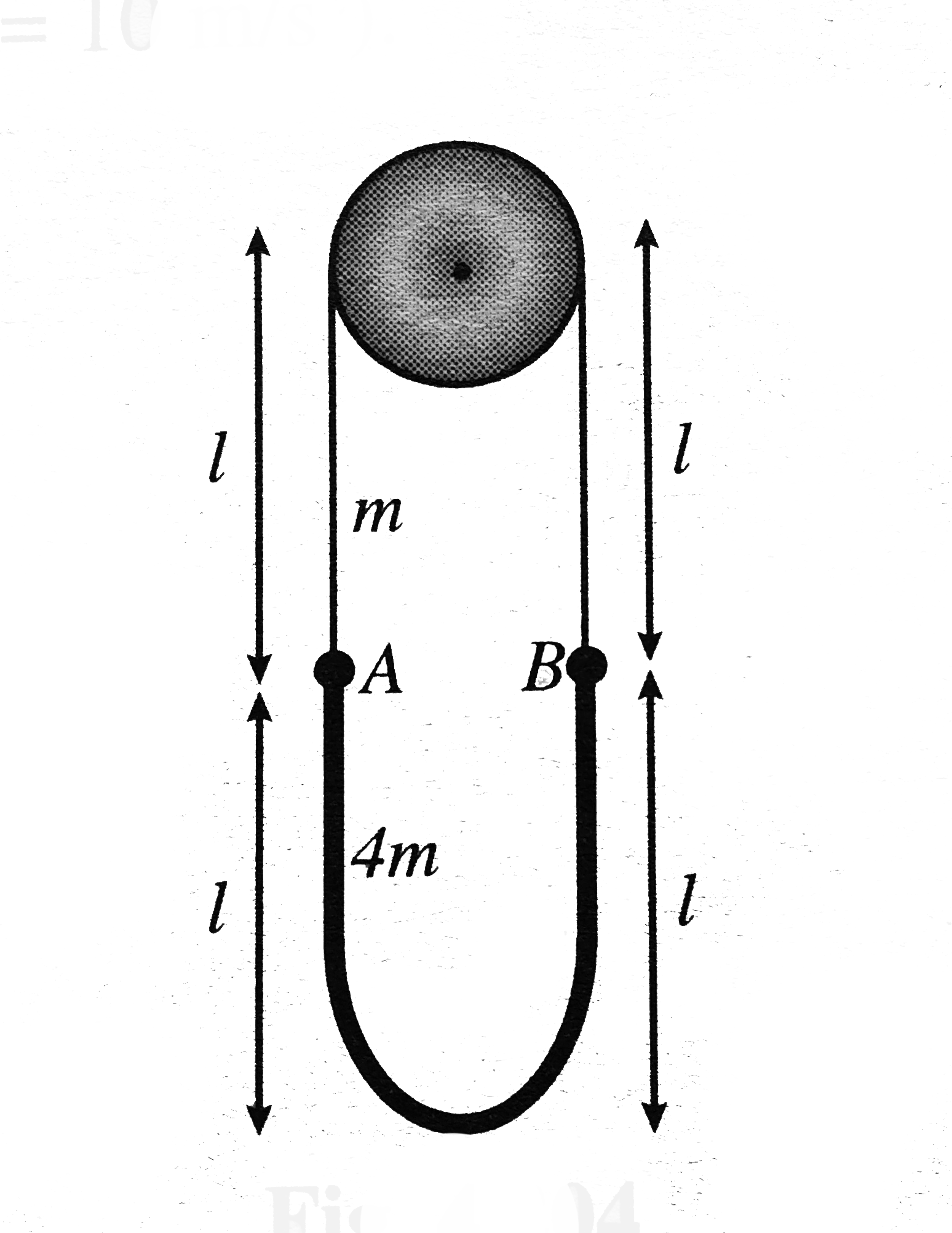
Two uniform ropes having linear mass densities m and 4m are joined to form a closed loop. The loop is hanging over a fixed frictionless small pulley with the lighter rope above as shown in the fig. (in the figure equilibrium position is shown). Now if point A (joint) is slightly displaced in downward direction and released, it is found that the loop performs SHM with the period of oscillation equal to N. Find the value of N (take l=150m4π2,g=10ms2).
View SolutionDescribe the motion of a particle acted upon by the force:
View SolutionQ. Statement I: The total energy of a particle performing simple harmonic motion could be negative. Statement II: Potential energy of a system could be magnetic.
View Solution8g of oxygen, 14 g of nitrogen and 22 g carbon dioxide are mixed in an encloser of volume 10 litre and temperature 27∘C. Calculate the pressure exerted by the mixture , R=8.3Jmole−1K−1, Molecular weight of oxygen , nitrogen and carbon 32 , 28 and 44 respectively.
View SolutionA train is moving along a straight line with a constant acceleration 'a' . A boy standing in the train throws a ball forward with a speed of 10m/s, at an angle of 60∘ to the horizontal. The boy has to move forward by 1.15m inside the train to catch the ball back at the initial height . the acceleration of the train , in m/s2 , is
View SolutionTwo blocks of equal mass m are connected by an unstretched spring and the system is kept at rest on a frictionless horizontal surface. A constant force F is applied on the first block pulling away from the other as shown in Fig. If the extension of the spring is x_(0) at time t , then the displacement of the second block at this instant is
View SolutionA 100 g block is connected to a horizontal massless spring of force constant 25.6(N)/(m) As shown in Fig. the block is free to oscillate on a horizontal frictionless surface. The block is displaced 3 cm from the equilibrium position and , at t=0 , it is released from rest at x=0 It executes simple harmonic motion with the postive x-direction indecated in Fig. The position time (x-t) graph of motion of the block is as shown in Fig. Q. When the block is at position A on the graph, its
View SolutionA 100 g block is connected to a horizontal massless spring of force constant 25.6(N)/(m) As shown in Fig. the block is free to oscillate on a horizontal frictionless surface. The block is displaced 3 cm from the equilibrium position and , at t=0 , it is released from rest at x=0 It executes simple harmonic motion with the postive x-direction indecated in Fig. The position time (x-t) graph of motion of the block is as shown in Fig. Q. When the block is at position B on the graph its.
View SolutionA 100 g block is connected to a horizontal massless spring of force constant 25.6(N)/(m) As shown in Fig. the block is free to oscillate on a horizontal frictionless surface. The block is displaced 3 cm from the equilibrium position and , at t=0 , it is released from rest at x=0 It executes simple harmonic motion with the postive x-direction indecated in Fig. The position time (x-t) graph of motion of the block is as shown in Fig. When the block is at position C on the graph, its
View SolutionA 100 g block is connected to a horizontal massless spring of force constant 25.6(N)/(m) As shown in Fig. the block is free to oscillate on a horizontal frictionless surface. The block is displaced 3 cm from the equilibrium position and , at t=0 , it is released from rest at x=0 It executes simple harmonic motion with the postive x-direction indecated in Fig. The position time (x-t) graph of motion of the block is as shown in Fig. Position of the block as a function of time can now be expressed as
View SolutionA 100 g block is connected to a horizontal massless spring of force constant 25.6(N)/(m) As shown in Fig. the block is free to oscillate on a horizontal frictionless surface. The block is displaced 3 cm from the equilibrium position and , at t=0 , it is released from rest at x=0 It executes simple harmonic motion with the postive x-direction indecated in Fig. The position time (x-t) graph of motion of the block is as shown in Fig. Velocity of the block as a function of time can be expressed as
View SolutionA 100g block is connected to a horizontal massless spring of force constant 25.6 N//m . The block is free to oscillate on a horizontal fricationless surface. The block is displced by 3 cm from the equilibrium position, and at t = 0 , it si released from rest at x = 0 , The position-time graph of motion of the block is shown in figure. When the block is at position A on the graph, its
View SolutionA 100g block is connected to a horizontal massless spring of force constant 25.6N/m. The block is free to oscillate on a horizontal fricationless surface. The block is displced by 3cm from the equilibrium position, and at t=0, it si released from rest at x=0, The position-time graph of motion of the block is shown in figure.
_S01_052_Q01.png)
Let us now make a slight change to the initial conditions. At t=0, let the block be released from the same position with an initial velocity v1=64cm/s. Position of the block as a function of time can be expressed as
View SolutionA block whose mass m is 680g is fastened to a spring whose spring constant k is 65N/m. The block is pulled a distance x=11cm from its equilibrium position at x=0 on a frictionless surface and released from rest at t= 0.
What is the displacement function x(t) for the spring block system?
View SolutionTwo blocks of equal mass m are connected by an unstretched spring and the system is kept at rest on a frictionless horizontal surface. A constant force F is applied on the first block pulling away from the other as shown in Fig. If the extension of the spring is x_(0) at time t , then the displacement of the first block at this instant is
View Solution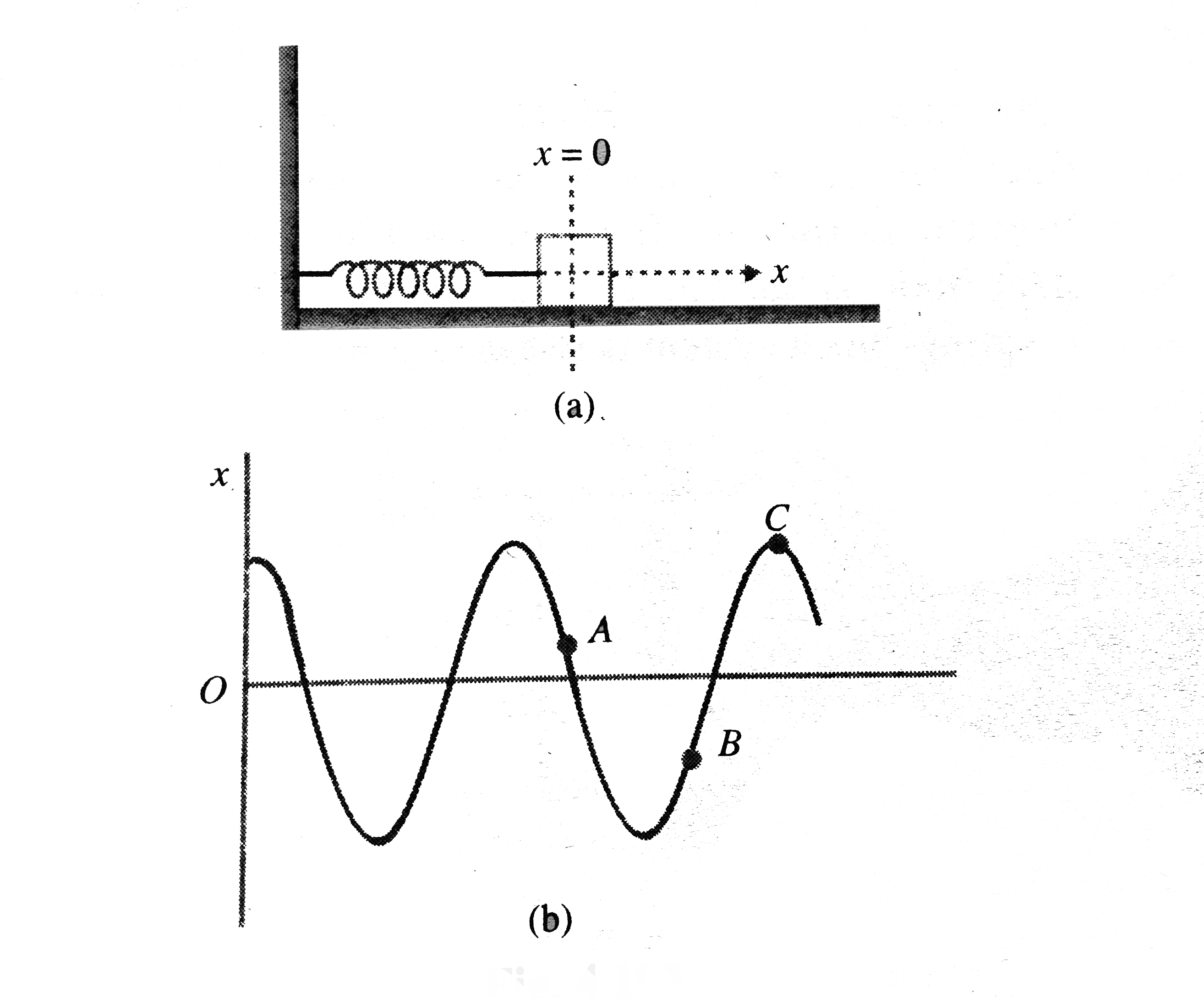
A 100 g block is connected to a horizontal massless spring of force constant 25.6Nm As shown in Fig. the block is free to oscillate on a horizontal frictionless surface. The block is displaced 3 cm from the equilibrium position and , at t=0, it is released from rest at x=0 It executes simple harmonic motion with the postive x-direction indecated in Fig. The position time (x−t) graph of motion of the block is as shown in Fig.
Velocity of the block as a function of time can be expressed as
View Solution
