A 5 kg collar is attached to a spring of spring constant 500 N m−1. It slides without friction over a horizontal rod. The collar is displaced from its equilibrium position by 10 cm and released. The time period of oscillation is
π5s
π2s
πs
2πs
The correct Answer is:A
To find the time period of oscillation for the collar attached to the spring, we can use the formula for the time period T of a mass-spring system:
T=2π√mk
where:
- T is the time period,
- m is the mass of the collar,
- k is the spring constant.
Step 1: Identify the given values
- Mass of the collar, m=5kg
- Spring constant, k=500N/m
Step 2: Substitute the values into the formula
Now, substituting the values of m and k into the formula:
T=2π√5kg500N/m
Step 3: Simplify the fraction inside the square root
Calculating the fraction:
5500=1100
Step 4: Take the square root
Now, taking the square root:
√1100=110
Step 5: Multiply by 2π
Now, substitute back into the equation for T:
T=2π⋅110=2π10=π5
Step 6: Conclusion
Thus, the time period of oscillation is:
T=π5seconds
Final Answer
The time period of oscillation is π5 seconds.
---
- T is the time period,
- m is the mass of the collar,
- k is the spring constant.
- Mass of the collar, m=5kg
- Spring constant, k=500N/m
Now, substituting the values of m and k into the formula:
Calculating the fraction:
Now, taking the square root:
Now, substitute back into the equation for T:
Thus, the time period of oscillation is:
The time period of oscillation is π5 seconds.
Topper's Solved these Questions
- OSCILLATIONS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Higher Order Thinking Skills
8 Videos
- OSCILLATIONS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Exemplar Problems
9 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - NCERT Exemplar
6 Videos
- PHYSICAL WORLDBOOK - NCERT FINGERTPS ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - Assertion And Reason
10 Videos
Similar Questions
A 5 kg collar is attached to a spring of spring constant 500Nm−1 . It slides without friction over a horizontal rod. The collar is displaced from its equilibrium position by 10 cm and released. Calculate (a) The period of oscillations (b) The maximum speed and (c) maximum acceleration of the collar.
View SolutionA 2.5 kg collar is attached to a spring of spring constant 250Nm−1 . It slides without friction over a horizontal surface . It is displaced from its equilibrium position by 20 cm and releasd. Calculate the period of osciallation and the maximum speed.
View SolutionA 2.5 kg collar attached to a spring of foce constant 1000 Nm−1 slides without friction on a horizontal rod. The collar is displaced from its equilibrium position by 5.0 cm and released. Calculate (i) the period of oscillation (ii) the maximum speed of the collar and (iii) the maximum acceleration of the collar.
View SolutionA 10 kg collar is attached to a spring of spring constant 1000Nm−1 . It slides without friction over a horizontal surface. If is displaced from its equilibrium position by 20 cm and released . Calculate
(a) The period of oscillation (b) The maximum speed
Hint :T=2π√mk,vm=Aω=A√km
View SolutionA 4 kg roller is attached to a massless spring of spring constant k = 100 N/m. It rolls without slipping along a frcitionless horizontal road. The roller is displaced from its equilibrium position by 10 cm and then released. It rolls without slipping along a frictionless horizontal road. The roller is displaced from its equilibrium position by 10 cm and then released. Its maximum speed will be
View SolutionA 5kg collar is attached to a spring . It slides without friction over a horizontal surface. It is displaced from its equilibrium position by 10 cm and released , its maximum speed is 1ms−1 Calculate
(a) Spring constant
(b) The period of oscillation
(c ) Maximum acceleration of the collar
Hint :m=5kg,A=0.1m,k=?,T=?or a=?,vm=1ms−1
vm=Aω=A√km
Find k,
T=2π√mk
amax=ω2A=kmA
View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10cm, then the period of oscillation is
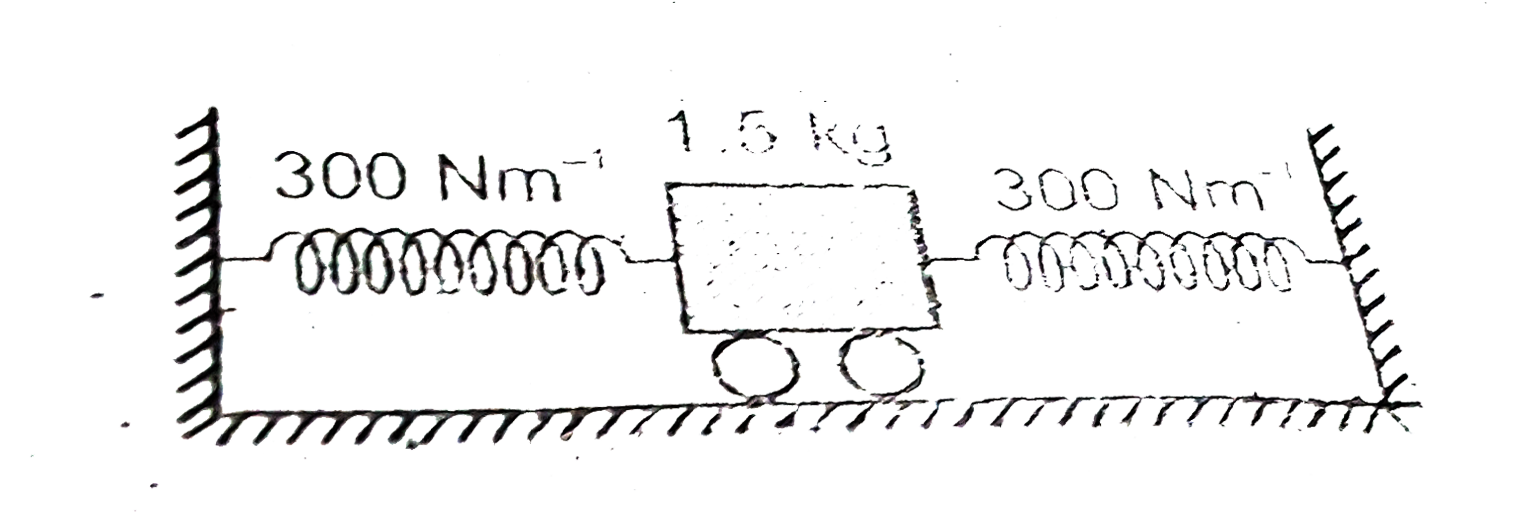
View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionA 10 kg metal block is attached to a spring constant 1000Nm−1. A block is displaced from equilibrium position by 10 cm and released. The maximum acceleration of the block is
View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10 cm, then maximum speed of the trolley is
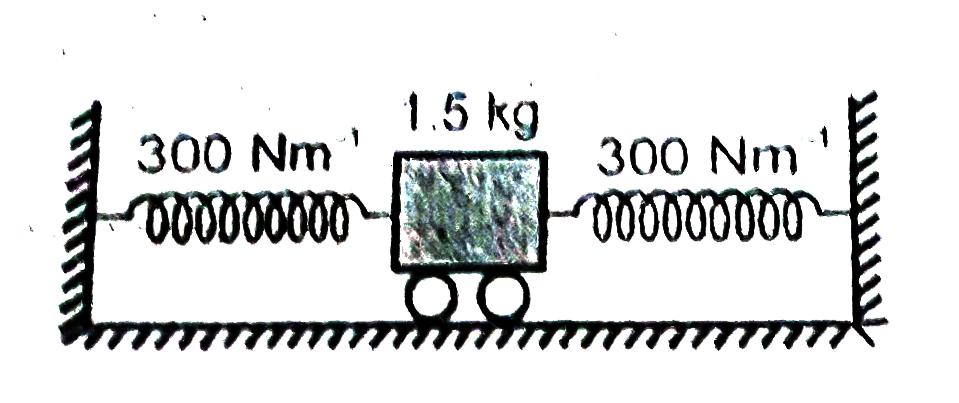
View Solution
