A 4 kg roller is attached to a massless spring of spring constant k = 100 N/m. It rolls without slipping along a frcitionless horizontal road. The roller is displaced from its equilibrium position by 10 cm and then released. It rolls without slipping along a frictionless horizontal road. The roller is displaced from its equilibrium position by 10 cm and then released. Its maximum speed will be
0.5ms−1
0.6ms−1
0.4ms−1
0.8ms−1
To find the maximum speed of the roller when it is displaced from its equilibrium position and then released, we can follow these steps:
1. Identify the Given Values:
- Mass of the roller, m=4kg
- Spring constant, k=100N/m
- Displacement from equilibrium, x=10cm=0.1m
2. Calculate the Potential Energy Stored in the Spring:
The potential energy (PE) stored in the spring when it is displaced from its equilibrium position is given by the formula:
PE=12kx2
Substituting the values:
PE=12×100N/m×(0.1m)2
PE=12×100×0.01=12J=0.5J
3. Apply the Conservation of Mechanical Energy:
When the roller is released, the potential energy will convert into kinetic energy (KE) at the equilibrium position. At the equilibrium position, the potential energy is zero, and all the energy is kinetic:
KE=12mv2
Setting the potential energy equal to the kinetic energy:
0.5J=12×4kg×v2
4. Solve for Maximum Speed v:
Rearranging the equation to solve for v2:
0.5=2v2⇒v2=0.52=0.25
Taking the square root to find v:
v=√0.25=0.5m/s
5. Conclusion:
The maximum speed of the roller when it reaches the equilibrium position is:
v=0.5m/s
- Mass of the roller, m=4kg
- Spring constant, k=100N/m
- Displacement from equilibrium, x=10cm=0.1m
The potential energy (PE) stored in the spring when it is displaced from its equilibrium position is given by the formula:
PE=12kx2
Substituting the values:
PE=12×100N/m×(0.1m)2
PE=12×100×0.01=12J=0.5J
When the roller is released, the potential energy will convert into kinetic energy (KE) at the equilibrium position. At the equilibrium position, the potential energy is zero, and all the energy is kinetic:
KE=12mv2
Setting the potential energy equal to the kinetic energy:
0.5J=12×4kg×v2
Rearranging the equation to solve for v2:
0.5=2v2⇒v2=0.52=0.25
Taking the square root to find v:
v=√0.25=0.5m/s
The maximum speed of the roller when it reaches the equilibrium position is:
v=0.5m/s
Similar Questions
A 5 kg collar is attached to a spring of spring constant 500Nm−1 . It slides without friction over a horizontal rod. The collar is displaced from its equilibrium position by 10 cm and released. Calculate (a) The period of oscillations (b) The maximum speed and (c) maximum acceleration of the collar.
View SolutionA 2.5 kg collar is attached to a spring of spring constant 250Nm−1 . It slides without friction over a horizontal surface . It is displaced from its equilibrium position by 20 cm and releasd. Calculate the period of osciallation and the maximum speed.
View Solution
Knowledge Check
A 5 kg collar is attached to a spring of spring constant 500 N m−1. It slides without friction over a horizontal rod. The collar is displaced from its equilibrium position by 10 cm and released. The time period of oscillation is
Aπ5sBπ2sCπsD2πs
A 2.5 kg collar attached to a spring of foce constant 1000 Nm−1 slides without friction on a horizontal rod. The collar is displaced from its equilibrium position by 5.0 cm and released. Calculate (i) the period of oscillation (ii) the maximum speed of the collar and (iii) the maximum acceleration of the collar.
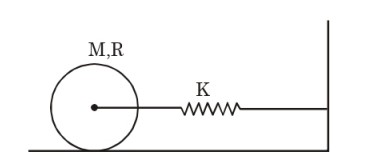
View SolutionFind the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.

View SolutionFind the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.

View SolutionA 10 kg collar is attached to a spring of spring constant 1000Nm−1 . It slides without friction over a horizontal surface. If is displaced from its equilibrium position by 20 cm and released . Calculate
(a) The period of oscillation (b) The maximum speed
Hint :T=2π√mk,vm=Aω=A√km
View SolutionA solid sphere of mass m is attached to a light spring of force constant k so that it can roll without slipping along a horizontal surface. Calculate the period of oscillation made by sphere.

View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10 cm, then maximum speed of the trolley is
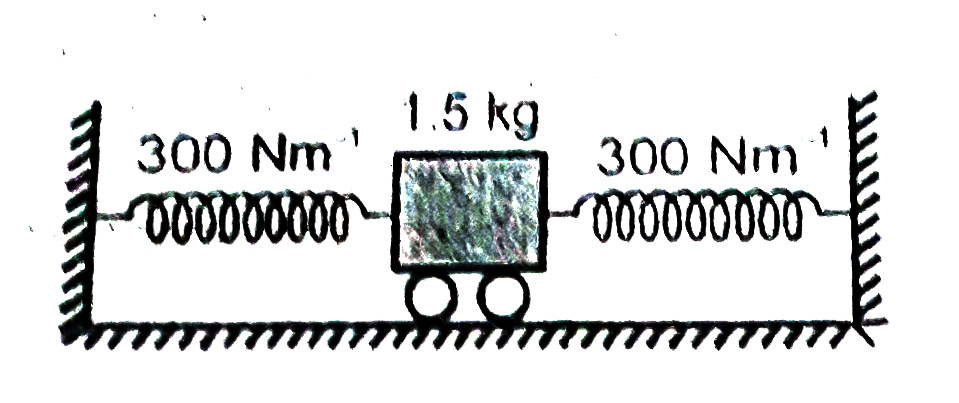
View SolutionA solid cylinder attached to horizontal massless spring can roll without slipping along a horizontal surface. Find time period of oscillation.
View Solution
