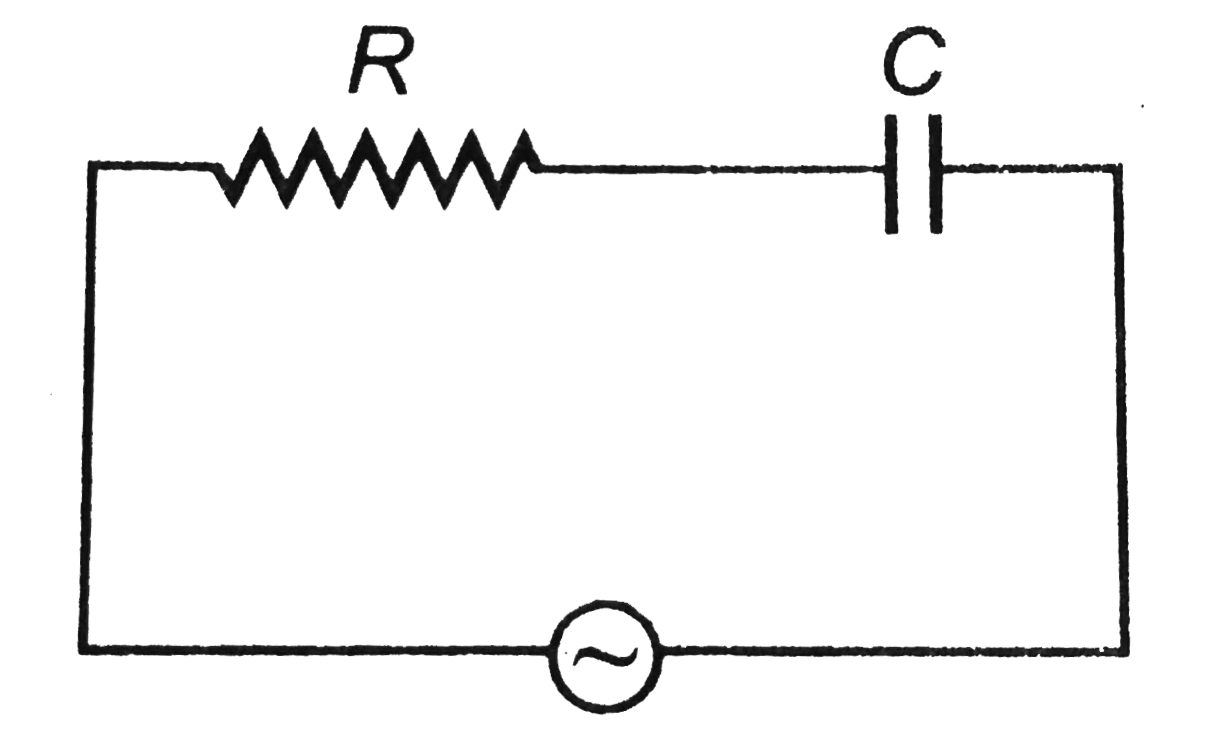
A 50HzAC source of 20V is connected across R and C as shown in figure.
The voltage across R is 12V. The voltage across C is
8V
16V
10V
not possible to determine unless value of R and C are given
The correct Answer is:B
VC=√V2−V2R=√(20)2−(12)2
=16V.
Topper's Solved these Questions
- ALTERNATING CURRENTBOOK - DC PANDEY ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Level - 1 Subjective
6 Videos
- ALTERNATING CURRENTBOOK - DC PANDEY ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Level- 2 Single Correct
18 Videos
- ALTERNATING CURRENTBOOK - DC PANDEY ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Level 1 Assertion-Reason
11 Videos
- ATOMSBOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY
42 Videos
Similar Questions
Knowledge Check
An ac source of voltage V=Vmsinωt is connected across the resistance R as shown in figure. The phase relation between current and voltage for this circuit is
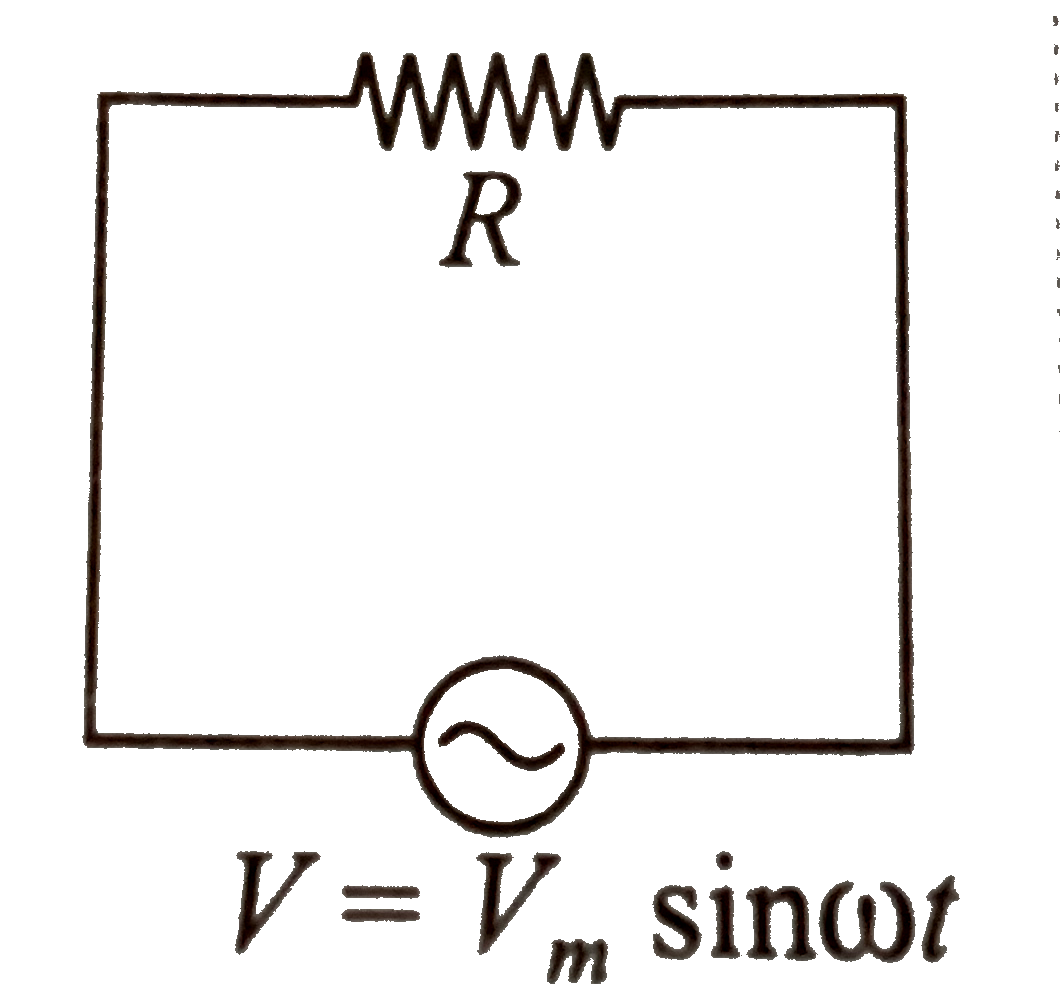 Aboth are in phaseBboth are out of phase by 90∘Cboth are out of phase by 120∘Dboth are out of phase by 180∘
Aboth are in phaseBboth are out of phase by 90∘Cboth are out of phase by 120∘Dboth are out of phase by 180∘
When an a.c source is connected across a resistor
View SolutionIn series LCR circuit, the voltages across R, L and C are shown in the figure. The voltage of applied source

View SolutionAn ac source of 50 V (r.m.s value) is connected across a series R - C circuit. If the r.m.s voltage across the resistor is 40 V, then the r.m.s voltage across the capacitor is
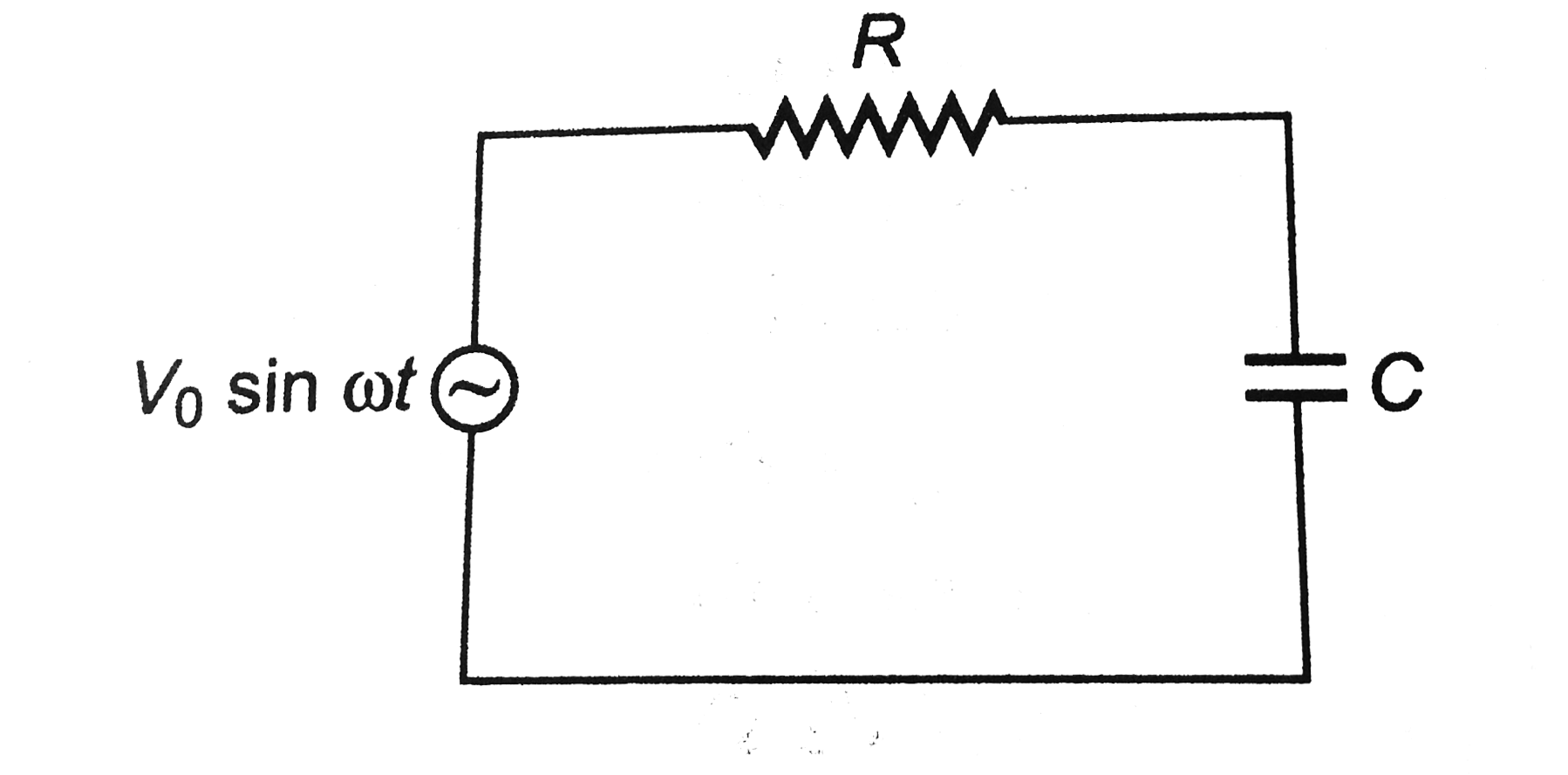
View SolutionAn AC voltage source V=V0siωtis connected across resistance R and capacitance C as shown in figureure. It is given that R=1ωC. The peak current is I0. If the angular frequency of the voltage source is changed to ω√3, then the new peak current in the circuit is
 .
.
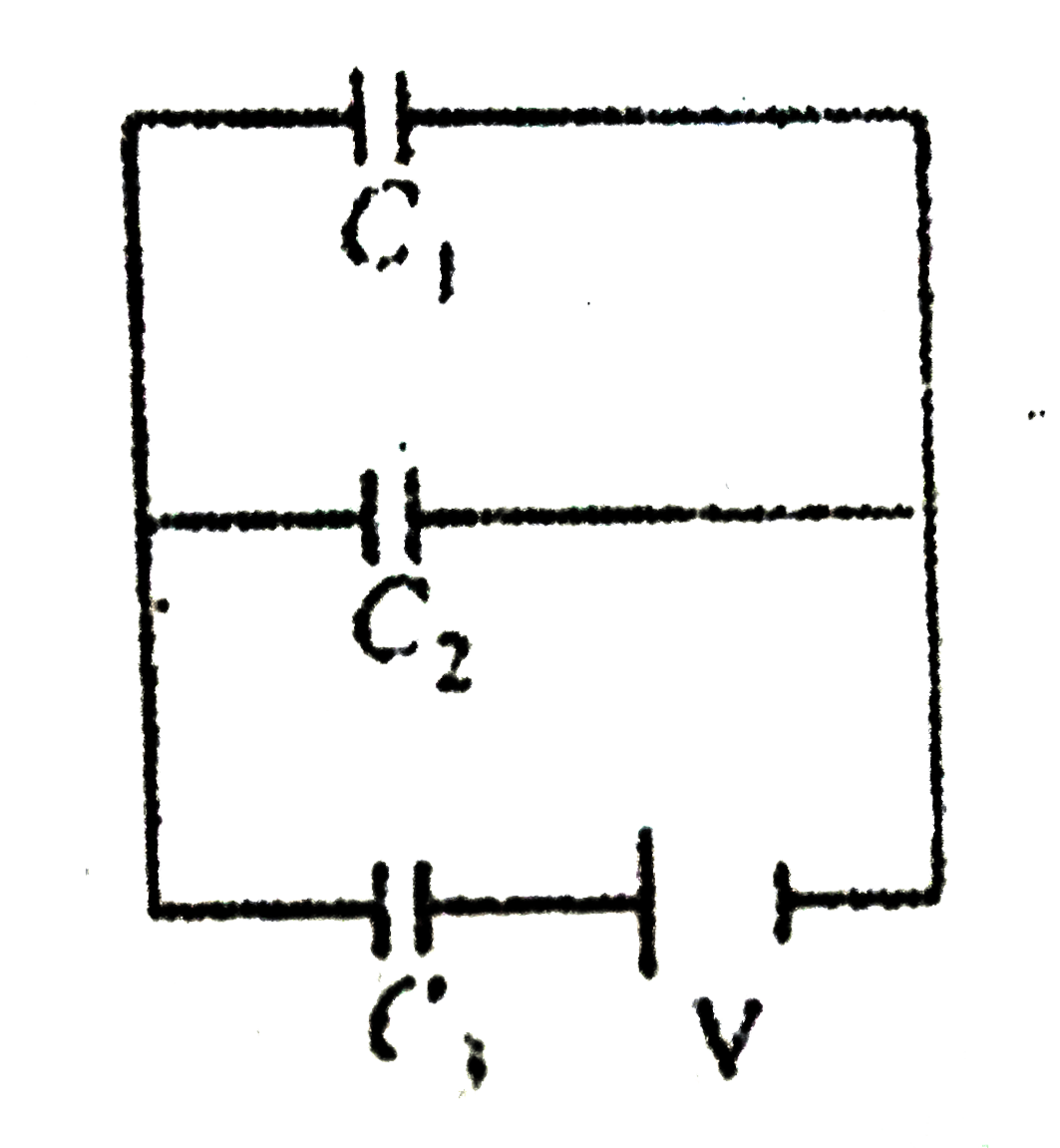
View SolutionWhat would be the voltage across C3?
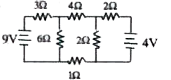
View SolutionFor the circuit shown in figure, determine the voltage across 4Ω resistors in volt ?
View SolutionAn AC voltage source V=V0sinωt is connected across resistance R and capacitance C as shown in figure. It is given that ωC=1R. The peak current is I0. If the angular frequency of the voltage source is changed to ω√3, then the new peak current in the circuit is
 .
.
View Solution