A steady current of magnitude I and an AC current of peak value I are allowed to pass through identical resistors for the same time. The ratio of heat produced in the two resistors will be
2:1
1:2
1:1
none of these
The correct Answer is:A
To solve the problem of finding the ratio of heat produced in two identical resistors when a steady current I and an AC current of peak value I0 are passed through them for the same time, we can follow these steps:
Step 1: Calculate Heat Produced by Steady Current (DC)
The heat produced in a resistor due to a steady current (DC) can be calculated using the formula:
HDC=I2Rt
where:
- HDC is the heat produced in the resistor,
- I is the steady current,
- R is the resistance,
- t is the time for which the current flows.
Step 2: Calculate Heat Produced by AC Current
For an alternating current (AC), we need to consider the root mean square (RMS) value of the current. The RMS value IRMS of an AC current with peak value I0 is given by:
IRMS=I0√2
The heat produced in the resistor due to the AC current can be calculated using the formula:
HAC=I2RMSRt
Substituting the RMS value into the equation, we get:
HAC=(I0√2)2Rt=I202Rt
Step 3: Find the Ratio of Heat Produced
Now, we can find the ratio of heat produced in the DC circuit to that produced in the AC circuit:
Ratio=HDCHAC=I2RtI202Rt
Notice that R and t cancel out:
Ratio=I2I202=2I2I20
Step 4: Substitute Peak Value
Since the problem states that the peak value of the AC current is equal to the steady current, we can substitute I0=I:
Ratio=2I2I2=2
Conclusion
Thus, the ratio of heat produced in the two resistors is:
Ratio=2:1
Final Answer
The ratio of heat produced in the two resistors is 2:1.
---
HDC=I2Rt
where:
- HDC is the heat produced in the resistor,
- I is the steady current,
- R is the resistance,
- t is the time for which the current flows.
IRMS=I0√2
HAC=I2RMSRt
Substituting the RMS value into the equation, we get:
HAC=(I0√2)2Rt=I202Rt
Ratio=HDCHAC=I2RtI202Rt
Ratio=I2I202=2I2I20
Ratio=2I2I2=2
Ratio=2:1
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Level - 1 Subjective6videos
ALTERNATING CURRENT
- BOOK - DC PANDEY ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Level- 2 Single Correct18videos
ALTERNATING CURRENT
- BOOK - DC PANDEY ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Level 1 Assertion-Reason11videos
ALTERNATING CURRENT
- BOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY42videos
ATOMS
Similar Questions
A direct current of 2 A and an alternating current having a maximum value of 2 A flow through two identical resistances. The ratio of heat produced in the two resistances will be
View SolutionA direct current of 2 A and an alternating current having a maximum value of 2 A flow through two identical resistances. The ratio of heat produced in the two resistances will be
View SolutionA direct current of 2 A and an alternating current having a maximum value of 2 A flow through two identical resistances. The ratio of heat produced in the two resistances will be
View SolutionThe value of current through 2Ω resistor is
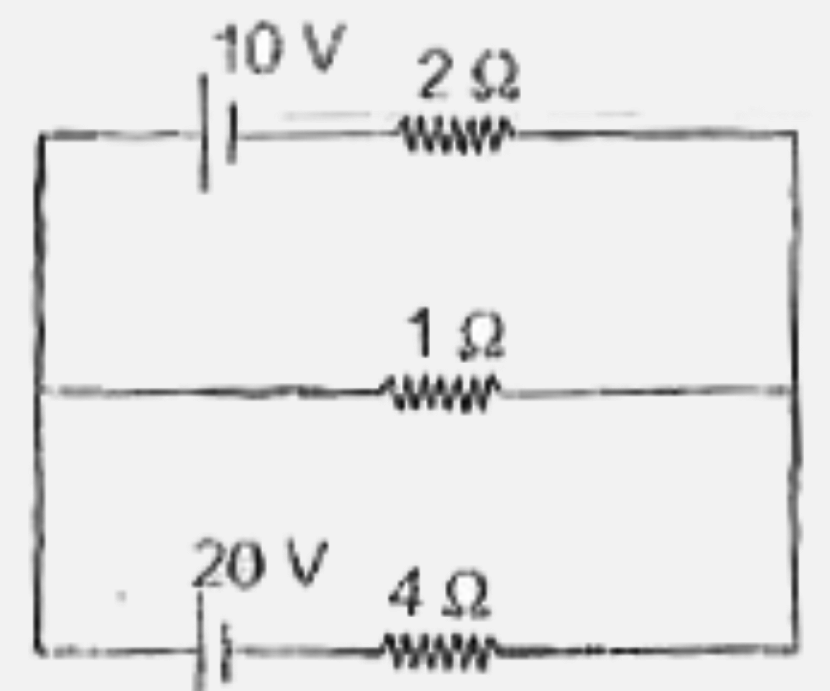 View Solution
View SolutionIn the figure given below, the current passing through 6Ω resistor is
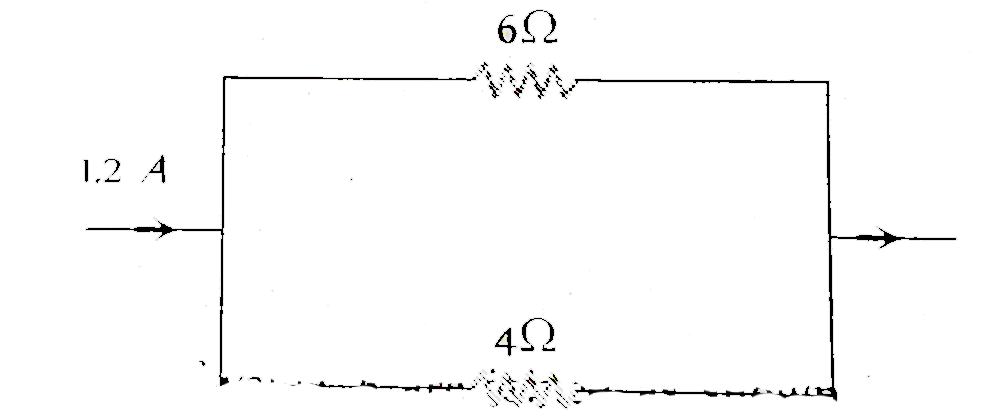 View Solution
View SolutionA sinusoidal alternating current of peak value (I0) passes through a heater of resistance R. What is the mean power output of the heater?
View SolutionThe same mass of copper is drawn into two wires 2 mm and 3mm thick. The two wires are connected in series and current is passed through them. The ratio of heat produced in the two wires is
View SolutionAn alternating current of rms value 10 A is passed through a 12Ω resistor. The maximum potential difference across the resistor is
View SolutionWhen a current passes through a resistor, its temperature increases. Is it an adiabatic process?
View SolutionA variable current flows through a 1Ω resistor for 2 s. Time dependence of the current is shown in the graph.
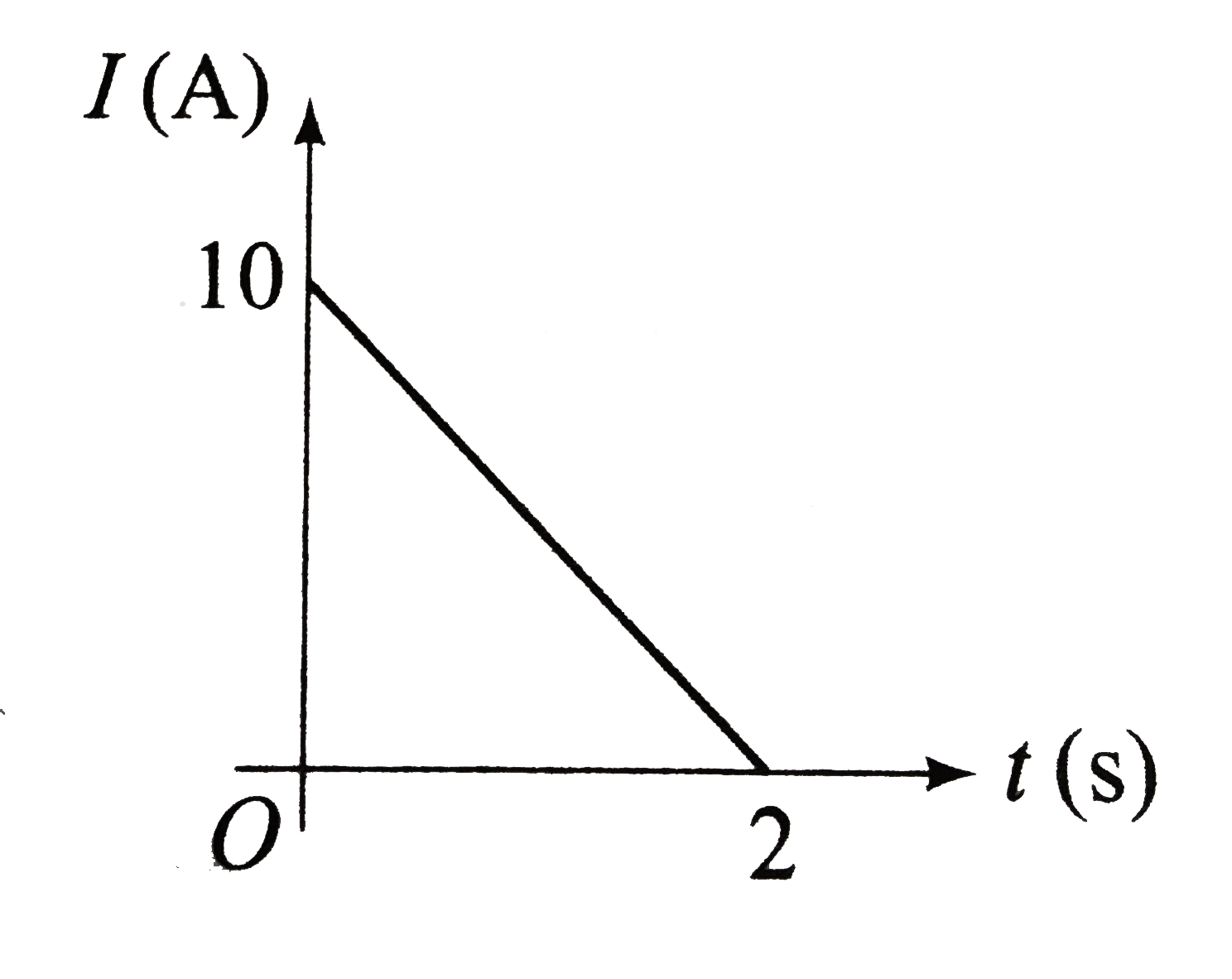 View Solution
View Solution

