Assertion: In an AC circuit, potential difference across the capacitor may be greater than the applied voltage.
Reason : VC=IXC, wheereas V=IZ and XC can be greater than Z also.
If both Assertion and Reason are true and the Reason is correct explanation of the Assertion.
If both Assertion and Reason are true but Reason is not the correct explanation of Assertion
If Assertion is true, but the Reason is false.
If Assertion is false but the Reason is true.
The correct Answer is:A
To solve the question, we need to analyze the assertion and reason provided regarding an AC circuit involving a capacitor.
1. Understanding the Assertion: The assertion states that in an AC circuit, the potential difference across the capacitor (Vc) may be greater than the applied voltage (V). This suggests that the voltage across the capacitor can exceed the total voltage supplied in the circuit.
2. Understanding the Reason: The reason given is that VC=IXC and V=IZ, where XC is the capacitive reactance and Z is the impedance of the circuit. It is stated that XC can be greater than Z.
3. Analyzing the Relationships:
- The voltage across the capacitor is given by VC=IXC.
- The total voltage in the circuit is given by V=IZ.
- The impedance Z can be expressed in terms of resistance R and reactance X (which includes both inductive and capacitive reactance).
4. Using the Pythagorean Theorem: In an AC circuit, the relationship between the voltages can be expressed as:
V=√V2R+(VL−VC)2
where VR is the voltage across the resistor, VL is the voltage across the inductor, and VC is the voltage across the capacitor.
5. Example Calculation: Let's consider an example where:
- VR=50V
- VL=100V
- VC=100V
Plugging these values into the equation:
V=√502+(100−100)2=√2500=50V
Here, VC (100 V) is greater than the applied voltage V (50 V).
6. Conclusion on Assertion: Since we have shown that VC can indeed be greater than V, the assertion is true.
7. Conclusion on Reason: The reason states that XC can be greater than Z. If XC is indeed greater than Z, it implies that the voltage across the capacitor can be significantly high, supporting the assertion.
8. Final Statement: Both the assertion and the reason are true, and the reason correctly explains the assertion.
Final Answer
Both the assertion and reason are true, and the reason is the correct explanation of the assertion.
---
- The voltage across the capacitor is given by VC=IXC.
- The total voltage in the circuit is given by V=IZ.
- The impedance Z can be expressed in terms of resistance R and reactance X (which includes both inductive and capacitive reactance).
V=√V2R+(VL−VC)2
where VR is the voltage across the resistor, VL is the voltage across the inductor, and VC is the voltage across the capacitor.
- VR=50V
- VL=100V
- VC=100V
V=√502+(100−100)2=√2500=50V
Here, VC (100 V) is greater than the applied voltage V (50 V).
Both the assertion and reason are true, and the reason is the correct explanation of the assertion.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Level - 1 Objective30videos
ALTERNATING CURRENT
- BOOK - DC PANDEY ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Level - 1 Subjective6videos
ALTERNATING CURRENT
- BOOK - DC PANDEY ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Exercise 28.22videos
ALTERNATING CURRENT
- BOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY42videos
ATOMS
Similar Questions
Can the potential difference across a battery be greater than its emf?
View SolutionCan the peak voltage across the inductor be greater than the peak voltage of the source in an LCR circuit?
View SolutionAssertion: In series, L-C-R voltage across capacitor is always less than the applied voltage.
Reason: In series L-C-R circuit, V=√(V2R+(V2L−V2C))View SolutionIn a series LCR circuit with an AC source, R=300Ω,C=20μF,L=1.0henry,εrms=50V and v=50πHz. Find (a) the rms current in the circuit and (b) the rms potential differences across the capacitor, the resistor and the inductor. Note that the sum of the rms potential differences across the three elements is greater than the rms voltage of the source.
View SolutionIn a series LCR circuit with an AC source, R=300Ω,C=20μF,L=1.0henry,εrms=50V and v=50πHz. Find (a) the rms current in the circuit and (b) the rms potential differences across the capacitor, the resistor and the inductor. Note that the sum of the rms potential differences across the three elements is greater than the rms voltage of the source.
View SolutionAssertion : Potential difference across the terminals of a battery is always less than the emf of the battery.
Reason : During discharging of a battery potential differnce across to terminals of a battery is
V=E−ir
∴V<EView SolutionThe given graph shows variation of charge .q. versus potential difference .V. for two capacitors

C1andC2. Both the capacitors have same plate separation but plate area of C2 is greater than that of C1. Which line (A or B) corresponds to C1 and why?View SolutionAssertion : In series L−C−R circuit, voltage will lead the current function for frequency greater than the resonance frequency.
Reason : At resonance frequency, phase difference between current function and voltage function is zero.View SolutionThe potential differences across the resistance, capacitance and inductance are 80V,40V and 100V respectively in an L−C−R circuit. The power factor of this circuit is
View SolutionTwo capacitors of capacitances 2C and C are connected in series with an inductor of inductance L. Initially, capacitors have charge such that VB−VA=4V0 and VC−VD=V0. Initial current in the circuit is zero. Find
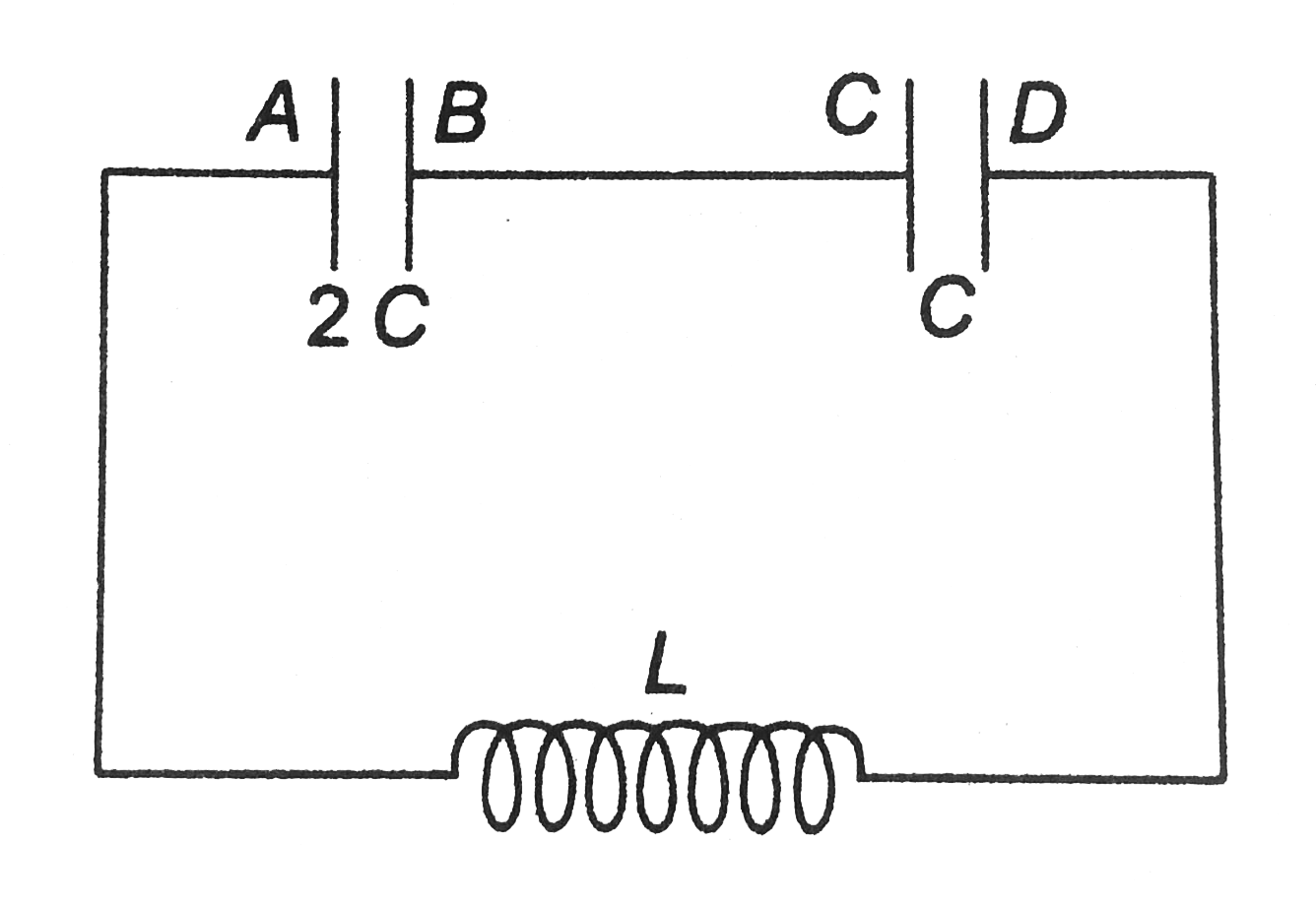
(a) maximum current that will flow in the circuit,
(b) potential difference across each capacitor at that instant,
(c) equation of current flowing towards left in the inductor.View Solution

