A 8 μ F capacitor is charged by a 400 V supply through 0.1 M Ω resistance. The time taken by the capacitor to develop a potential difference of 300V is : (Given log104=0.602)
2.2 sec
1.1 sec
0.55 sec
0.48 sec
The correct Answer is:D
To solve the problem, we need to determine the time taken by an 8 µF capacitor to develop a potential difference of 300 V when charged by a 400 V supply through a 0.1 MΩ resistor. We can use the formula for the charging of a capacitor in an RC circuit.
1. Identify the given values:
- Capacitance, C=8μF=8×10−6F
- Supply voltage, V=400V
- Resistance, R=0.1MΩ=0.1×106Ω=100,000Ω
- Desired voltage across the capacitor, Vc=300V
2. Use the formula for the voltage across a charging capacitor:
The voltage across a charging capacitor at time t is given by:
Vc=V(1−e−tRC)
Where:
- V is the supply voltage,
- R is the resistance,
- C is the capacitance,
- e is the base of the natural logarithm.
3. Rearranging the formula to solve for time t:
We can rearrange the formula to find t:
1−VcV=e−tRC
Taking the natural logarithm on both sides:
ln(1−VcV)=−tRC
Therefore:
t=−RC⋅ln(1−VcV)
4. Calculate 1−VcV:
1−300400=1−0.75=0.25
5. Substituting values into the equation:
Now we can substitute R, C, and ln(0.25) into the equation. First, we need to find ln(0.25):
ln(0.25)=ln(14)=−ln(4)
Given log10(4)=0.602, we can convert this to natural logarithm:
ln(4)=0.602×2.303≈1.386
Therefore:
ln(0.25)=−1.386
6. Calculate t:
Now substituting the values:
t=−RC⋅(−1.386)=RC⋅1.386
t=(100,000Ω)(8×10−6F)⋅1.386
t=0.8⋅1.386≈1.109s
7. Final Result:
Therefore, the time taken by the capacitor to develop a potential difference of 300 V is approximately:
t≈1.1s
- Capacitance, C=8μF=8×10−6F
- Supply voltage, V=400V
- Resistance, R=0.1MΩ=0.1×106Ω=100,000Ω
- Desired voltage across the capacitor, Vc=300V
The voltage across a charging capacitor at time t is given by:
Vc=V(1−e−tRC)
Where:
- V is the supply voltage,
- R is the resistance,
- C is the capacitance,
- e is the base of the natural logarithm.
We can rearrange the formula to find t:
1−VcV=e−tRC
Taking the natural logarithm on both sides:
ln(1−VcV)=−tRC
Therefore:
t=−RC⋅ln(1−VcV)
1−300400=1−0.75=0.25
Now we can substitute R, C, and ln(0.25) into the equation. First, we need to find ln(0.25):
ln(0.25)=ln(14)=−ln(4)
Given log10(4)=0.602, we can convert this to natural logarithm:
ln(4)=0.602×2.303≈1.386
Therefore:
ln(0.25)=−1.386
Now substituting the values:
t=−RC⋅(−1.386)=RC⋅1.386
t=(100,000Ω)(8×10−6F)⋅1.386
t=0.8⋅1.386≈1.109s
Therefore, the time taken by the capacitor to develop a potential difference of 300 V is approximately:
t≈1.1s
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-III29videos
ELECTROMAGNETIC INDUCTION
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE - I (MAGNETIC FLUX, FARADAY.S LAW, LENZ.S LAW, AC GENERATOR)26videos
ELECTROMAGNETIC INDUCTION
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-IB18videos
ELECTROMAGNETIC INDUCTION
- BOOK - AAKASH SERIESCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - PROBLEMS (LEVEL-II)26videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - EXERCISE -II22videos
ELECTROMAGNETIC WAVES
Similar Questions
A 4μF capacitor is charged to 400 volts and then its plates are joined through a resistor of resistance 1KΩ. The heat produced in the resistor is
View SolutionA 4μF capacitor is charged to 400 volts and then its plates are joined through a resistor of resistance 1KΩ. The heat produced in the resistor is
View SolutionThe 500μF capacitor is charged at a steady rate of 100μC/s. The potential difference across the capacitor will be 10 V after an interval of
View SolutionThe 500μF capacitor is charged at a steady rate of 100μC/s. The potential difference across the capacitor will be 10 V after an interval of
View SolutionA parallel combination of 0.1MΩ resistor and a 10μF capacitor is connected across a 1.5V source of negligible resistance. The time required for the capacitor to get charged up to 0.75 V is approximately (in seconds).
View SolutionAn 8(μ)F capacitor is connected across a 220√2 V, 50 Hz line. What is the peak value of charge through the capacitor?
View Solutiongiven that potential differene across 1μF capacitor is 10V. Then,
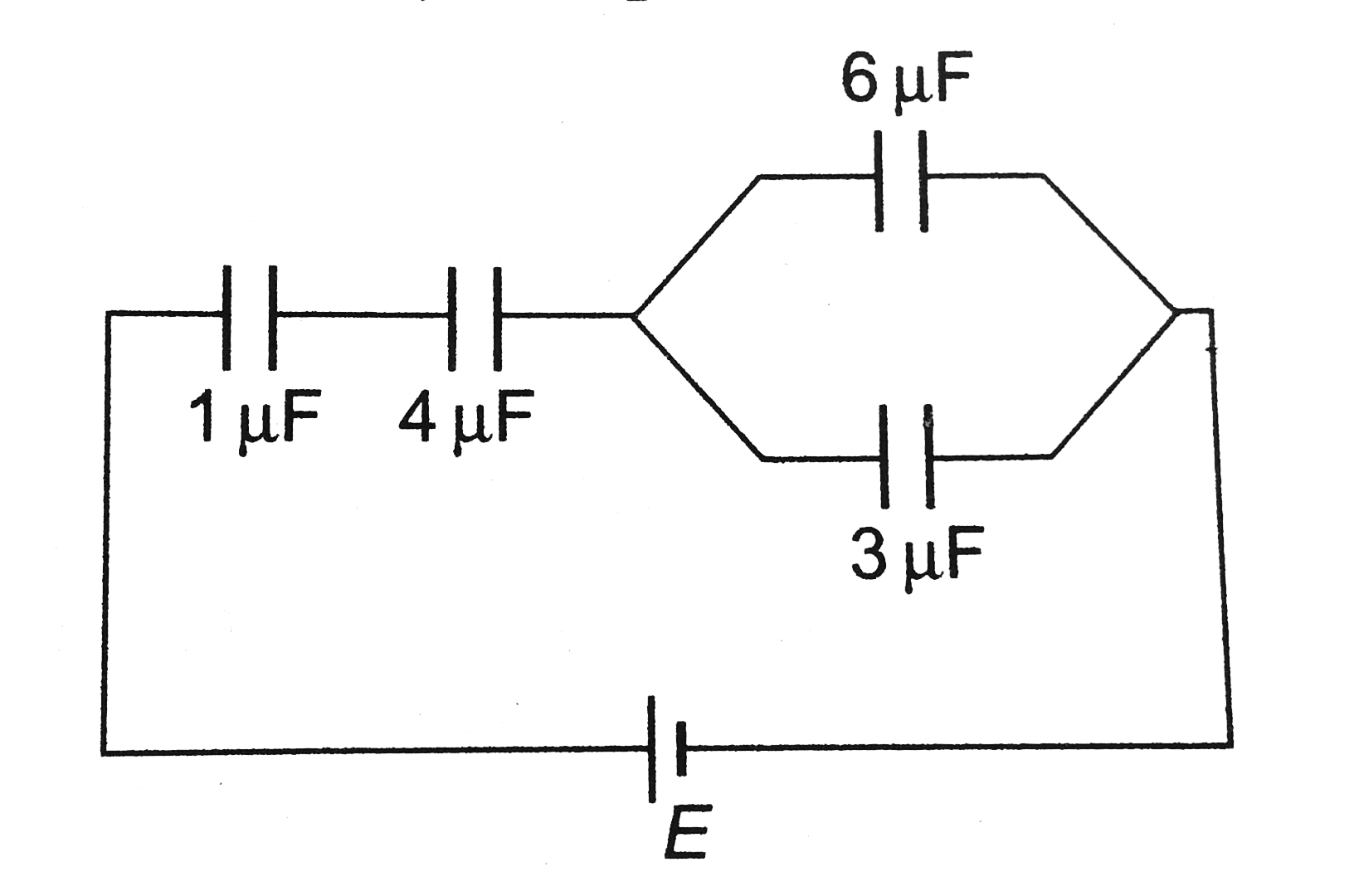 View Solution
View SolutionA 20(μ)Fcapacitor is joined to a battery of emf 6.0V through a resistance of 100(Ω).find the charge on the capacitor 2.0ms after the connections are made .
View SolutionA 100μF capacitor is charged to a potential difference of 24V. It is connected to an uncharged capacitor of capacitance 20μF What will be the new potential difference across the 100μF capacitor?
View SolutionA parallel combination of 0.1 MΩ resistor and a 10μF capacitor is connected across a 1.5 V source of negligible resistance. The time (in sec) required for the capacitor to get charged upto 0.75 V is approximately
View Solution

