A ball is projected from ground with a velocity V at an angle θ to the vertical. On its path it makes an elastic collison with a vertical wall and returns to ground. The total time of flight of the ball is
2vsinθg
2vcosθg
vsin2θg
vcosθg
To solve the problem of finding the total time of flight of a ball projected from the ground with a velocity V at an angle θ to the vertical, we can follow these steps:
Step 1: Understand the Components of the Velocity
The initial velocity V can be broken down into two components:
- The vertical component Vy=Vcos(θ)
- The horizontal component Vx=Vsin(θ)
Step 2: Calculate the Time of Flight Without Collision
In the absence of any collisions, the time of flight T for a projectile launched vertically can be calculated using the formula:
T=2Vyg
where g is the acceleration due to gravity.
Step 3: Substitute the Vertical Component
Substituting the vertical component into the time of flight formula, we have:
T=2(Vcos(θ))g
Step 4: Consider the Elastic Collision
Since the collision with the vertical wall is elastic, it does not affect the time of flight. The ball will bounce back with the same vertical velocity and will follow a symmetrical path. Therefore, the time of flight remains the same.
Step 5: Final Expression for Total Time of Flight
Thus, the total time of flight of the ball after the collision remains:
T=2Vcos(θ)g
Conclusion
The total time of flight of the ball is given by:
T=2Vcos(θ)g
The initial velocity V can be broken down into two components:
- The vertical component Vy=Vcos(θ)
- The horizontal component Vx=Vsin(θ)
In the absence of any collisions, the time of flight T for a projectile launched vertically can be calculated using the formula:
T=2Vyg
where g is the acceleration due to gravity.
Substituting the vertical component into the time of flight formula, we have:
T=2(Vcos(θ))g
Since the collision with the vertical wall is elastic, it does not affect the time of flight. The ball will bounce back with the same vertical velocity and will follow a symmetrical path. Therefore, the time of flight remains the same.
Thus, the total time of flight of the ball after the collision remains:
T=2Vcos(θ)g
The total time of flight of the ball is given by:
T=2Vcos(θ)g
Topper's Solved these Questions
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Only one option is correct for JEE Advanced
60 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - More a than one option is Correct
1 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery
27 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
Similar Questions
A particle is projected from the ground with velocity u making an angle θ with the horizontal. At half of its maximum heights,
View SolutionA ball of mass m is projected from the ground with an initial velocity u making an angle of θ with the vertical. What is the change in velocity between the point of projection and the highest point ?
View SolutionA particle of mass m is projected form ground with velocity u making angle θ with the vertical. The de Broglie wavelength of the particle at the highest point is
View SolutionA ball is projected from ground with a speed 70m/s at an angle 45∘ with the vertical so that it strikes a vertical wall at horizontal distance 4903m from the point of projection. If the ball returns back to the poin tof projection without any collision with ground then find the coefficient of restitution between the ball and wall.
View SolutionSTATEMENT-1: A body is projected from the ground with a velocity v at an angle with the horizontal direction, it reaches a maximum height (H) and reaches the ground after a time T = 2u sin θ/g
STATEMENT-2: The vertical and horizontal motions can be treated independently
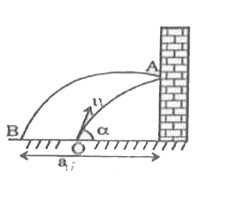
View SolutionA ball is projected from the ground with speed u at an angle α with horizontal. It collides with a wall at some distance from the point of projection and returns on the same level. Coefficient of restitution between the ball and the wall is e, then time taken in path AB and maximum height attained by the ball is
View SolutionA particle is projected vertically upwards from ground with velocity 10 m/s. Find the time taken by it to reach at the highest point ?
View SolutionA ball is projected from the ground with speed u at an angle α with horizontal. It collides with a wall at a distance a from the point of projection and returns to its original position. Find the coefficient of restitution between the ball and the wall.
View SolutionA body is projected vertically up with a velocity v and after some time it returns to the point from which it was projected. The average velocity and average speed of the body for the total time of flight are
View SolutionA body is projected vertically up with a velocity v and after some time it returns to the point from which it was projected. The average velocity and average speed of the body for the total time of flight are
View Solution
