Two identiacal masses are as shown in figure. One is thrown upwards with velocity 20 m/s and another is just dropped simultaneously.
In the above problem, to what maximum height (from ground) with the combined mass rise ?
25 m
18 m
15 m
20 m
To solve the problem of finding the maximum height to which the combined mass rises when one mass is thrown upwards with a velocity of 20 m/s and another mass is dropped simultaneously, we can follow these steps:
1. Identify the Initial Conditions:
- Let mass 1 (m1) be thrown upwards with an initial velocity u1=20m/s.
- Let mass 2 (m2) be dropped from rest, so its initial velocity u2=0m/s.
- The distance between the two masses is 20m.
2. Apply the Second Equation of Motion for Mass 1:
- For mass 1 (thrown upwards), we can use the equation:
s1=u1t−12gt2
- Here, g=10m/s2 (acceleration due to gravity).
- Thus, substituting the values:
s1=20t−12⋅10⋅t2=20t−5t2
3. Apply the Second Equation of Motion for Mass 2:
- For mass 2 (dropped), we can use the equation:
s2=u2t+12gt2
- Since u2=0:
s2=0+12⋅10⋅t2=5t2
4. Set Up the Equation for Total Distance:
- The total distance traveled by both masses must equal the initial distance between them:
s1+s2=20
- Substituting the expressions for s1 and s2:
(20t−5t2)+5t2=20
- Simplifying gives:
20t=20
- Thus:
t=1s
5. Calculate Distances Traveled by Each Mass:
- For mass 1:
s1=20(1)−5(1)2=20−5=15m
- For mass 2:
s2=5(1)2=5m
6. Determine the Maximum Height of the Combined Mass:
- After 1 second, mass 1 has risen 15 m, and mass 2 has fallen 5 m.
- The maximum height from the ground where the combined mass will rise is:
Height=15m (from mass 1)+5m (from mass 2)=15m
Final Answer:
The maximum height to which the combined mass rises is 15 meters.
- Let mass 1 (m1) be thrown upwards with an initial velocity u1=20m/s.
- Let mass 2 (m2) be dropped from rest, so its initial velocity u2=0m/s.
- The distance between the two masses is 20m.
- For mass 1 (thrown upwards), we can use the equation:
s1=u1t−12gt2
- Here, g=10m/s2 (acceleration due to gravity).
- Thus, substituting the values:
s1=20t−12⋅10⋅t2=20t−5t2
- For mass 2 (dropped), we can use the equation:
s2=u2t+12gt2
- Since u2=0:
s2=0+12⋅10⋅t2=5t2
- The total distance traveled by both masses must equal the initial distance between them:
s1+s2=20
- Substituting the expressions for s1 and s2:
(20t−5t2)+5t2=20
- Simplifying gives:
20t=20
- Thus:
t=1s
- For mass 1:
s1=20(1)−5(1)2=20−5=15m
- For mass 2:
s2=5(1)2=5m
- After 1 second, mass 1 has risen 15 m, and mass 2 has fallen 5 m.
- The maximum height from the ground where the combined mass will rise is:
Height=15m (from mass 1)+5m (from mass 2)=15m
The maximum height to which the combined mass rises is 15 meters.
Topper's Solved these Questions
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - More a than one option is Correct
1 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery
27 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
Similar Questions
Two identiacal masses are as shown in figure. One is thrown upwards with velocity 20 m/s and another is just dropped simultaneously.
The masses collide I air and stick together. After how much time the combined mass will fall to the gorund (calculate the time from the starting when the motion was started )
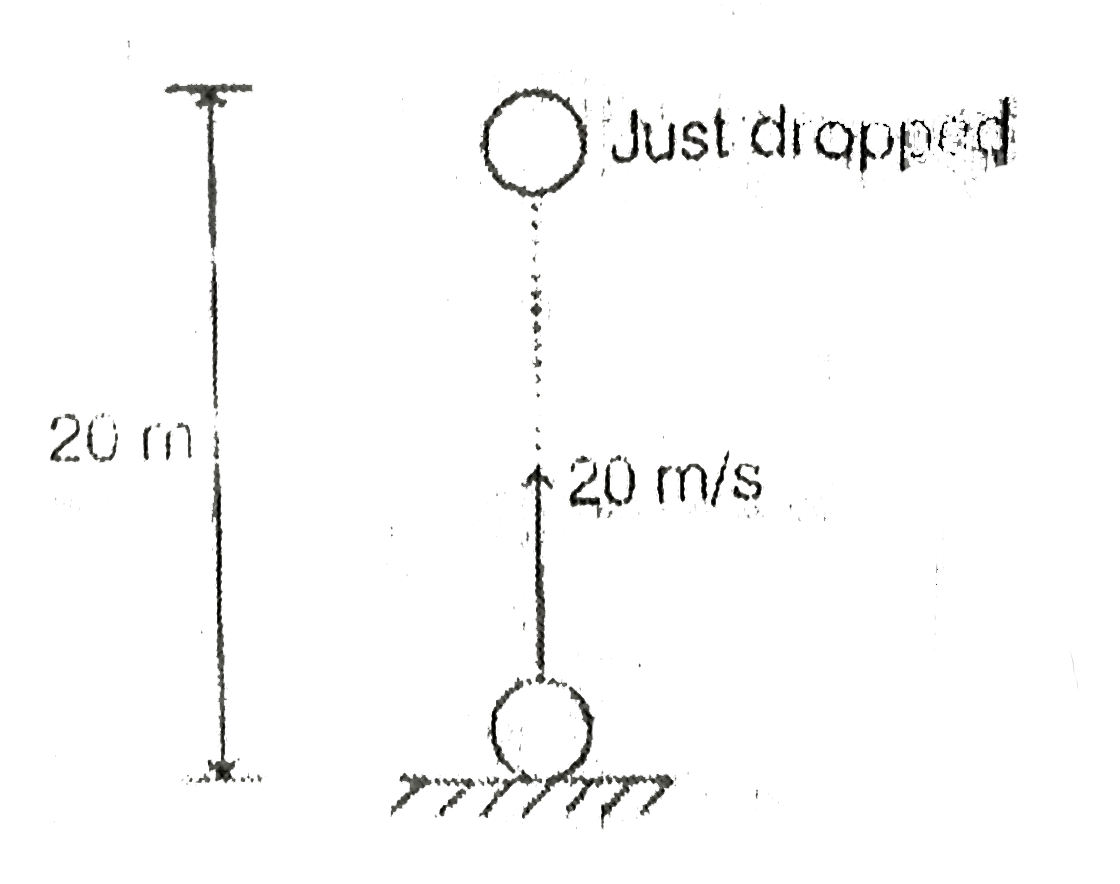
View SolutionTwo identical masses are as shown in figure. One is thrown upwards with velocity 20 m/s and another is just dropped simultaneously.
If the collision between them is elastic, find the time interval between their striking with ground
View SolutionA ball is thrown vertically upward with a velocity of 20 m/s. Calculate the maximum height attain by the ball.
View SolutionA body A is thrown up vertically from the ground with velocity V0 and another body B is simultaneously dropped from a height H. They meet at a height H2 if V0 is equal to
View SolutionTwo balls AandB of same masses are thrown from the top of the building A. Thrown upward with velocity VandB, thrown downward with velocity V, then
View SolutionA particle is thrown vertically upwards. If its velocity is half of the maximum height is 20m/s, then maximum height attained by it is
View SolutionA particle of mass 1 kg is projected upwards with velocity 60 m/s. Another particle of mass 2 kg is just deopper from a certain height. After 2 kg is just of the particles have colliided with ground, match the following [ Take g= 10 m/s2]
View SolutionAn object is thrown vertically upward with a speed of 30 m/s. The velocity of the object half-a-second before it reaches the maximum height is
View SolutionA body is thrown horizontally with a velocity of v m/s from the top of a tower of height 2h reaches the ground in 't' seconds. If another body double the mass is thrown horizontally with a velocity 5v m/s from the top of another tower of height 8h. In the above problem if the first reaches the ground at a horizontal distance 'x' the second body reaches the ground at a horizontal distance
View SolutionA ball is dropped from the top of a tower of height 78.4 m Another ball is thrown down with a certain velocity 2 sec later. If both the balls reach the ground simultaneously, the velocity of the second ball is
View Solution
