A ball is projected in a direction inclined to the vertical and bounces on a smooth horizontal plane. The range of one rebound is R. If the coefficient of restitution is e, then range of the next rebound is
R'=eR
R'=e2R
R'=Re
R'=R
The correct Answer is:A
To solve the problem, we need to determine the range of the next rebound of a ball that has already bounced once, given the initial range R and the coefficient of restitution e.
1. Understanding the Initial Conditions:
- A ball is projected at an angle θ to the horizontal.
- The range of the first rebound is given as R.
- The coefficient of restitution e affects the vertical component of the velocity after the bounce.
2. Range Formula:
- The range R of a projectile is given by the formula:
R=2u2sinθcosθg
- Here, u is the initial velocity, g is the acceleration due to gravity, and θ is the angle of projection.
3. Components of Velocity:
- The horizontal component of the initial velocity is:
ux=ucosθ
- The vertical component of the initial velocity is:
uy=usinθ
4. After the First Bounce:
- Upon bouncing, the horizontal component of the velocity remains unchanged:
u′x=ucosθ
- The vertical component of the velocity after the bounce is reduced by the coefficient of restitution:
u′y=e⋅(usinθ)
5. Calculating the Range of the Next Rebound:
- The range R′ for the next rebound can be calculated using the new vertical component:
R′=2(u′x)2sinθcosθg
- Substituting u′x and u′y:
R′=2(ucosθ)2(e⋅(usinθ))cosθg
- This simplifies to:
R′=2(u2cos2θ)(e⋅(usinθ))g
- Rearranging gives:
R′=e⋅R
6. Final Result:
- Therefore, the range of the next rebound is:
R′=eR
Summary:
The range of the next rebound is directly proportional to the range of the first rebound multiplied by the coefficient of restitution e.
- A ball is projected at an angle θ to the horizontal.
- The range of the first rebound is given as R.
- The coefficient of restitution e affects the vertical component of the velocity after the bounce.
- The range R of a projectile is given by the formula:
R=2u2sinθcosθg
- Here, u is the initial velocity, g is the acceleration due to gravity, and θ is the angle of projection.
- The horizontal component of the initial velocity is:
ux=ucosθ
- The vertical component of the initial velocity is:
uy=usinθ
- Upon bouncing, the horizontal component of the velocity remains unchanged:
u′x=ucosθ
- The vertical component of the velocity after the bounce is reduced by the coefficient of restitution:
u′y=e⋅(usinθ)
- The range R′ for the next rebound can be calculated using the new vertical component:
R′=2(u′x)2sinθcosθg
- Substituting u′x and u′y:
R′=2(ucosθ)2(e⋅(usinθ))cosθg
- This simplifies to:
R′=2(u2cos2θ)(e⋅(usinθ))g
- Rearranging gives:
R′=e⋅R
- Therefore, the range of the next rebound is:
R′=eR
The range of the next rebound is directly proportional to the range of the first rebound multiplied by the coefficient of restitution e.
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Multiple Correct
25 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning
2 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Subjective
23 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
A partical falls from a height h upon a fixed horizontal plane and rebounds. If e is the coefficient of restitution, the total distance travelled before rebounding has stopped is
View SolutionA ball of mass M falls from a height h on a floor which the coefficient of restitution is e. The height attained by the ball after two rebounds is
View Solution
Knowledge Check
A ball is dropped from a height h on to a floor . If the cofficient of restitution is e, calculate the height the ball first rebounds ?
Ae2hBeh2Ce4hDhe4
A steel ball strikes a fixed smooth steel plate placed on a horizontal surface atan angle θ with the vertical. If the coefficient of restitution is e, the angle at which the rebound will take place is:
View SolutionA steel ball strikes a fixed smooth steel plate placed on a horizontal surface at an angle θ with the vertical. If the coefficient of restitution is e, the angle at which the rebound will take place is:
View SolutionA ball is dropped on the ground from a height of 1m. The coefficient of restitution is 0.6. The height to which the ball will rebound is
View SolutionA ball is dropped on the ground from a height 10 m. If coefficient of restitution f 0.4, then find the height of which ball will rebound.
View SolutionA glass ball collides with a smooth horizontal surface (xz plane) with a velocity V=ai−bj. If the coefficient of restitution of collision be e, the velocity of the ball just after the collision will be
View SolutionA ball is dropped on a smooth inclined plane and is observed to move horizontally after the impact. The coefficient of restitution between the plane and ball is e. The inclination of the plane is
View SolutionA wedge of mass M and angle α rests on a smooth horizontal plane. A smooth sphere of mass m strickes it in a direction perpendicular to its inclined face and rebounds. If the coefficient of restitution is e, find the ratio of the speed of the sphere just before and just after the impact.
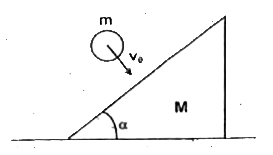
View Solution
