A ball is released in a smooth dimetrical tunnel of earth
a. After how much time will it pass through the center of earth?
b. With what speeed will the ball pass the center earth?
To solve the problem of a ball released in a smooth diametrical tunnel through the Earth, we will break it down into two parts:
Part a: Time to Pass Through the Center of the Earth
1. Understanding the Forces: When the ball is released, it experiences gravitational force towards the center of the Earth. The gravitational force inside the Earth varies linearly with distance from the center.
2. Acceleration Inside the Earth: The acceleration a of the ball at a distance r from the center of the Earth is given by:
a=−GMr2
However, since we are considering the ball inside the Earth, the effective mass M that contributes to the gravitational force is only the mass enclosed within radius r. This can be expressed as:
a=−gR3r
where g is the acceleration due to gravity at the surface and R is the radius of the Earth.
3. Simple Harmonic Motion: The motion of the ball can be modeled as simple harmonic motion (SHM) with angular frequency ω:
ω=√gR
4. Time Period of SHM: The time period T of the SHM is given by:
T=2π√Rg
Since the ball will take half the period to reach the center, the time t to pass through the center is:
t=T2=π√Rg
Part b: Speed at the Center of the Earth
1. Conservation of Energy: The potential energy lost by the ball as it falls towards the center is converted into kinetic energy. The potential energy at the surface is:
PE=−GMmR
and at the center, it is:
PEcenter=0
The change in potential energy is:
ΔPE=0−(−GMmR)=GMmR
2. Kinetic Energy at the Center: The kinetic energy at the center when the ball reaches there is given by:
KE=12mv2
Setting the change in potential energy equal to the kinetic energy gives:
GMmR=12mv2
3. Solving for Speed: Canceling m from both sides and solving for v:
v2=2GMR
Using g=GMR2, we can express v as:
v=√2gR
Final Answers:
- a. The time to pass through the center of the Earth is t=π√Rg.
- b. The speed of the ball at the center of the Earth is v=√2gR.
a=−GMr2
However, since we are considering the ball inside the Earth, the effective mass M that contributes to the gravitational force is only the mass enclosed within radius r. This can be expressed as:
a=−gR3r
where g is the acceleration due to gravity at the surface and R is the radius of the Earth.
ω=√gR
T=2π√Rg
Since the ball will take half the period to reach the center, the time t to pass through the center is:
t=T2=π√Rg
PE=−GMmR
and at the center, it is:
PEcenter=0
The change in potential energy is:
ΔPE=0−(−GMmR)=GMmR
KE=12mv2
Setting the change in potential energy equal to the kinetic energy gives:
GMmR=12mv2
v2=2GMR
Using g=GMR2, we can express v as:
v=√2gR
- a. The time to pass through the center of the Earth is t=π√Rg.
- b. The speed of the ball at the center of the Earth is v=√2gR.
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective
21 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single Correct
107 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.1
23 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
Is it necessary for the plane of the orbit of a satellite to pass through the Centre of the earth?
View SolutionAssertion : Plane of a satellite always passes through the centre of earth
Reason : Gravitational force on satellite is always towards centre of earth.
View SolutionA body weighs 200N on the surface of the earth. How much will it weigh half way down to the center of the earth ?
View SolutionA ball of mass m is dropped from a height h in a tunnel, made across the earth (mass = M, radius = R) passing through its center. If h<<R such that the motion of the particle through h can be considered uniformly accelerated at g, then the time period of the particle is
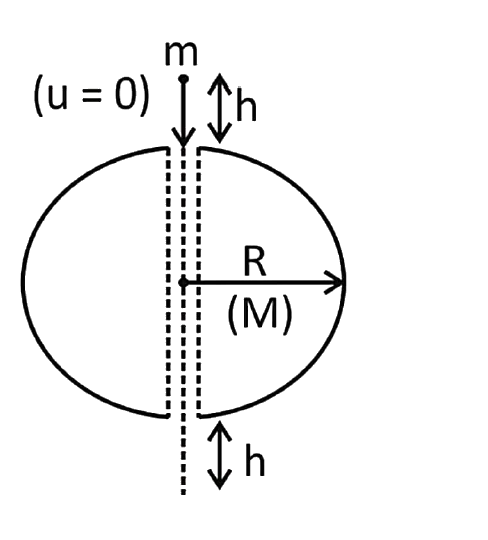
View SolutionWhat impulse need to be given to a body of mass m, released from the surface of earth along a straight tunnel passing through centre of earth, at the centre of earth, to bring it to rest. (Mass of earth M, radius of earth R)

View SolutionA diametrical tunnel is dug across the earth. A ball dropped into the tunnel from one side. The velocity of the ball when it reaches the centre of the earth is [Given: gravitational potential at the centre of earth =−3/2(GM/R)]
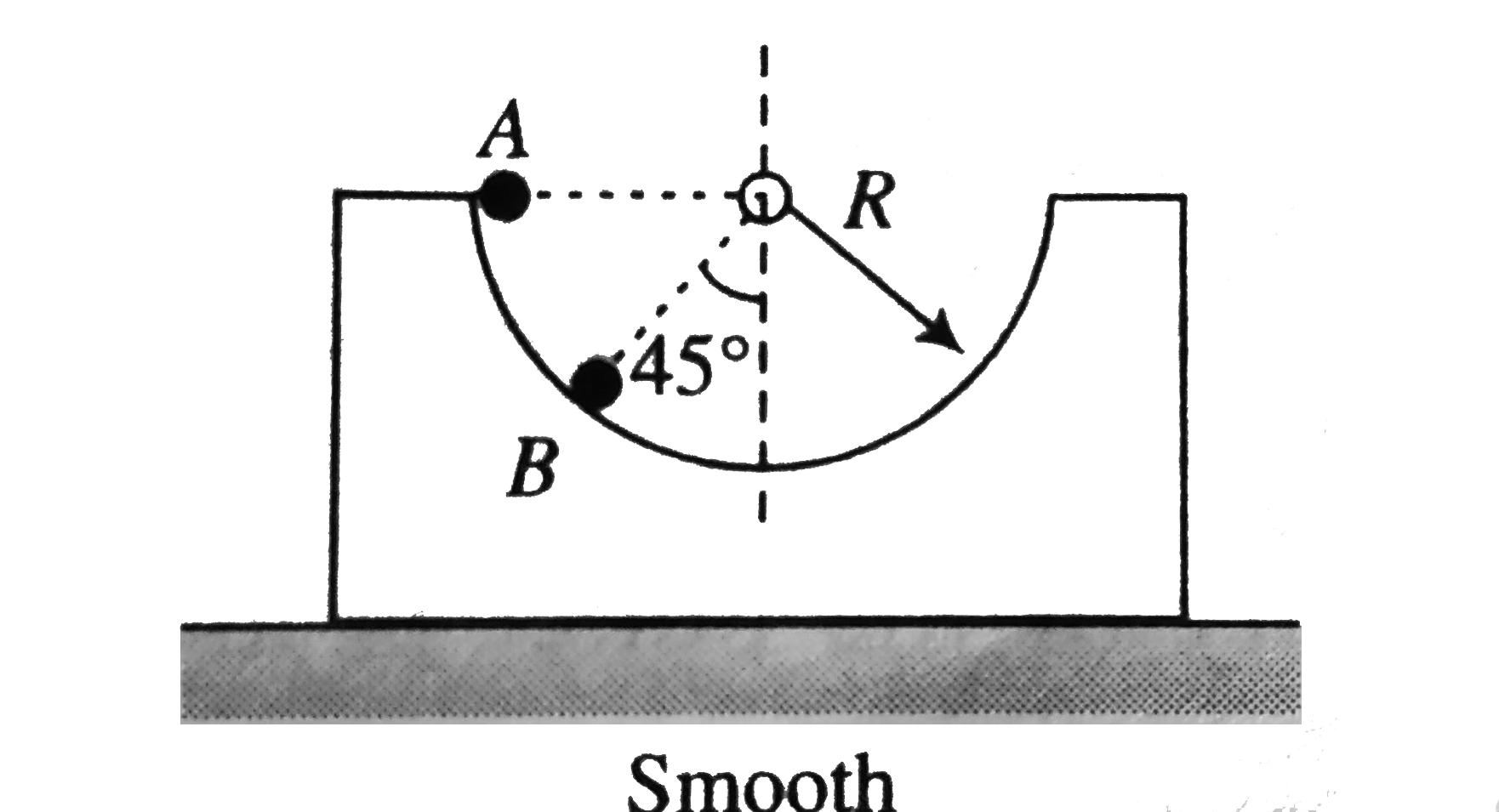
View SolutionA ball of mass m is released from A inside a smooth wedge of mass m as shown in figure. What is the speed of the wedge when the ball reaches point B?
View SolutionA ball is thrown upward with an ini tial velocity of 100ms−1. After how much time will it return ? Draw velocity - time graph for the ball and find from the graph (i) the maximum height attained by the ball and (ii) height of the ball after 15 s. Take g=10ms−2 .
View SolutionA train 140 m long us running at 60 km per hour . In how much time will it pass a tunnel 260 m long ?
View SolutionThe free surface of a liquid resting in an inertial frame is horizontal. Does the normal to the free surface pass through the centre of the earth? Think separately if the liquid is a. at te equaltor b. at a pole c. somewhere else.
View Solution
