A ball moving along a straight line collides elastically with another stationary ball of the same mass. At the moment of collision, the angle between the straight line passing through the centres of the balls and the direction of tr initial motion of the striking ball is $θ$ , find the fraction of the kinetic energy of the striking ball converted into potential energy at the moment of the maximum deformation.
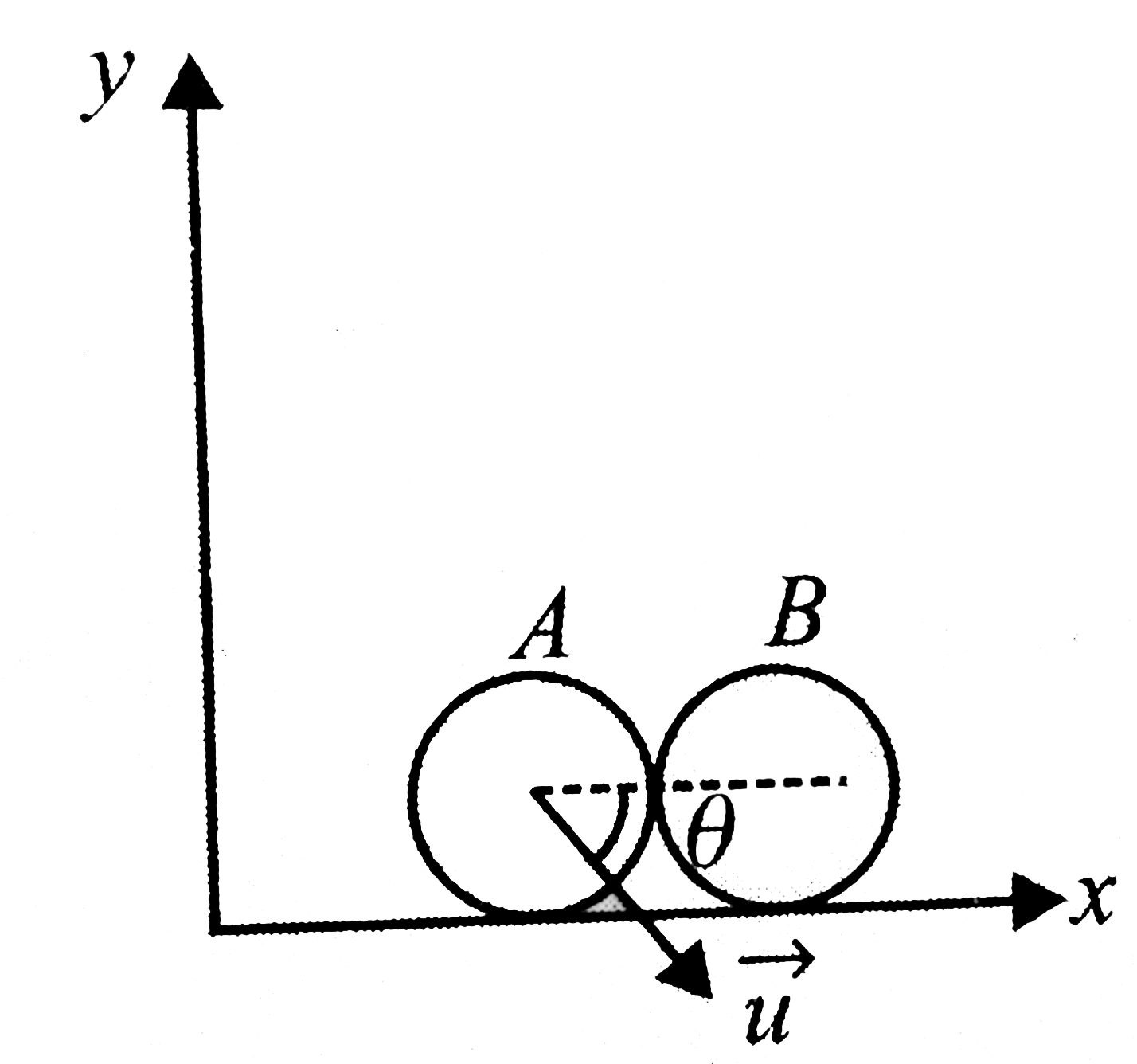
$A ball moving along a straight line collides elastically with another stationary ball of the same mass. At the moment of collision, the angle between the straight line passing through the centres of the balls and the direction of tr initial motion of the striking ball is theta, find the fraction of the kinetic energy of the striking ball converted into potential energy at the moment of the maximum deformation.$

Text Solution

Verified by Experts

Let a ball $A$ of mass $m$ moving with velocity $\vec{v}$ collide with stationary ball $B$ as shown in figure. As there is no external force, the linear momentum is conserved. As collision is two dimentional, the $x$ and $y$ components of the linear momentum are separately conserved.

Let ${\vec{v}}_{1}$ and ${\vec{v}}_{2}$ be the velocities of the particle after collision.
Then conservation of linear momentum along $x$ - axis gives
$mu \cos θ = m v_{1 x} + m v_{2 x}$
$\Rightarrow v_{1 x} + v_{2 x} = u \cos θ$ ..........i
and conservation of linear momentum along $y$ -axis gives
$mu \cos θ = m v_{1 x} + m v_{2 y}$
$\Rightarrow v_{1 y} + v_{2 y} = u \sin θ$ ............ii ltbr> at the moment of maximum deformation
$\Rightarrow v_{1 x y} = v_{2 x} = \frac{u \cos θ}{2}$ [using eqn i ]
and the tangential velocities iof balls before and after collision should be equal.
$u \sin θ = v_{1 y}$ and $v_{2 y} = 0$
Initial $K E E_{i} = \frac{1}{2} {mu}^{2}$
Final $K E$
$E_{f} = \frac{1}{2} m v_{1 x}^{2} + \frac{1}{2} m v_{1 y}^{2} + \frac{1}{2} m v_{2 x}^{2} + \frac{1}{2} m v_{2 y}^{2}$
$= \frac{1}{2} m (v_{1 x}^{2} + v_{2 x}^{2}) + \frac{1}{2} m v_{1 y}^{2} \frac{+}{2} m v_{2 y}^{2}$
$m v_{1 x}^{2} + \frac{1}{2} m v_{1 y}^{2} + 0$ (since $v_{1 x} = v_{2 x})$
$= m {(\frac{u \cos θ}{2})}^{2} + \frac{1}{2} m {(u \sin θ)}^{2}$
$= \frac{1}{4} {mu}^{2} \cos^{2} θ + \frac{1}{2} {mu}^{2} \sin^{2} θ$
$= \frac{1}{2} {mu}^{2} {\frac{1}{2} \cos^{2} θ + \sin^{2} θ}$
$= \frac{1}{2} {mu}^{2} {\cos^{2} θ + \sin^{2} θ - \frac{1}{2} \cos^{2} θ}$
$= \frac{1}{2} {mu}^{2} {1 - \frac{1}{2} \cos^{2} θ}$
Fraction of $K E$ converted into $P E$ at the moment of maximum deformation
$f = \frac{E_{i} - E_{f}}{E_{i}} = \frac{\frac{1}{2} μ^{2} - \frac{1}{2} {mu}^{2} (1 - \frac{\cos^{2} θ}{2})}{\frac{1}{2} μ^{2}} = \frac{\cos^{2} θ}{2}$
Here $θ = 45^{\circ}$ ,
$∴ f = \frac{\cos^{2} 45^{\circ}}{2} = \frac{1}{4} = 0.25$

Updated on:21/07/2023