A ball moving translationally collides elastically with another, stationary, ball of the same mass. At the moment of impact the angle between the straight line passing through the centres of the balls and the direction of the initial motion of the striking ball is equal to α=45∘. Assuming the balls to be smooth, find the fraction η of the kinetic energy of the striking ball that turned into potential energy at the moment of the maximum deformation.
If (v1x,v1y) are the instantaneous velocity components of the incident ball and (v2x,v2y) are the velocity components of the stuck ball at the same moment, then since there are no external impulsive forces (i.e. other than the mutual interaction of the balls)
We have usinα=v1y, v2y=0
mucosα=mv1x+mv2x
The impulsive force of mutual interaction satisfies
ddx(v1x)=Fm=−ddt(v2x)
(F is along the x axis as the balls are smooth. Thus Y component of momentum is not transferred). Since loss of K.E. is stored as deformation energy D, we have
D=12mu2−12mv21−12mv22
=12mu2cos2α−12mv21x−12mv22x
=12m[m2u2cos2α−m2v21x−(mucosα−mv1x)2]
=12m[2m2ucosαv1x−2m2v21x]=m(v1xucosα−v21x)
=m[u2cos2α4−(ucosα2−v1x)2]
We see that D is maximum when
ucosα2=v1x
and Dmax=mu2cos2α4
Then η=Dmax12mu2=12cos2α=14
On substituting α=45∘

Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Universal Gravitation34videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Dynamics Of A Solid Body56videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - The Fundamental Equation Of Dynamics59videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation36videos
OSCILLATIONS AND WAVES
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Transport Phenomena38videos
THERMODYNAMICS AND MOLECULAR PHYSICS
Similar Questions
A ball moving along a straight line collides elastically with another stationary ball of the same mass. At the moment of collision, the angle between the straight line passing through the centres of the balls and the direction of tr initial motion of the striking ball is θ, find the fraction of the kinetic energy of the striking ball converted into potential energy at the moment of the maximum deformation.
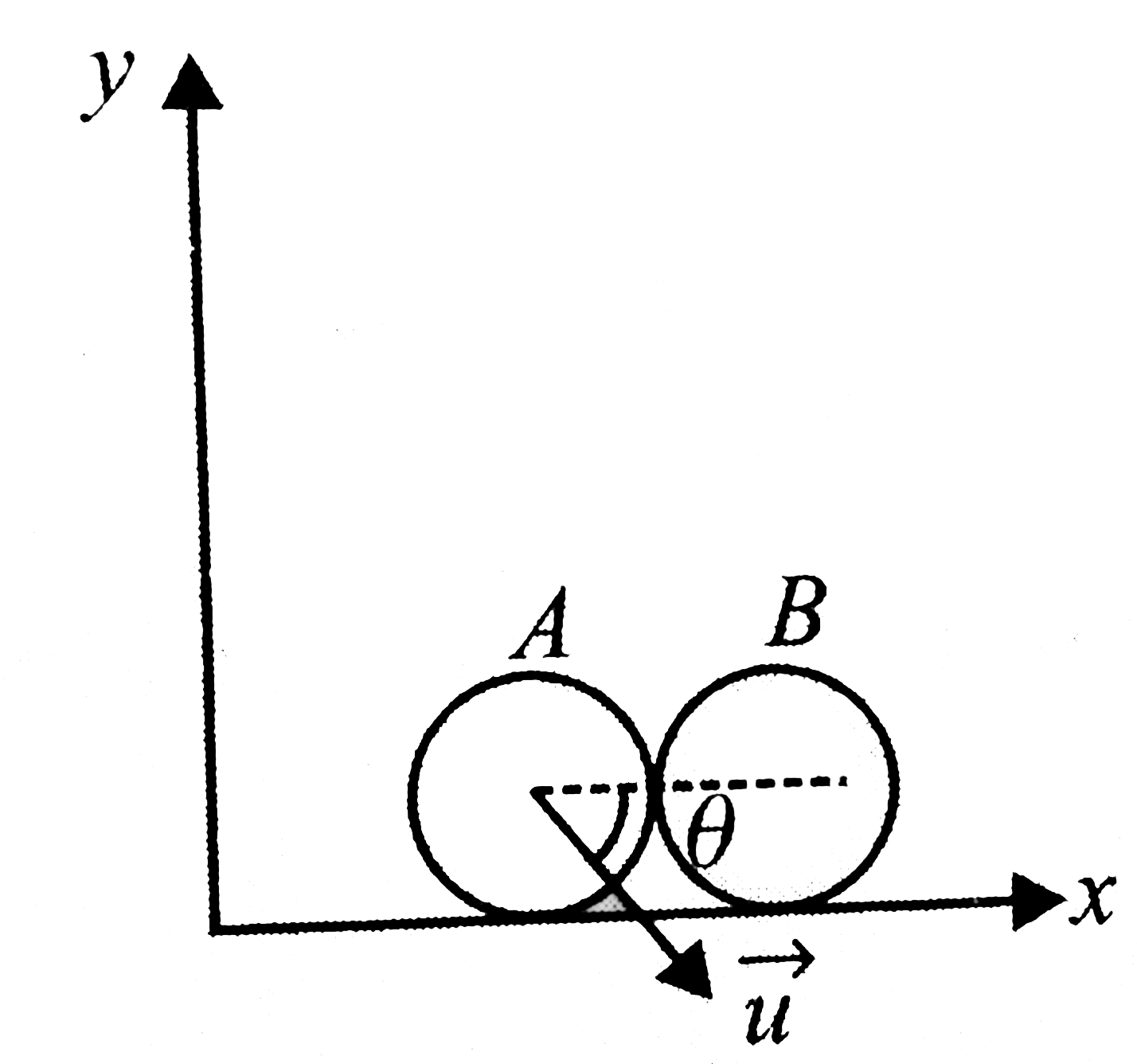 View Solution
View SolutionA ball of mass M collides elastically with another stationary ball of mass m. If M>m, find the maximum angle of deflection of M.
View Solution
Knowledge Check
- Question 1 - Select One
A ball of mass M moving with speed v collides perfectly inelastically with another ball of mass m at rest. The magnitude of impulse imparted to the first ball is
AMvBmvCMmM+mvDM2M+mv - Question 2 - Select One
A ball of mass 'm', moving with uniform speed, collides elastically with another stationary ball. The incident ball will lose maximum kinetic energy when the mass of the stationary ball is
AmB2mC4mDinfinity - Question 3 - Select One
A ball of mass 'm', moving with uniform speed, collides elastically with another stationary ball. The incident ball will lose maximum kinetic energy when the mass of the stationary ball is
AmB2 mC4 mDInfinity
Consider an oblique elastic collision between a moving ball and a stationary ball of the same mass. Both the balls move with the same speed after the collision. After the collision, the angle between the directions of motion of two balls is x degree. Find the value of x.
View SolutionA ball of mass m moving with velocity v collides head on elastically with another identical ball moving with velocity - V. After collision
View SolutionA ball of mass M moving with a velocity v collides perfectly inelastically with another ball of same mass but moving with a velocity v in the opposite direction. After collision
View SolutionA ball of mass m moving with a velocity v undergoes an oblique elastic collision with another ball of the same mass m but at rest. After the collision if the two balls move with the same speeds , the angle between their directions of motion will be:
View SolutionConsider the situation as shown in the diagram , the ball strikes the wall normally and the collision is elastic , the change in the kinetic energy of the ball is
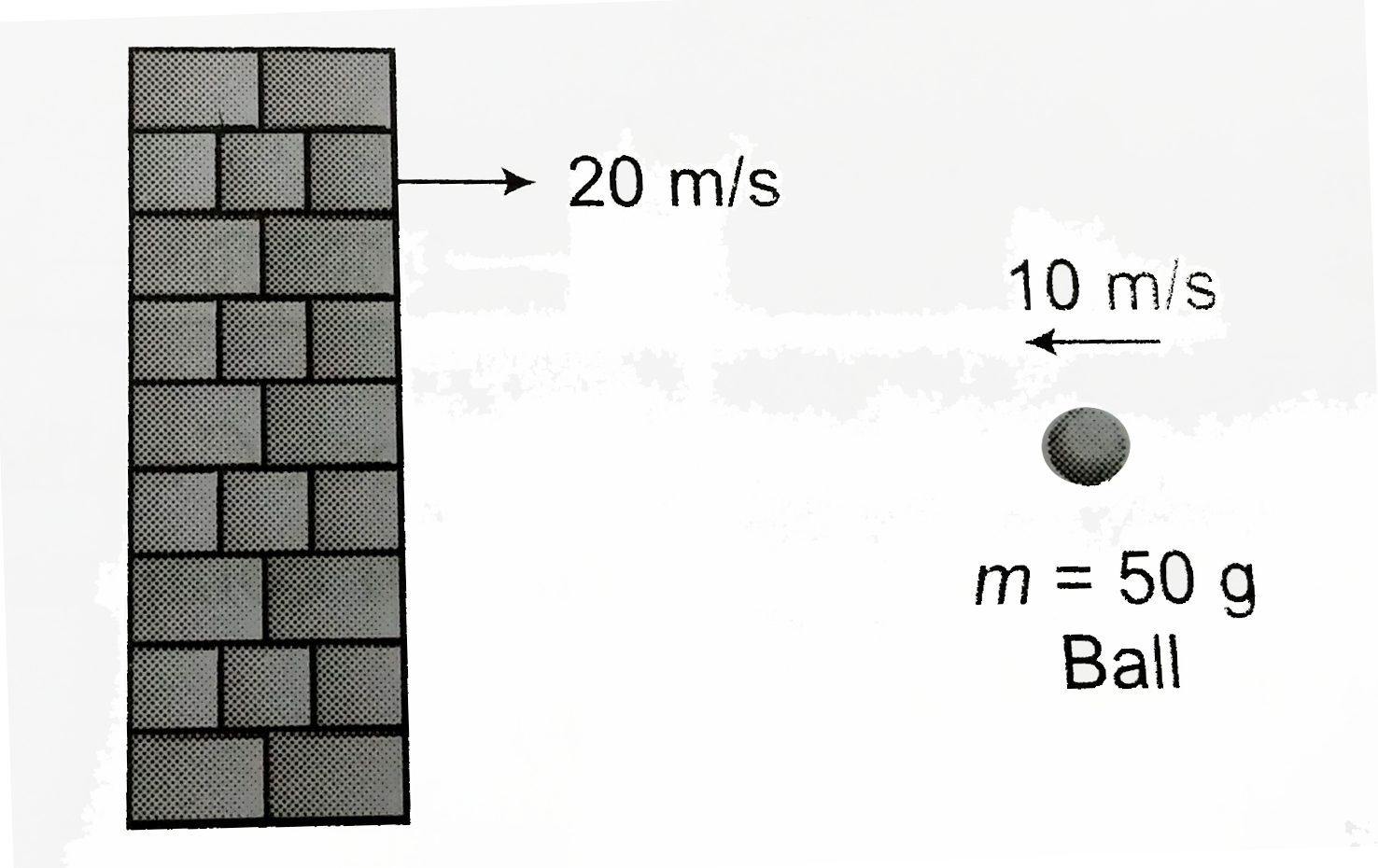 View Solution
View Solution

