A ball of 0.5 kg colided with wall at 30∘ and bounced back elastically.The speed of ball was 12m/s. The contact remained for 1s. What is the force applied by wall on ball?
12√3N
√3N
6√3N
3√3N
The correct Answer is:A
To solve the problem, we will follow these steps:
Step 1: Understand the scenario
The ball collides with the wall at an angle of 30∘ and bounces back elastically. The mass of the ball is 0.5kg and its speed before the collision is 12m/s. The contact time with the wall is 1s.
Step 2: Determine the initial and final momentum components
Since the collision is elastic, we need to analyze the momentum in the direction perpendicular to the wall (horizontal direction).
- The initial horizontal momentum (Pi) can be calculated using:
Pi=m⋅v⋅cos(θ)
where m=0.5kg, v=12m/s, and θ=30∘.
Step 3: Calculate the initial horizontal momentum
Using the cosine of 30∘:
cos(30∘)=√32
Now substituting the values:
Pi=0.5⋅12⋅√32=3√3kg m/s
Step 4: Determine the final momentum
After the collision, the ball bounces back elastically, meaning it retains the same speed but in the opposite direction. Therefore, the final horizontal momentum (Pf) is:
Pf=−m⋅v⋅cos(θ)=−3√3kg m/s
Step 5: Calculate the change in momentum
The change in momentum (ΔP) is given by:
ΔP=Pf−Pi=−3√3−3√3=−6√3kg m/s
Step 6: Calculate the force
Using the formula for force:
F=ΔPΔt
Substituting the values:
F=−6√31=−6√3N
The negative sign indicates that the force is in the opposite direction of the initial momentum (which is expected as the wall exerts a force in the opposite direction).
Final Answer
The magnitude of the force applied by the wall on the ball is:
F=6√3N
The ball collides with the wall at an angle of 30∘ and bounces back elastically. The mass of the ball is 0.5kg and its speed before the collision is 12m/s. The contact time with the wall is 1s.
Since the collision is elastic, we need to analyze the momentum in the direction perpendicular to the wall (horizontal direction).
Pi=m⋅v⋅cos(θ)
where m=0.5kg, v=12m/s, and θ=30∘.
Using the cosine of 30∘:
cos(30∘)=√32
Now substituting the values:
Pi=0.5⋅12⋅√32=3√3kg m/s
After the collision, the ball bounces back elastically, meaning it retains the same speed but in the opposite direction. Therefore, the final horizontal momentum (Pf) is:
Pf=−m⋅v⋅cos(θ)=−3√3kg m/s
The change in momentum (ΔP) is given by:
ΔP=Pf−Pi=−3√3−3√3=−6√3kg m/s
Using the formula for force:
F=ΔPΔt
Substituting the values:
F=−6√31=−6√3N
The negative sign indicates that the force is in the opposite direction of the initial momentum (which is expected as the wall exerts a force in the opposite direction).
The magnitude of the force applied by the wall on the ball is:
F=6√3N
Topper's Solved these Questions
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(AIIMS)
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Integer type questions
14 Videos
- SOUND WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SOUND WAVESEXERCISE - Exercise 19.7
4 Videos
Similar Questions
A ball hits a vertical wall horizontal at 10 m/s bounces back at 10 m/s
View SolutionA 3-kg steel ball strikes a wall with a speed of 10.0ms−1 at an angle of 60.0∘ with the surfaces of the wall. The ball bounces off with the same speed and same angle. If the ball was in contact with the wall for 0.2s, find the average force exerted by the wall on the ball.
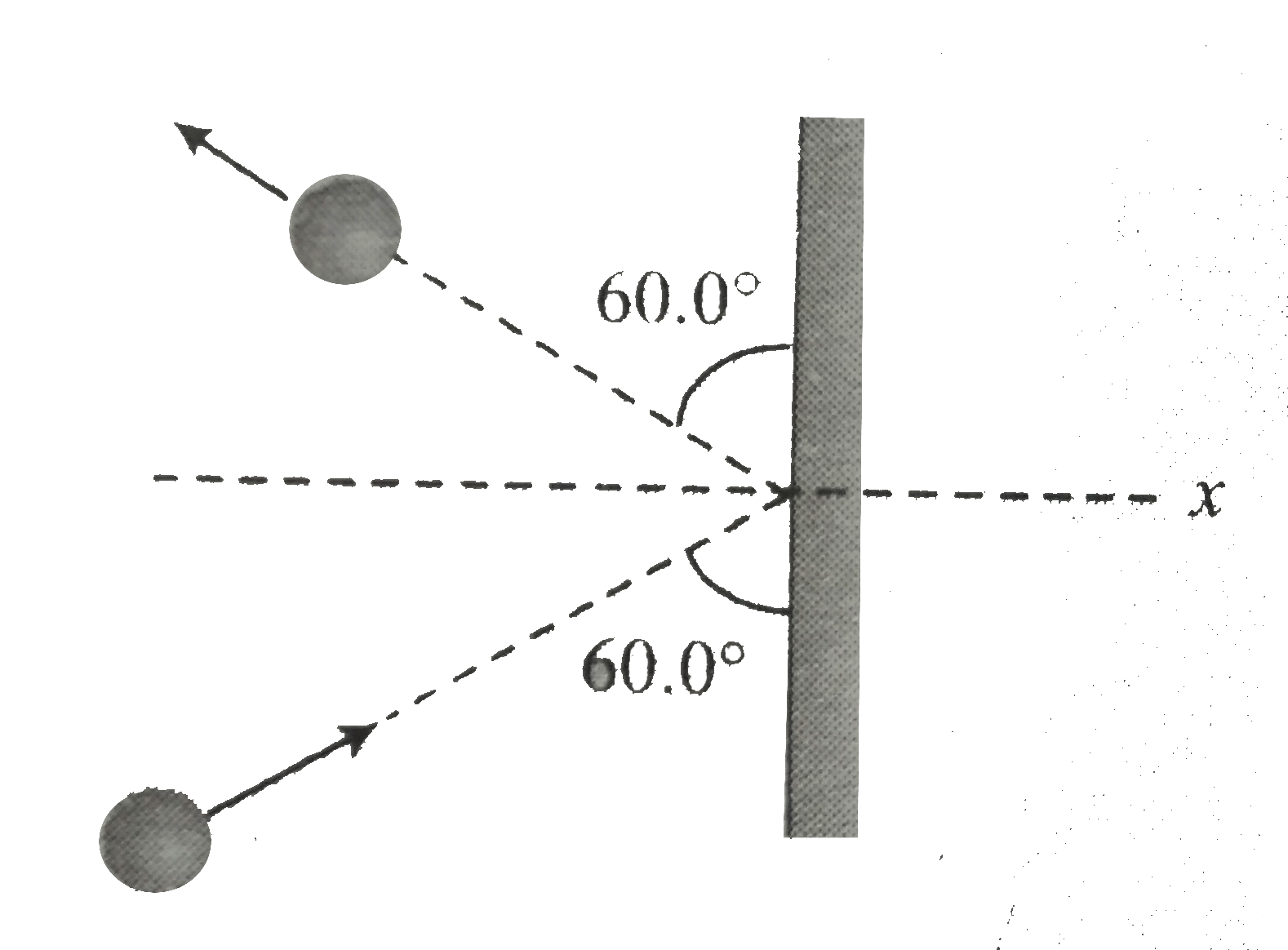
View Solution
Knowledge Check
A ball of mass m collides with a wall with speed v and rebounds on the same line with the same speed. If the mass of the wall is taken as infinite, then the work done by the ball on the wall is
Amv2B12mv2C2mvDzeroA ball of mass 0.5 kg, initially at rest, acquires a speed of 4 m/s immediately after being kicked by a force of strength 20 N. for how long did this force act on the ball?
A0.01sB0.02sC0.1sD0.2s
A rubber ball of mass 0.4 kg hits the ground at same angle without any change in speed . If the speed of ball is 1 m/s and the period of contact between the ball and floor is 0.4 s, find the average force exerted by the ball on the ground .
View SolutionA ball of mass 0.5kg moving with a velocity of 2m/s strikes a wall normally and bounces back with the same speed . If the time of contact between the ball and the wall is 1 millisecond , the average force exerted by the wall on the ball is
View SolutionA ball of mass 0.5kg moving with a velocity of 2m/s strikes a wall normally and bounces back with the same speed . If the time of contact between the ball and the wall is 1 millisecond , the average force exerted by the wall on the ball is
View SolutionA 3.00kg steel hall strikes the wall with a speed of 10.0m/s at an angle of 60∘ with the surface. It bounces off with the same speed and angle. If the ball is in contact with the wall for 0.200s, what is the average force exerted by the wall on the ball?
View SolutionA ball of mass 3kg moving with a speed of 100 m/s, strikes a wall at an angle 60∘ (as shown in figure). The ball rebounds at the same speed and remains in contact with the wall for 0.2 s, the force exerted by the ball on the wall is

View SolutionA 150 g ball, moving horizontally at 20m/s was hit straight back to bowler at 12m/s. If contact with bat lasted for 0.04 sec, then average force exerted by the bat on the ball is:-
View Solution
