A ball of mass 1.00 kg is attached to a loose string fixed to a ceiling. The ball is released from rest and falls 2.00 m, where the string suddenly stops it. Find the impulse on it from the string.
The correct Answer is:6.26 N.s
To solve the problem of finding the impulse on a ball of mass 1.00 kg that falls 2.00 m before being stopped by a string, we can follow these steps:
Step 1: Understand the situation
The ball is released from rest and falls under the influence of gravity. When it falls 2.00 m, the string becomes taut and stops the ball.
Step 2: Determine the initial and final velocities
- Initial velocity (u): Since the ball is released from rest, u=0m/s.
- Final velocity (v): When the string stops the ball, the final velocity is v=0m/s at the moment of stopping.
Step 3: Calculate the velocity just before the string stops the ball
To find the velocity just before the string stops the ball, we can use the principle of conservation of energy. The potential energy lost by the ball is converted into kinetic energy.
1. Potential energy (PE) lost:
ΔPE=mgh
where:
- m=1.00kg (mass of the ball)
- g=10m/s2 (acceleration due to gravity)
- h=2.00m (height fallen)
Thus,
ΔPE=1.00×10×2.00=20J
2. Kinetic energy (KE) just before the string stops the ball:
KE=12mv2
Setting the change in potential energy equal to the kinetic energy:
20=12×1.00×v2
Solving for v2:
20=0.5×v2⟹v2=40⟹v=√40≈6.32m/s
Step 4: Calculate the impulse
Impulse (I) is defined as the change in momentum, which can also be expressed as:
I=mΔv
where Δv=v−u.
Since the ball comes to a stop, we have:
- u=√40m/s
- v=0m/s
Thus,
Δv=0−√40=−√40
Now substituting into the impulse formula:
I=mΔv=1.00×(−√40)=−√40kg m/s
The negative sign indicates that the impulse is in the opposite direction of the ball's initial motion.
Step 5: Calculate the numerical value of the impulse
I≈−6.32kg m/s
Final Answer
The impulse on the ball from the string is approximately 6.32kg m/s in the upward direction.
---
The ball is released from rest and falls under the influence of gravity. When it falls 2.00 m, the string becomes taut and stops the ball.
- Initial velocity (u): Since the ball is released from rest, u=0m/s.
- Final velocity (v): When the string stops the ball, the final velocity is v=0m/s at the moment of stopping.
To find the velocity just before the string stops the ball, we can use the principle of conservation of energy. The potential energy lost by the ball is converted into kinetic energy.
ΔPE=mgh
where:
- m=1.00kg (mass of the ball)
- g=10m/s2 (acceleration due to gravity)
- h=2.00m (height fallen)
ΔPE=1.00×10×2.00=20J
KE=12mv2
Setting the change in potential energy equal to the kinetic energy:
20=12×1.00×v2
Solving for v2:
20=0.5×v2⟹v2=40⟹v=√40≈6.32m/s
Impulse (I) is defined as the change in momentum, which can also be expressed as:
I=mΔv
where Δv=v−u.
- u=√40m/s
- v=0m/s
Δv=0−√40=−√40
Now substituting into the impulse formula:
I=mΔv=1.00×(−√40)=−√40kg m/s
I≈−6.32kg m/s
The impulse on the ball from the string is approximately 6.32kg m/s in the upward direction.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (Single Correct Choice )47videos
CENTER OF MASS
- BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (More than One Correct Choice)5videos
CENTER OF MASS
- BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (Integer )4videos
CENTER OF MASS
- BOOK - RESNICK AND HALLIDAYCHAPTER - CAPACITANCEEXERCISE - PRACTICE QUESTION (INTEGER TYPE)3videos
CAPACITANCE
- BOOK - RESNICK AND HALLIDAYCHAPTER - CIRCUITSEXERCISE - Practice Questions (Integer Type)3videos
CIRCUITS
Similar Questions
A ball of mass 1kg is attached to an inextensible string. The ball is released from the position shown in figure. Find the impulse imparted by the string to the ball immediately after the string becomes taut.
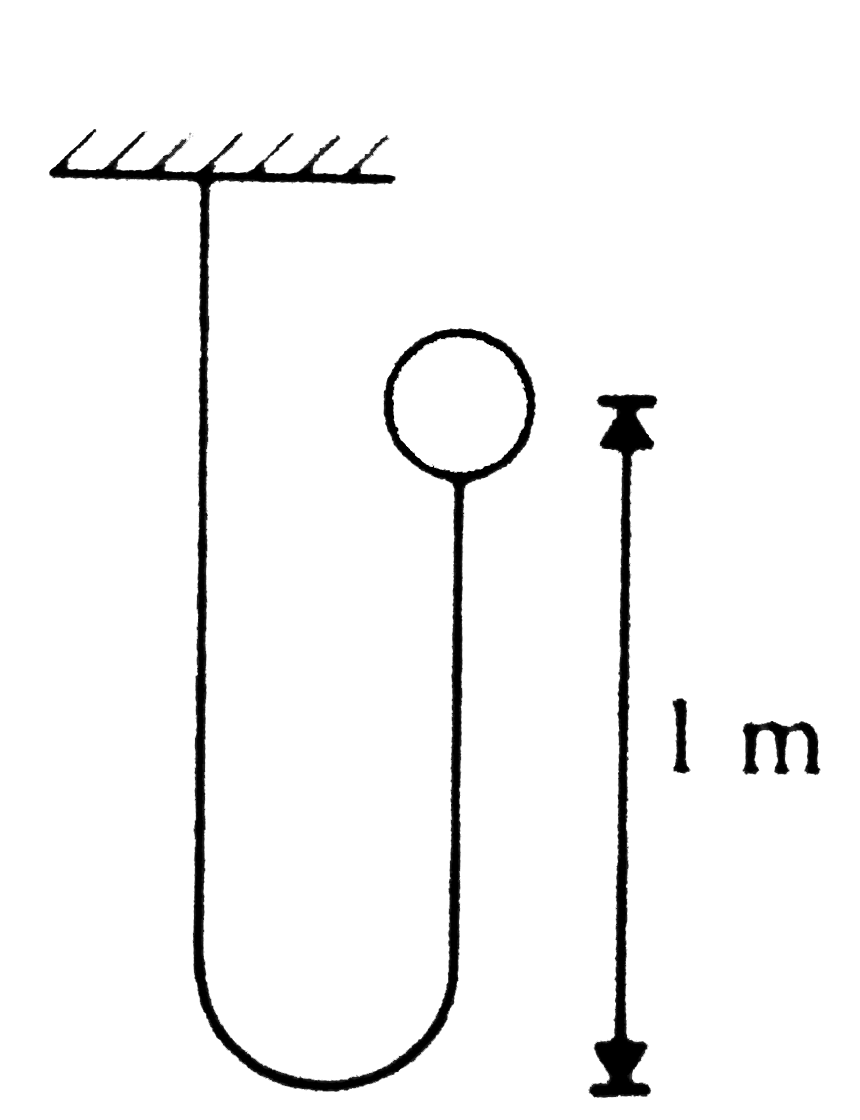 View Solution
View SolutionA ball of mass 1kg is attached to an inextensible string. The ball is released from the position shown in figure. Find the impulse imparted by the string to the ball immediately after the string becomes taut. (Take g=10m/s2)
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A ball of mass m is attached to a string whose other end is fixed. The system is free to rotate in vertical plane. When the ball swings, no work is done on the ball by the tension in the string. Which of the following statement is the correct explanation?
ATension is always perpendicular to the direction of motion of the ball.BTension is an internal force for the ball.CTension is an external force for the ball.DSince the ball is swinging about the axis, total displacement is zero. - Question 2 - Select One or More
A pendulum is made by attaching a ball at the end of a string (the other end of the string is attached to the ceiling). The ball is released from rest at the position shown at some angle ϕ. Which of the following vectors may represent the impulse delivered by the string to the ball from the time it is released unitl the ball is at the bottom of the swing when string becomes vertical
 A
A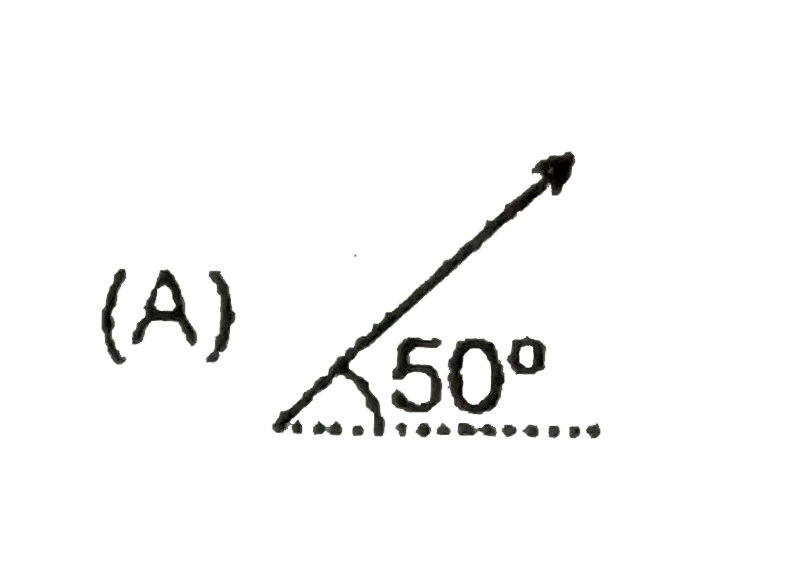 B
B C
C D
D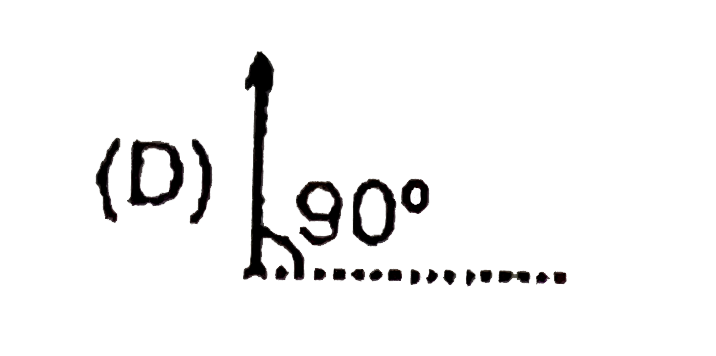
- Question 3 - Select One
Two massless string of length 5 m hang from the ceiling very near to each other as shown in the figure. Two balls A and B of masses 0.25kg and 0.5kg are attached to the string. The ball A is released from rest at a height 0.45m as shown in the figure. The collision between two balls is completely elastic. Immediately after the collision, the kinetic energy of ball B is 1J The velocity of ball A just after the collision is
Q01.png) A5 m s−1 to the rightB5 m s−1 to the leftC1 m s−1 to the rightD1 m s−1 to the left
A5 m s−1 to the rightB5 m s−1 to the leftC1 m s−1 to the rightD1 m s−1 to the left
A particle of mass 1kg is attached to a string of length 5m. The string is attached to a fixed point O. It is released from the position as shown in Fig. Calculate
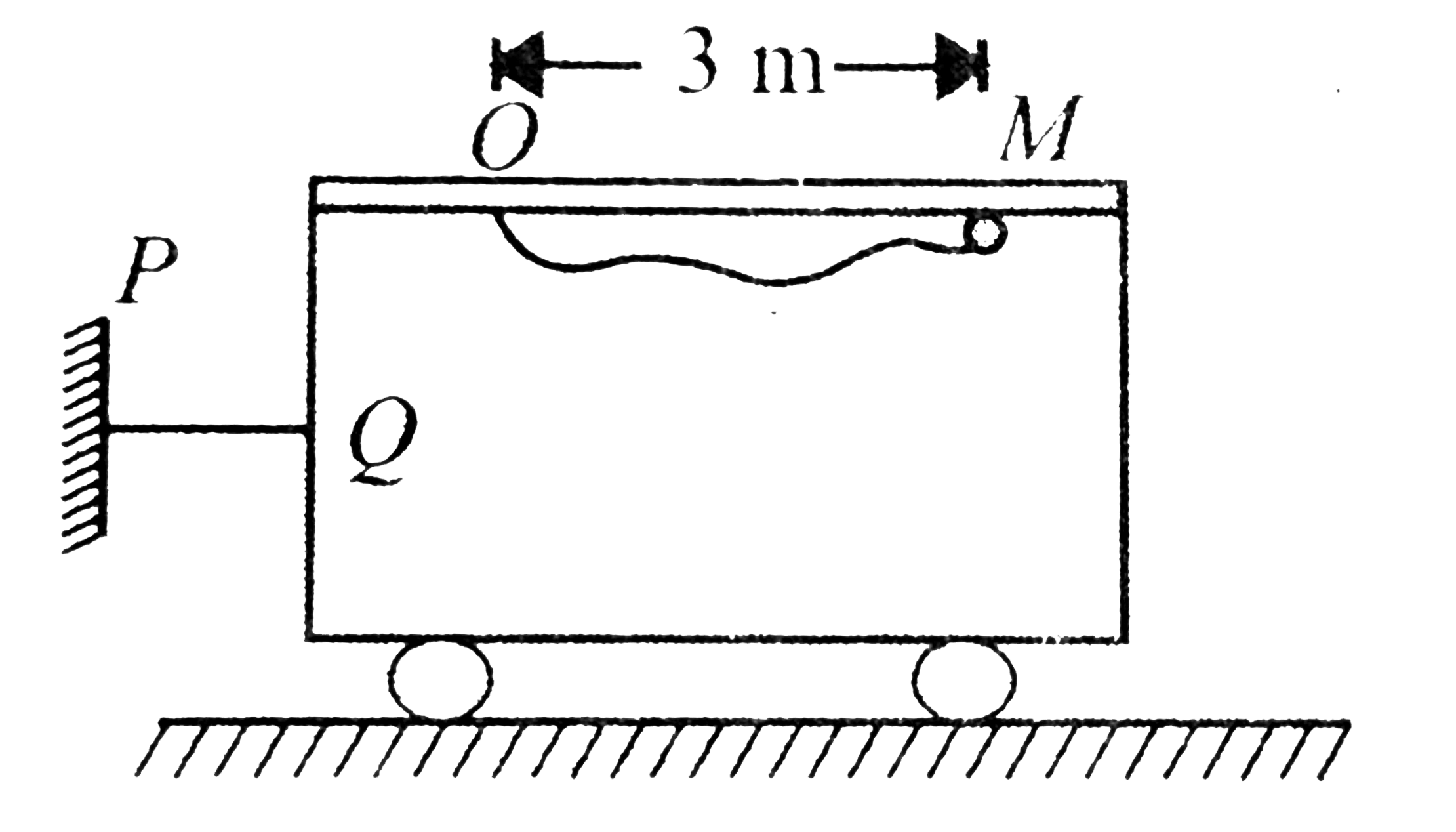
a. the impulse developed in the string when it becomes taut,
b. the velocity of the particle just after the string becomes taut,
c. the impulse developed in this string PQ at this instant.View SolutionA ball of mass 0.5 kg is attached to a light string of length 2m. The ball is whirled on la horizontal smooth surface is a circle of rdius 2 m as shown in fig. If the string can withstand tension up to 100 N, what is the maximum speed at which the bal can be whirled.
 View Solution
View SolutionA simple pendulum consists of a ball of mass m connected to a string of length L. The ball is pulled aside so that the string makes an angle of 53∘ with the verticle and is released. Find the ratio of the minumum and the tension in the string.
View SolutionTwo massless string of length 5 m hang from the ceiling very near to each other as shown in the figure. Two balls A and B of masses 0.25kg and 0.5kg are attached to the string. The ball A is released from rest at a height 0.45m as shown in the figure. The collision between two balls is completely elastic. Immediately after the collision, the kinetic energy of ball B is 1J The velocity of ball A just after the collision is
Q01.png) View Solution
View SolutionThe ring R in the arrangement shown can slide along a smooth fixed, horizontal rod XY. It is attached to the block B by a light string. The block is released from rest, with the string horizontal. Then which of the following are true.
 View Solution
View Solution

