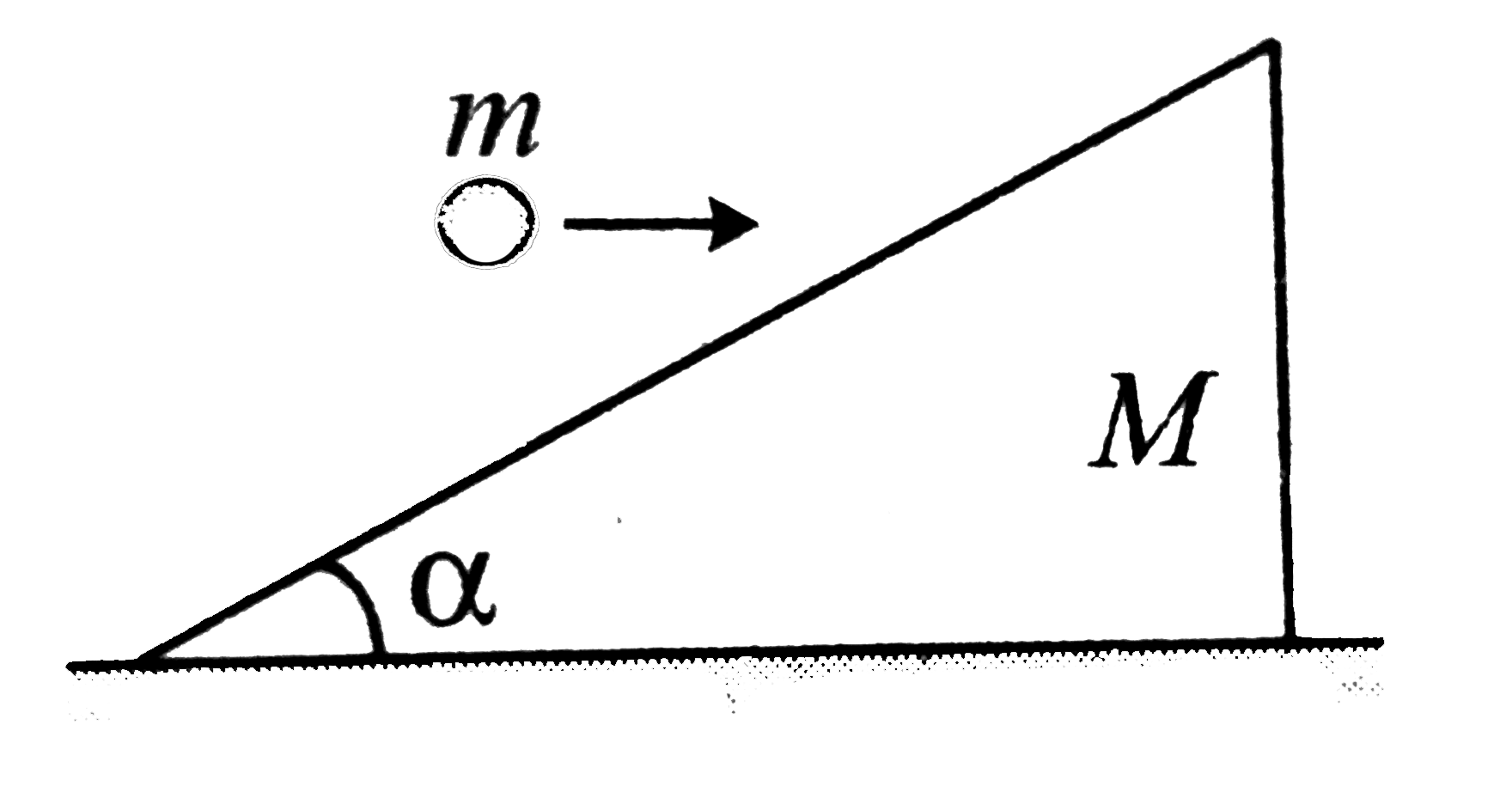
A ball of mass m moving with constant horizontal velocity u strikes a stationary wedge of mass M on its inclined surface as shown in the figure. After collision, the ball starts moving up the inclined plane. The wedge is placed on frictionless horizontal surface.
a. Calculate the velocity of wedge immediately after collision.
b. Calculate the maximum height the ball can ascend on the wedge.
The correct Answer is:musin2αM+msin2α)
a. Let after collision velocity of wedge be V and that of ball be v0 as shown v0 is w.r.t. wedge. Applying conservation of lienar momentum along x-axis, we get
μ=Mv+m(V+v0cosα)….i
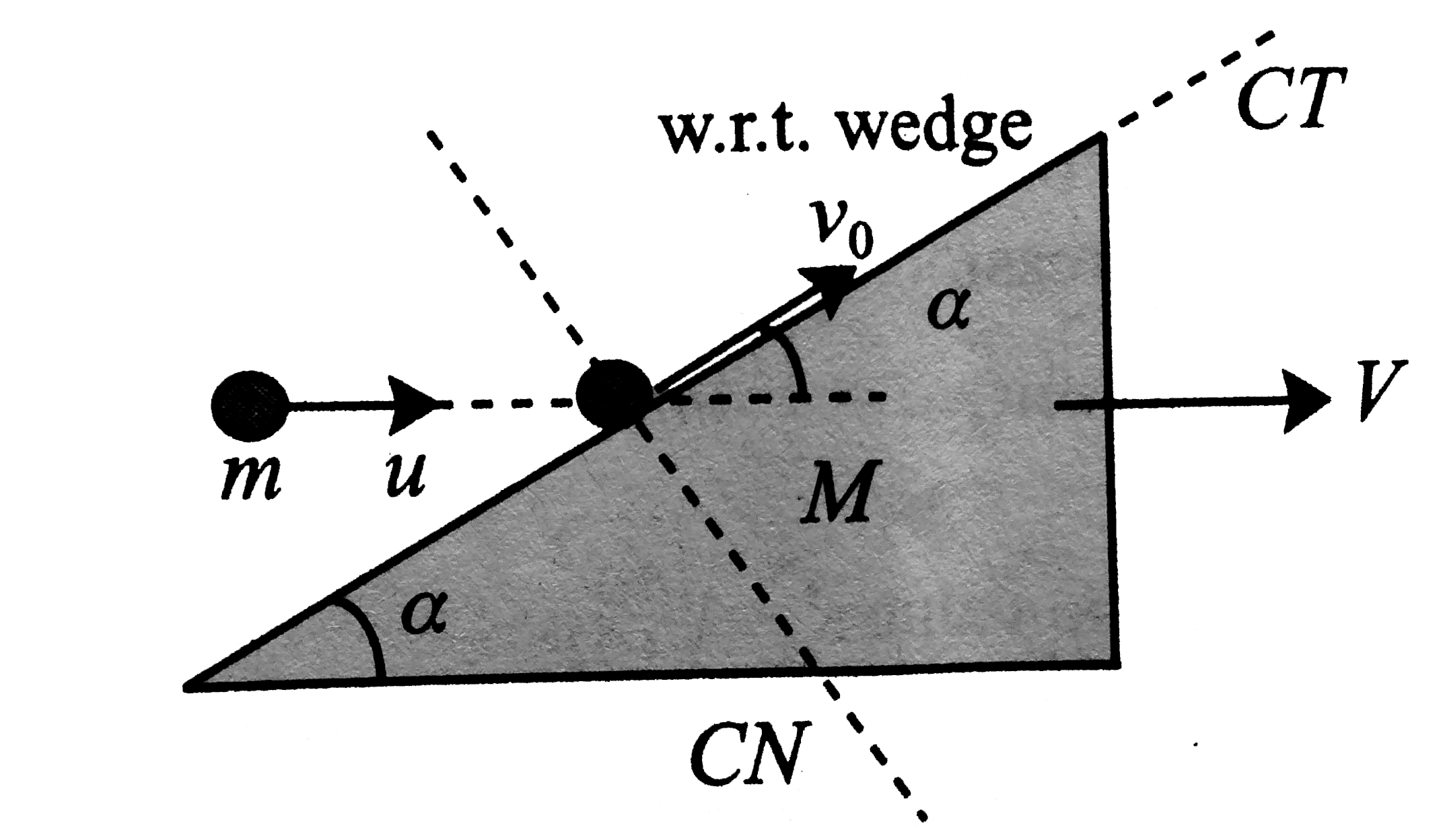
Velocity along CT remains, constant
ucosα=v0+Vcosα.......ii
→vb=(v0cosα+V)ˆi+(v0sinα)ˆj
From i and ii
mu=MV+mV+mcosα(ucosα−Vcosα)
=(M+m)V+μcos2α−mcos2α
⇒V=musin2αM+msin2α
b. When the bal ascends maximum height, then ball will be at rest w.r.t. wedge and ther velocity will be same. Let their common velocity be v'. From conservationof momentum we cn find this common velocity as 'v'=mu(M+m).
From ii v0−(u−V)cosα, put the value of V in this to get
v0=MucosαM+msin2α
Also, v0cosα+V=[Mcos2α+msin2αM+msin2α]u
To find maximum height
From energy conservation
mgh+12(m+M)v'2
=12MV2+12m(v0cosα+V)2+12m(v0sinα)2
2mgh+m2u2M+m=MV2+m(v0cosα+V)2+m(v0sinalpa)2
2mgh+m2u2M+m
Mm2u2sin4α+m(Mcos2α+msin2α)2u2
=+mM2u2cos2αsin2α(M+msin2α)2
Solve to get: h=u22g[M2cos2α(M+m)(M+msin2α)]
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Single Correct
141 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Multiple Correct
25 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.3
24 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
A small particle of mass m=2kg moving with constant horizontal velocity u=10m/s strikes a wedge shaped block of mass M=4kg placed on smooth horizontal surface on its inclined surface as shown in figure. After collision particle starts moving up the inclined plane. Calculate the velocity of wedge immediately after collision.
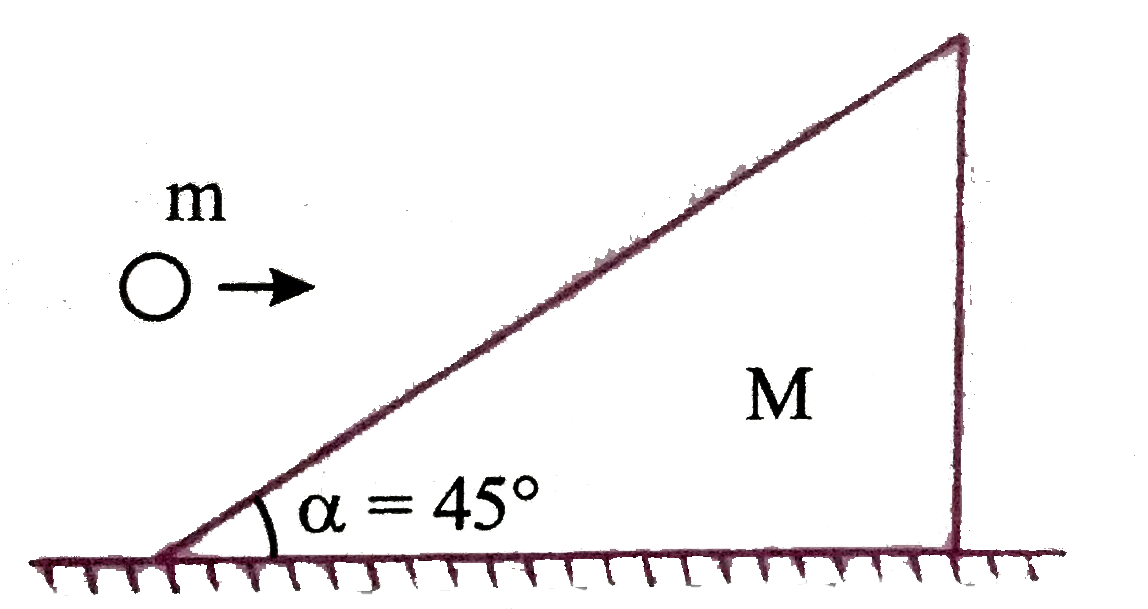
View SolutionA particle of mass m moving horizontal with v0 strikes a smooth wedge of mass M, as shown in figure. After collision, the ball starts moving up the inclined face of the wedge and rises to a height h.
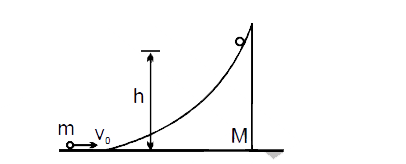
The final velocity of the wedgev2 is
View SolutionA particle of mass m moving horizontal with v0 strikes a smooth wedge of mass M, as shown in figure. After collision, the ball starts moving up the inclined face of the wedge and rises to a height h.
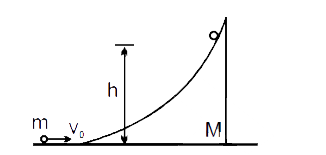
Choose the correct statement related to the wedge M
View SolutionA particle of mass m moving horizontal with v0 strikes a smooth wedge of mass M, as shown in figure. After collision, the ball starts moving up the inclined face of the wedge and rises to a height h.
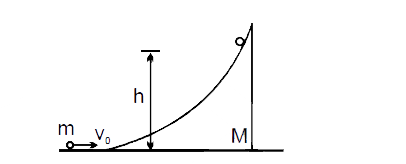
The maximum height h attained by the particle is
View SolutionA particle of mass m moving horizontal with v0 strikes a smooth wedge of mass M, as shown in figure. After collision, the ball starts moving up the inclined face of the wedge and rises to a height h.
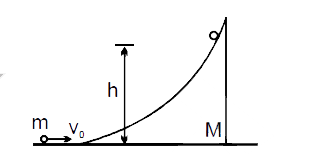
Choose the correct statement(s) related to particle m
View SolutionA particle of mass m moving horizontal with v0 strikes a smooth wedge of mass M, as shown in figure. After collision, the ball starts moving up the inclined face of the wedge and rises to a height h.
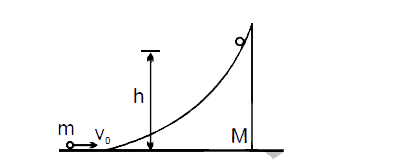
When the particle has risen to a height h on the wedge, then choose the correct alternative(s)
View SolutionA particle of mass m moving horizontal with v0 strikes a smooth wedge of mass M, as shown in figure. After collision, the ball starts moving up the inclined face of the wedge and rises to a height h.
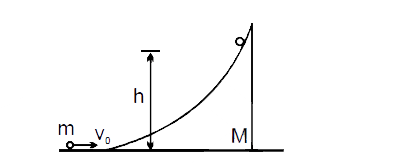
Identify the correct statement(s) related to the situation when the particle starts moving downward
View SolutionA particle of mass m moving horizontal with v0 strikes a smooth wedge of mass M, as shown in figure. After collision, the ball starts moving up the inclined face of the wedge and rises to a height h.
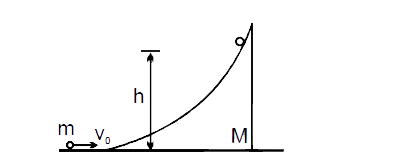
Suppose the particle when reaches the horizontal surfaces, its velocity with respect to ground is v1 and that of wedge is v2. Choose the correct statement (s)
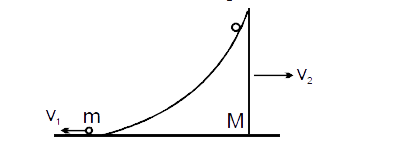
View SolutionA ball of mass m moving horizotally which velocity u hits a wedge of mass M. The wedge is situated on a smooth horizontal source. If after striking with wedge the ball starts moving in vertical direction and the wedge starts moving in horizotal plane. calculate
a. the velocity of wedge V.
b. the velocity (v) at which the ball moves in vertical direction.
c. the impulse imparted by the ball on the wedge.
d. the coefficient of restitution e=?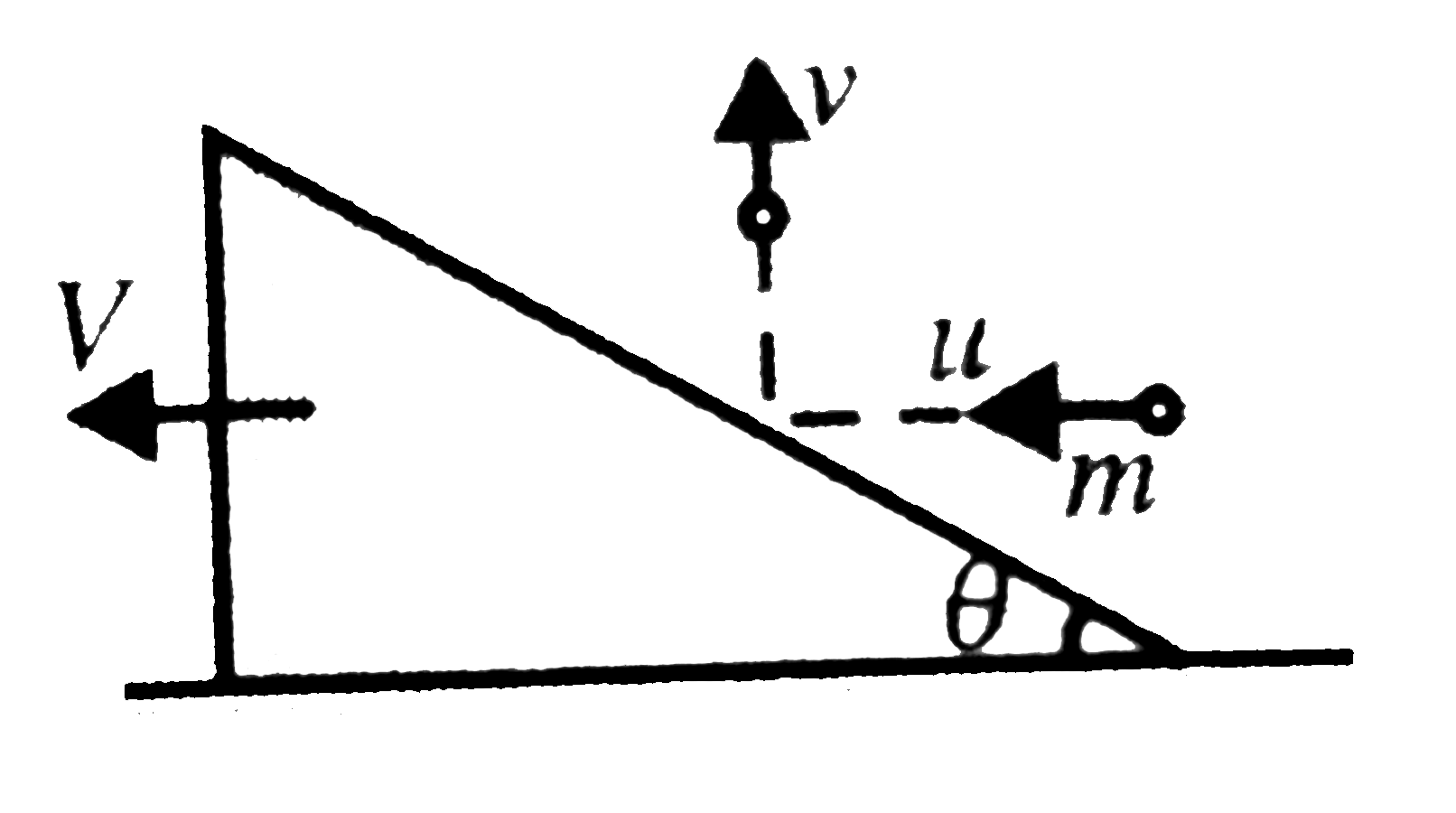
View SolutionA ball of mass m moving horizotally which velocity u hits a wedge of mass M. The wedge is situated on a smooth horizontal source. If after striking with wedge the ball starts moving in vertical direction and the wedge starts moving in horizotal plane. calculate
a. the velocity of wedge V.
b. the velocity (v) at which the ball moves in vertical direction.
c. the impulse imparted by the ball on the wedge.
d. the coefficient of restitution e=?
View Solution
