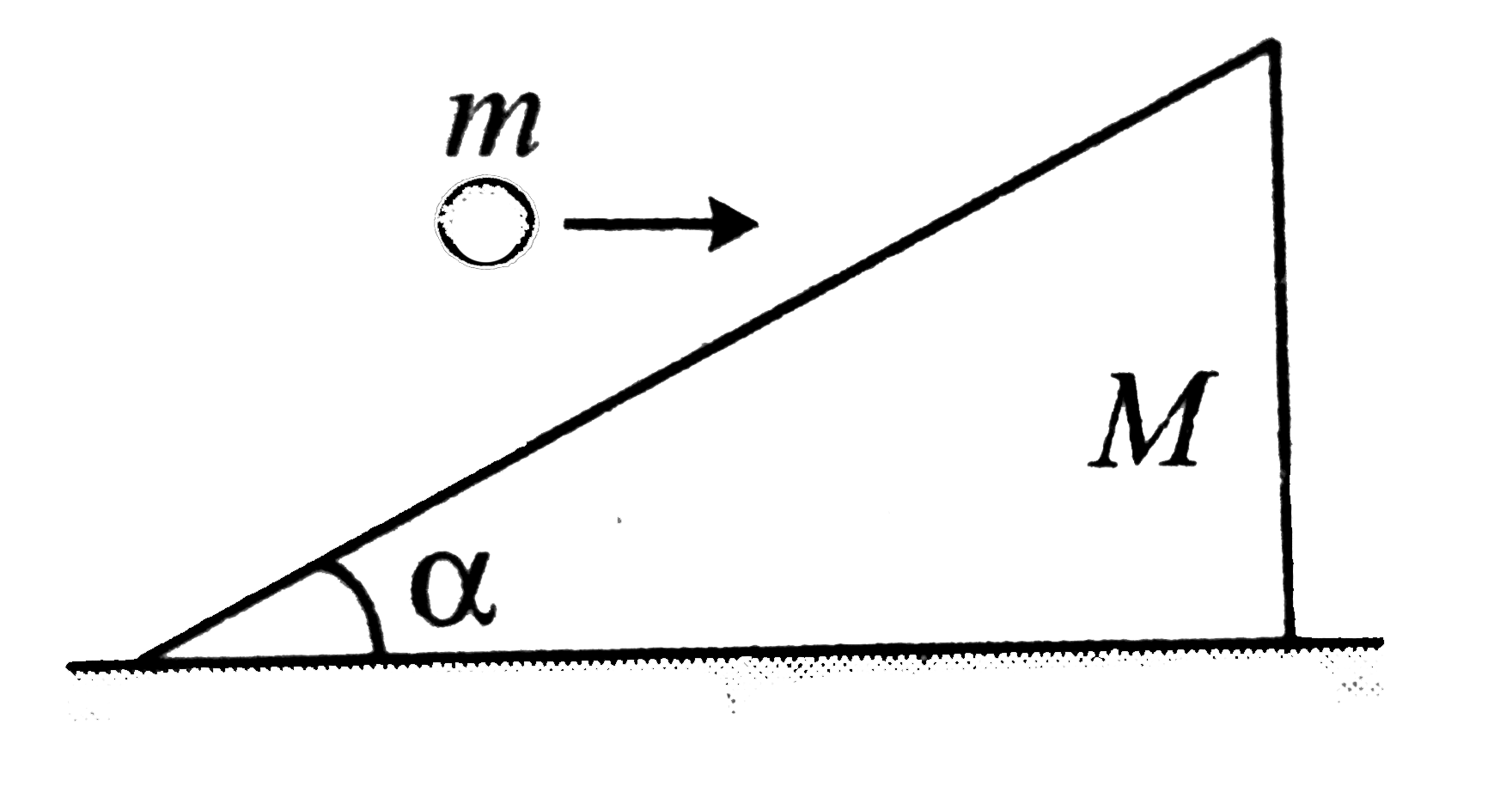
A ball of mass m moving with constant horizontal velocity u strikes a stationary wedge of mass M on its inclined surface as shown in the figure. After collision, the ball starts moving up the inclined plane. The wedge is placed on frictionless horizontal surface.
a. Calculate the velocity of wedge immediately after collision.
b. Calculate the maximum height the ball can ascend on the wedge.
The correct Answer is:musin2αM+msin2α)
a. Let after collision velocity of wedge be V and that of ball be v0 as shown v0 is w.r.t. wedge. Applying conservation of lienar momentum along x-axis, we get
μ=Mv+m(V+v0cosα)….i
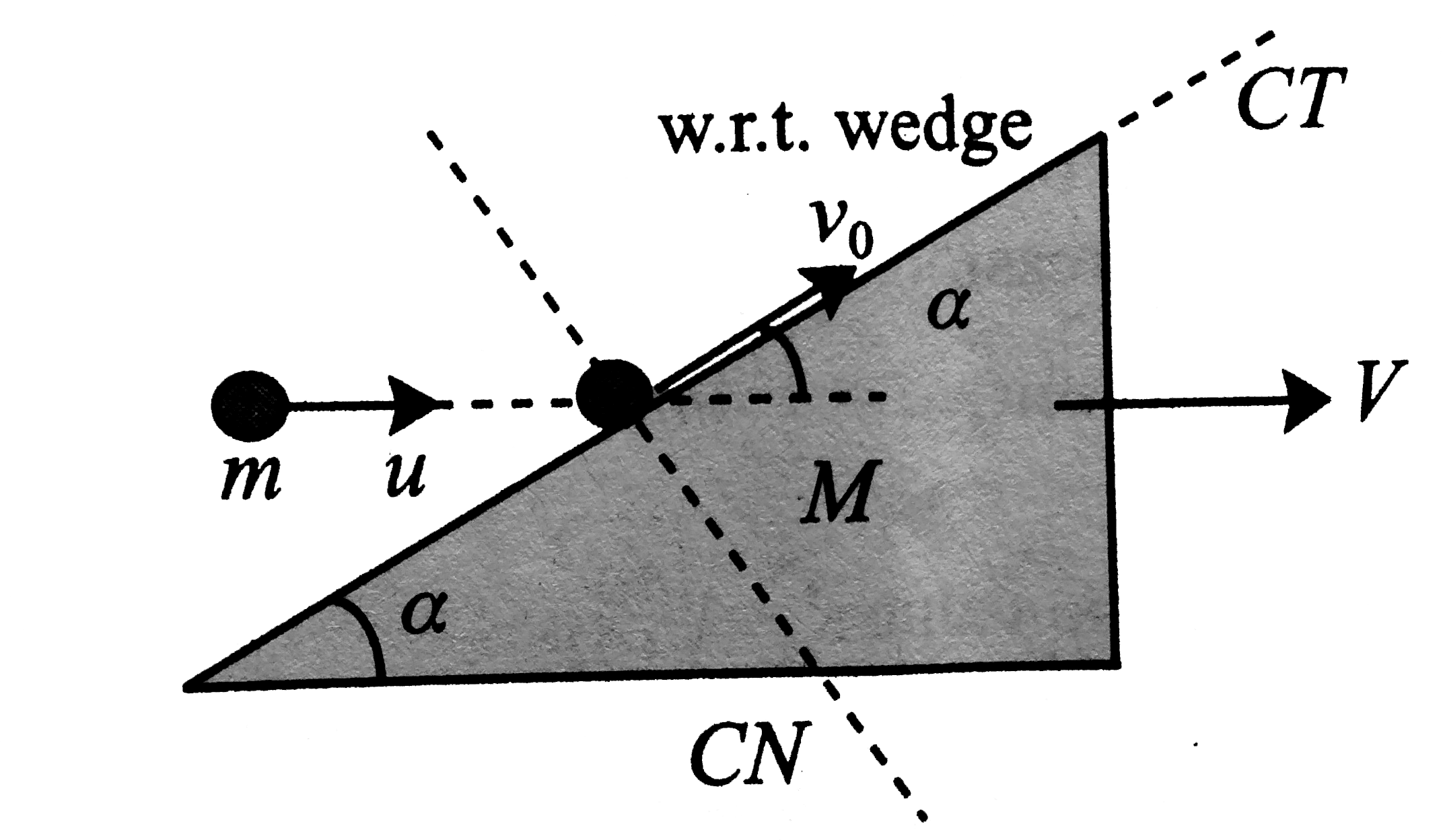
Velocity along CT remains, constant
ucosα=v0+Vcosα.......ii
→vb=(v0cosα+V)ˆi+(v0sinα)ˆj
From i and ii
mu=MV+mV+mcosα(ucosα−Vcosα)
=(M+m)V+μcos2α−mcos2α
⇒V=musin2αM+msin2α
b. When the bal ascends maximum height, then ball will be at rest w.r.t. wedge and ther velocity will be same. Let their common velocity be v'. From conservationof momentum we cn find this common velocity as 'v'=mu(M+m).
From ii v0−(u−V)cosα, put the value of V in this to get
v0=MucosαM+msin2α
Also, v0cosα+V=[Mcos2α+msin2αM+msin2α]u
To find maximum height
From energy conservation
mgh+12(m+M)v'2
=12MV2+12m(v0cosα+V)2+12m(v0sinα)2
2mgh+m2u2M+m=MV2+m(v0cosα+V)2+m(v0sinalpa)2
2mgh+m2u2M+m
Mm2u2sin4α+m(Mcos2α+msin2α)2u2
=+mM2u2cos2αsin2α(M+msin2α)2
Solve to get: h=u22g[M2cos2α(M+m)(M+msin2α)]
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Single Correct
141 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Multiple Correct
25 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.3
24 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
A ball of mass m moving horizotally which velocity u hits a wedge of mass M. The wedge is situated on a smooth horizontal source. If after striking with wedge the ball starts moving in vertical direction and the wedge starts moving in horizotal plane. calculate
a. the velocity of wedge V.
b. the velocity (v) at which the ball moves in vertical direction.
c. the impulse imparted by the ball on the wedge.
d. the coefficient of restitution e=?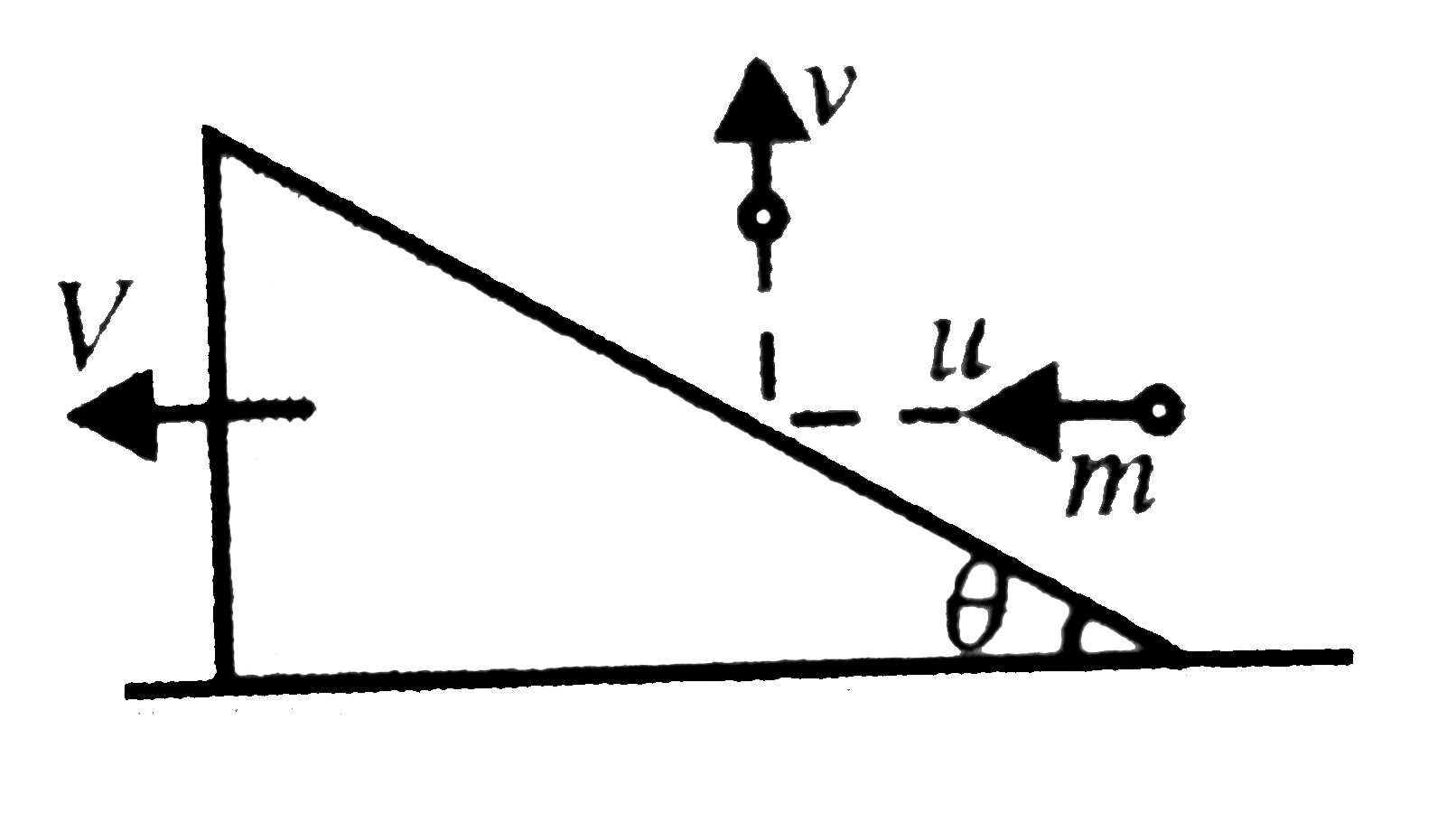
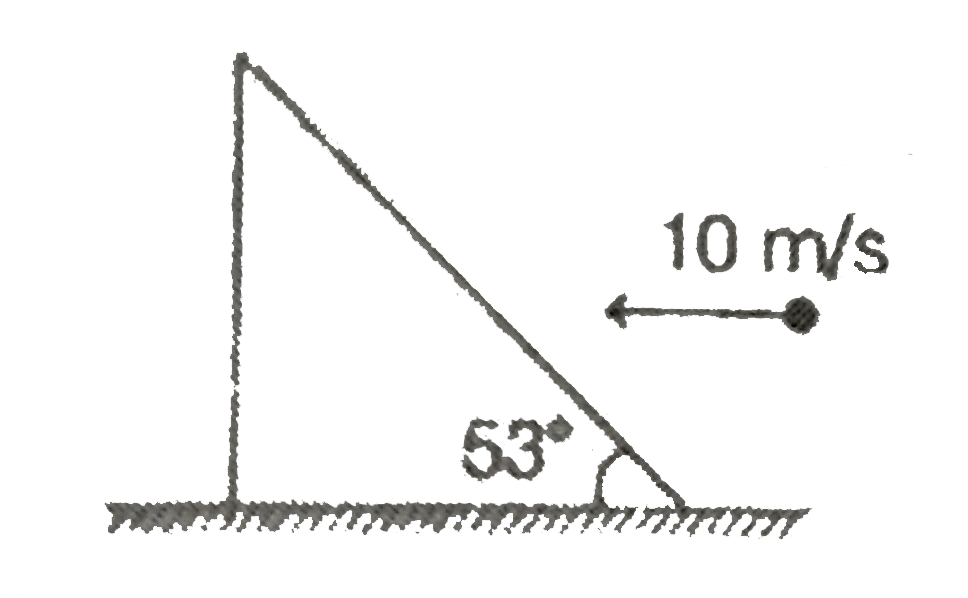
View SolutionA ball mass 2 kg moving horizontally with velocity 10 m/s hits a wedge of mass 5 kg placed on a horizontal surface as shown in the figure. Just after collision klvelocity of wedge is 3.2 m/s. There is no friction at any contact surface. Then (take sin 30∘=3/5)
View SolutionA block of mass 2kg slides down the face of a smooth 45∘ wedge of mass 9kg as shown in the figure. The wedge is placed on a frictionless horizontal surface. Determine the acceleration of the wedge.

View SolutionA ball of mass m collides with a stationary wedge of mass M, perpendicular to its inclined face, inclined at an angle as shown in the figure. If the coefficient of restitution between the wedge and ball is e, calculate the ratio of modulus of velocity of the ball immediately after and before collision. Also calculate the velocity of wedge just after collision.

View SolutionA block of mass m rests on a stationary wedge of mass M. The wedge can slide freely on a smooth horizontal surface as shown in figure. If the block starts from rest

View SolutionA small ball of mass m is projected with a minimum horizontal velocity v0 on a smooth wedge of mass M so that it will reach the highest point of the wedge. Find the value of v0

View SolutionA ball of mass 'm' moving with a horizontal velocity 'v' strikes the bob of mass 'm' of a pendulum at rest. During this collision, the ball sticks with the bob of the pendulum. The height to which the combined mass raises is (g = acceleration due to gravity).
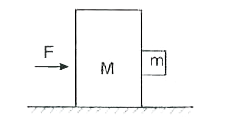
View SolutionA horizontal force F pushes wedge of mass M on a smooth horizontal surface. A block of mass m is stationary to the wedge, then:
View SolutionA heavy ball of mass 2M moving with a velocity v0 collides elastically head on with a cradle of three identical ball each of mass M as shown in figure. Determine the velocity of each ball after collision.

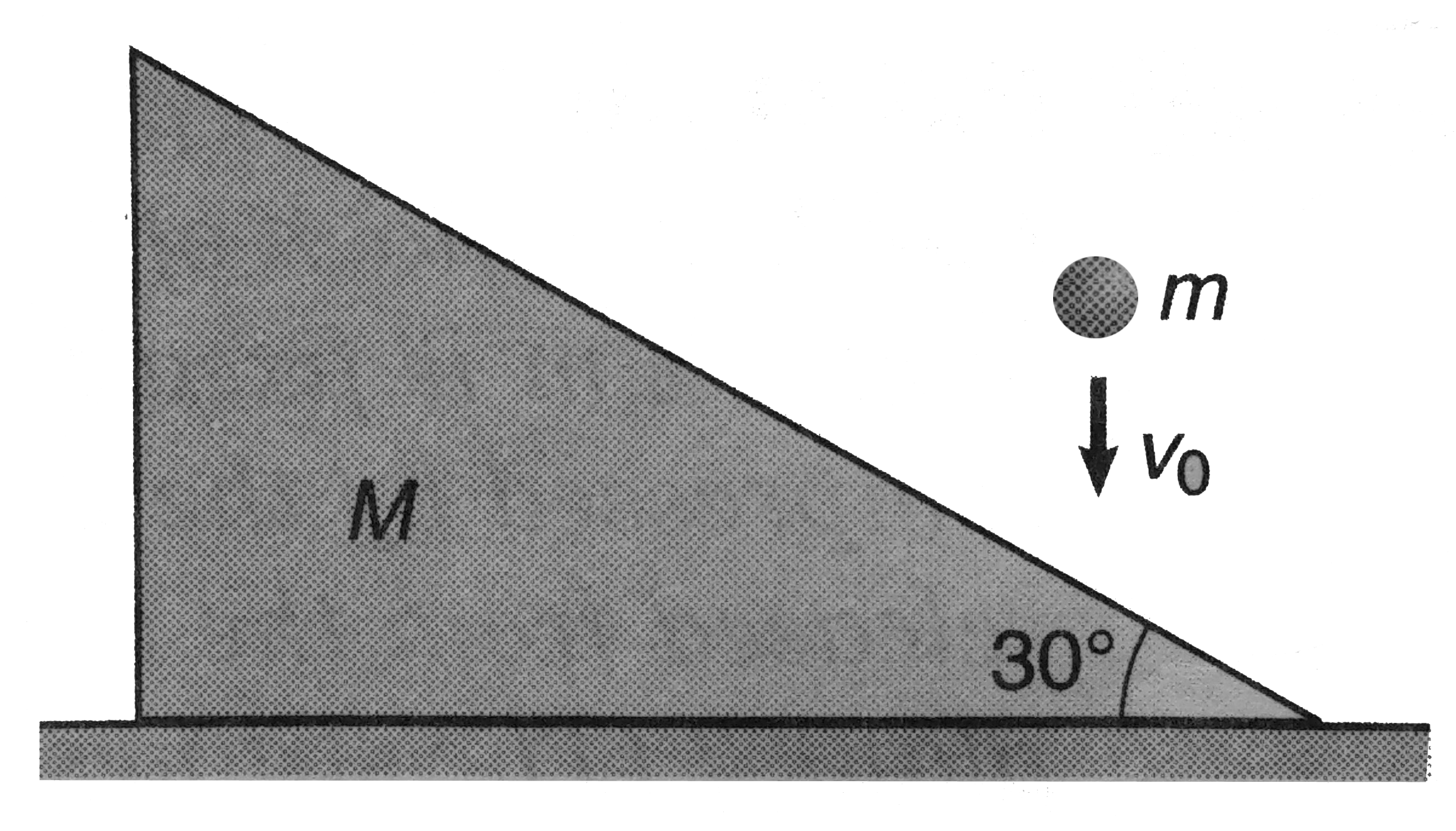
View SolutionA ball of mass m=1kg falling vertically with a velocity v0=2m/s strikes a wedge of mass M=2kg kept on a smooth, horizontal surface as shown in figure. If impulse between ball and wedge during collision is J. Then make two equations which relate J with velocity components of wedge and ball. Also find impulse on wedges from ground during impact.
View Solution
