A ball strikes a smooth horizontal floor obliquely and rebounds inelastically.
The kinetic energy of the ball just after hitting the floor is equal to the potential energy of the ball at its maximum height alter rebound.
Total energy of the ball is not conserved.
The angle of rebound with the vertical is greater than the angle of incidence.
None of the above.
The correct Answer is:B, C
To solve the problem of a ball striking a smooth horizontal floor obliquely and rebounding inelastically, we will analyze the situation step by step.
1. Understanding the Collision:
- The ball strikes the floor at an angle, which means it has both horizontal and vertical components of velocity.
- The collision is inelastic, meaning that the ball does not retain all of its kinetic energy after the collision.
2. Coefficient of Restitution:
- The coefficient of restitution (e) is defined as the ratio of the relative velocity of separation to the relative velocity of approach.
- Since the collision is inelastic, the coefficient of restitution will be between 0 and 1 (0 < e < 1).
3. Kinetic Energy Before and After Collision:
- Before the collision, the kinetic energy (KE) of the ball can be expressed as:
KEinitial=12mu2
- After the collision, the kinetic energy will be:
KEfinal=12mv2
- Due to the inelastic nature of the collision, some kinetic energy is transformed into other forms of energy (like sound, heat, etc.), so:
KEfinal<KEinitial
4. Potential Energy at Maximum Height:
- After rebounding, the ball will rise to a maximum height where its kinetic energy is converted into potential energy (PE). The potential energy at the maximum height (h) is given by:
PE=mgh
- Since some kinetic energy is lost during the collision, the kinetic energy just after hitting the floor will not equal the potential energy at the maximum height.
5. Conservation of Energy:
- The total mechanical energy of the ball (kinetic + potential) is not conserved in this case because some energy is lost during the inelastic collision. Therefore, the statement that the total energy of the ball is conserved is incorrect.
6. Angles of Incidence and Rebound:
- The angle of incidence (α) is the angle at which the ball strikes the floor, and the angle of rebound (β) is the angle at which it leaves the floor.
- In an inelastic collision, the angle of rebound is typically greater than the angle of incidence due to the loss of energy and the change in momentum direction.
Conclusion:
Based on the analysis:
- Option A is incorrect because the kinetic energy just after hitting the floor is not equal to the potential energy at the maximum height after rebound.
- Option B is correct because the total energy of the ball is not conserved during the inelastic collision.
- Option C is correct because the angle of rebound is greater than the angle of incidence in an inelastic collision.
- Option D is incorrect as there are correct options (B and C).
Final Answer:
The correct options are B and C.
---
- The ball strikes the floor at an angle, which means it has both horizontal and vertical components of velocity.
- The collision is inelastic, meaning that the ball does not retain all of its kinetic energy after the collision.
- The coefficient of restitution (e) is defined as the ratio of the relative velocity of separation to the relative velocity of approach.
- Since the collision is inelastic, the coefficient of restitution will be between 0 and 1 (0 < e < 1).
- Before the collision, the kinetic energy (KE) of the ball can be expressed as:
KEinitial=12mu2
- After the collision, the kinetic energy will be:
KEfinal=12mv2
- Due to the inelastic nature of the collision, some kinetic energy is transformed into other forms of energy (like sound, heat, etc.), so:
KEfinal<KEinitial
- After rebounding, the ball will rise to a maximum height where its kinetic energy is converted into potential energy (PE). The potential energy at the maximum height (h) is given by:
PE=mgh
- Since some kinetic energy is lost during the collision, the kinetic energy just after hitting the floor will not equal the potential energy at the maximum height.
- The total mechanical energy of the ball (kinetic + potential) is not conserved in this case because some energy is lost during the inelastic collision. Therefore, the statement that the total energy of the ball is conserved is incorrect.
- The angle of incidence (α) is the angle at which the ball strikes the floor, and the angle of rebound (β) is the angle at which it leaves the floor.
- In an inelastic collision, the angle of rebound is typically greater than the angle of incidence due to the loss of energy and the change in momentum direction.
Based on the analysis:
- Option A is incorrect because the kinetic energy just after hitting the floor is not equal to the potential energy at the maximum height after rebound.
- Option B is correct because the total energy of the ball is not conserved during the inelastic collision.
- Option C is correct because the angle of rebound is greater than the angle of incidence in an inelastic collision.
- Option D is incorrect as there are correct options (B and C).
The correct options are B and C.
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning
2 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Linked Comprehension
105 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Single Correct
141 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
In the figure shown, a particle P strikes the inclined smooth plane horizontally and rebounds vertically. If the angle θ is 60∘ then the coefficient of restitution is:

View SolutionA ball of mass m=1kg strikes a smooth horizontal floor as shown in figure. The impulse exerted on the floor is

View SolutionA ball strikes a smooth horizontal ground at an angle of 45∘ with the vertical. What cannot be the possible angle of its velocity with the vertical after the collision. (Assume e ≤ 1).
View SolutionA particle strikes a smooth horizontal surface at an angle θ>0 and it rebounds at an angle ϕ as shown

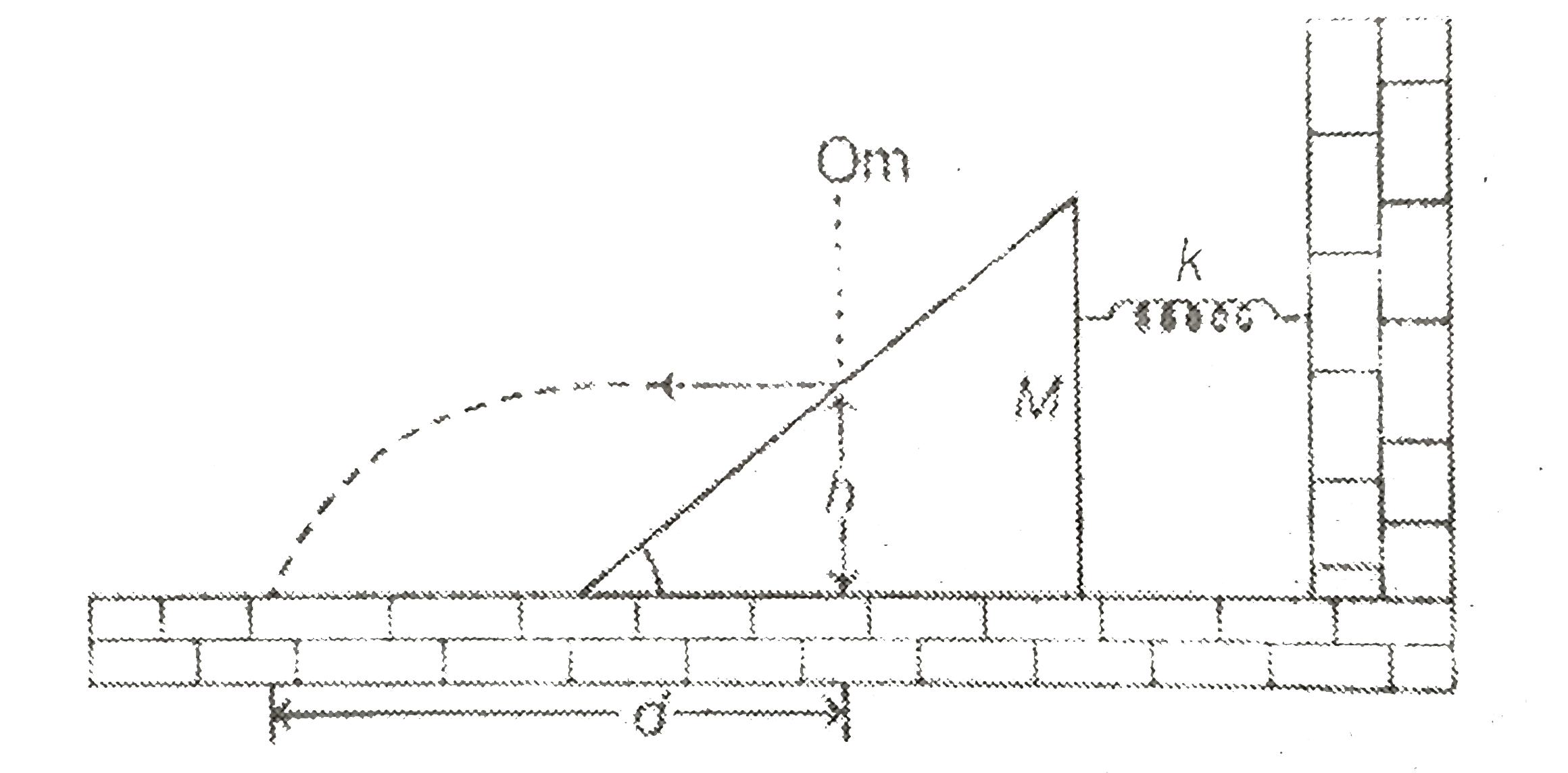
View SolutionA ball of mass m when dropped from certain height as shown in diagram, strikes a wedge kept on smooth horizontal surface and move horizontally just after impact. If the ball strikes the ground at a distance d from its initial line of fall, thenthe amplitude of oscillation of wedge after being hit by the ball will be
View SolutionA uniform plank is resting over a smooth horizontal floor and is pulled by applying a horizontal force at its one end. Which of the following statements are not correct?
View SolutionA uniform plank is resting over a smooth horizontal floor and is pulled by applying a horizontal force at its one end. Which of the following statements are not correct?
View SolutionA particle strikes a smooth horizontal surface at an angle of 45∘ with a velocity of 100m/s and rebounds. If the coefficient of restitution between the floor and the particle is 0.57 then the angle which the velocity of the particle after it rebounds will make with the floor is
View SolutionA girl throws a ball with an initial velocity v at an angle 45∘. The ball strikes a smooth vertical wall at a horizontal distance d from the girl and after rebound returns to her hands. What is the coefficient of restitution between wall and ball ? (v2>dg)
View SolutionA girl throws a ball with initial velocity v at an inclination of 45∘. The ball strikes a smooth vertical wall at a horizontal distance d from the girl and after rebounding returns to her hand. What is the coefficient restitution between the all and the ball ?
View Solution
