A bar magnet is oscillating in the earth's magnetic field with a time period T. If the mass is increased four times, then its time period will be:
The correct Answer is:B
To solve the problem, we need to analyze how the time period of a bar magnet oscillating in a magnetic field changes when its mass is increased.
1. Understanding the Time Period of a Bar Magnet:
The time period T of a bar magnet oscillating in a magnetic field is given by the formula:
T∝√Im
where I is the moment of inertia and m is the mass of the magnet.
2. Moment of Inertia of a Bar Magnet:
For a bar magnet, the moment of inertia I about its center is given by:
I=ml23
However, for oscillations, we can consider the effective moment of inertia in terms of the mass and length.
3. Effect of Increasing Mass:
If the mass of the bar magnet is increased four times, we can denote the new mass as:
m′=4m
4. New Time Period Calculation:
The new time period T′ can be expressed in terms of the original time period T:
T′∝√Im′
Substituting m′=4m:
T′∝√I4m=√14⋅√Im=12√Im
5. Relating New Time Period to Original:
Since T∝√Im, we can write:
T′=2T
6. Conclusion:
Therefore, when the mass of the bar magnet is increased four times, the new time period T′ becomes:
T′=2T
Final Answer:
The new time period will be 2T.
The time period T of a bar magnet oscillating in a magnetic field is given by the formula:
T∝√Im
where I is the moment of inertia and m is the mass of the magnet.
For a bar magnet, the moment of inertia I about its center is given by:
I=ml23
However, for oscillations, we can consider the effective moment of inertia in terms of the mass and length.
If the mass of the bar magnet is increased four times, we can denote the new mass as:
m′=4m
The new time period T′ can be expressed in terms of the original time period T:
T′∝√Im′
Substituting m′=4m:
T′∝√I4m=√14⋅√Im=12√Im
Since T∝√Im, we can write:
T′=2T
Therefore, when the mass of the bar magnet is increased four times, the new time period T′ becomes:
T′=2T
The new time period will be 2T.
Similar Questions
A bar magnet is oscillating in the earth's magnetic field with a period T. What happens to its period and motion if its mass is quadrupled
View SolutionA mass M is suspended from a spring of negiliglible mass the spring is pulled a little and then released so that the mass executes simple harmonic oscillation with a time period T If the mass is increases by m the time period because (54T),The ratio of mM is
View SolutionA bar magnet oscillates in a region of uniform magnetic field with time period T . Now , a piece of wood identical in all respects in terms of mass and length is joined with bar magnet as shown . The new time period of oscillation is
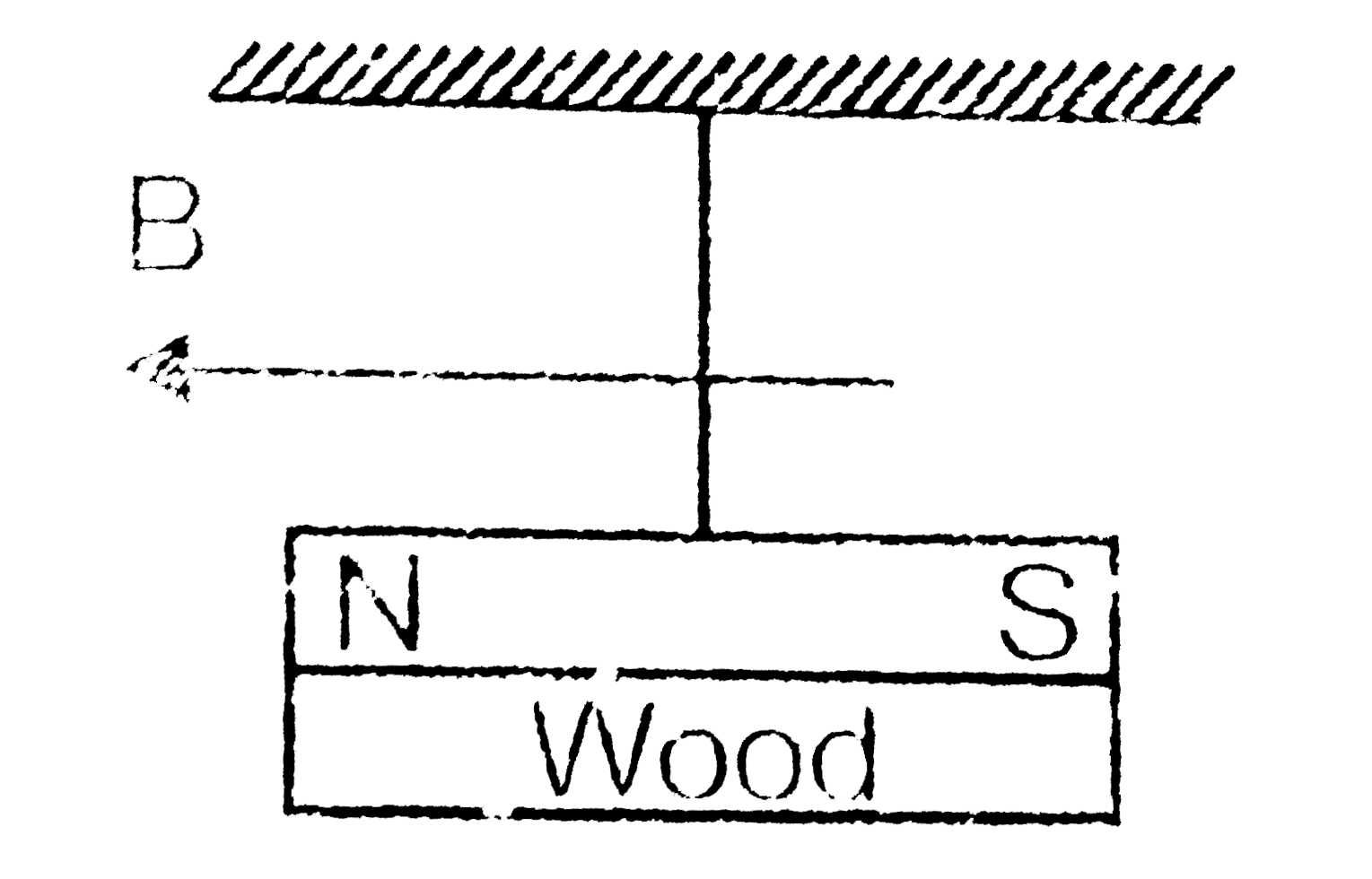 View Solution
View SolutionA bar magnet suspended freely in a uniform magnetic field is vibrating with a time period of 3s. If the field strength is increased to 4 times of the earlier field strength, then the time period (in second) will be
View SolutionA body of mass m attached to a spring which is oscillating with time period 4 s. If the mass of the body is increased by 4 kg, its time period increases by 2 s. Determine value of initial mass m.
View SolutionTime period of a bar magnet oscillating in earth's magnetic field is T. Its magnetic moment is M. Now, a bar magnet of magnetic moment 2M is brought near it. The new time period will be
View SolutionIf a charged particle is a plane perpendicular to a uniform magnetic field with a time period T Then
View SolutionA magnetic needle is made to vibrate in uniform field H, then its time period is T. If it vibrates in the field of intensity 4H, its time period will be
View SolutionA thin magnetic needle oscillates in a horizontal plane with a period T. It is broken into n equals parts. The time period of each part will be
View SolutionPeriod of oscillation of a bar magnet in earth's magnetic field is T . If its mass is reduced to one - fourth of the original mass , maintaining all other parameters same , the new time period will be
View Solution

