A beam of light converges to a point P.A lens is placed in the path of the convergent beam 12cm from P. At what point does the beam converge if the lens is
(a) a convex lens of focal length 20cm. (b) a concave lens of focal length 16cm ?
To solve the problem, we will use the lens formula, which is given by:
1f=1v−1u
Where:
- f is the focal length of the lens,
- v is the image distance from the lens,
- u is the object distance from the lens.
In this case, the object distance u is given as −12cm (negative because the object is virtual and on the same side as the incoming light).
(a) For a convex lens with focal length f=20cm:
1. Identify the values:
- Focal length f=+20cm (positive for convex lens)
- Object distance u=−12cm
2. Substitute into the lens formula:
120=1v−1(−12)
3. Rearranging the equation:
1v=120+112
4. Finding a common denominator:
- The least common multiple of 20 and 12 is 60.
120=360,112=560
1v=360+560=860
5. Calculating v:
v=608=7.5cm
Thus, the beam converges at 7.5cm to the right of the lens.
(b) For a concave lens with focal length f=−16cm:
1. Identify the values:
- Focal length f=−16cm (negative for concave lens)
- Object distance u=−12cm
2. Substitute into the lens formula:
1−16=1v−1(−12)
3. Rearranging the equation:
1v=1−16+112
4. Finding a common denominator:
- The least common multiple of 16 and 12 is 48.
1−16=−348,112=448
1v=−348+448=148
5. Calculating v:
v=48cm
Thus, the beam converges at 48cm to the right of the lens.
Summary of Results:
- (a) For the convex lens, the beam converges at 7.5cm to the right of the lens.
- (b) For the concave lens, the beam converges at 48cm to the right of the lens.
- f is the focal length of the lens,
- v is the image distance from the lens,
- u is the object distance from the lens.
- Focal length f=+20cm (positive for convex lens)
- Object distance u=−12cm
120=1v−1(−12)
1v=120+112
- The least common multiple of 20 and 12 is 60.
120=360,112=560
1v=360+560=860
v=608=7.5cm
- Focal length f=−16cm (negative for concave lens)
- Object distance u=−12cm
1−16=1v−1(−12)
1v=1−16+112
- The least common multiple of 16 and 12 is 48.
1−16=−348,112=448
1v=−348+448=148
v=48cm
- (a) For the convex lens, the beam converges at 7.5cm to the right of the lens.
- (b) For the concave lens, the beam converges at 48cm to the right of the lens.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - NCERT ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Exercise
32 Videos
- NUCLEIBOOK - NCERT ENGLISHCHAPTER - NUCLEIEXERCISE - Exercise
31 Videos
- SEMICONDUCTOR ELECTRONICS MATERIALS DEVICES AND SIMPLE CIRCUITSBOOK - NCERT ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS MATERIALS DEVICES AND SIMPLE CIRCUITSEXERCISE - Exercise
15 Videos
Similar Questions
A beam of light converges at a point P. Now a convex lens is placed in the part of the converngent beam at 15 cm from P. At what point does a beam converge if the convex lens has a focad length 10 cm ?
View SolutionA beam of light converges to a point on a screen S. A mirror is placed in front of the screen at a distance of 10cm form the screen. It is found that the beam now converges at a point 20cm in front of the mirror. Find the focal length of the mirror.
View SolutionA convex lens of focal length A and a concave lens of focal length B are placed in contact. The focal length of the combination is
View SolutionA beam of light converges at a point P. Draw ray diagram to show where the beam will converge if (i) a convex lens and (ii) a concave lens is kept in the path of the beam?
View SolutionA convex lens of focal length 40 cm is in contact with a concave lens of focal length 25 cm. The power of the combination is
View SolutionTwo thin lenses are placed 5cm apart along the same axis and illuminted with a beam of light parallel to that axis. The first lens in the path of the beam is a converging lens of focal length 10cm whereas the second is a diverging lens of focal length 5cm. If the second lens if now moved toward the first, the emergent light
View SolutionWhere should an object be placed from a converging lens of focal length 20 cm, so as to obtain a real image of magnification 2?
View SolutionFigure given below shows a beam of light converging at point P. When a concave lens of focal length 16cm is introduced in the path of the beam at a place O shown by dotted line such that OP becomes the axis of the lens, the beam converges at a distance x from the lens. The value x will be equal to
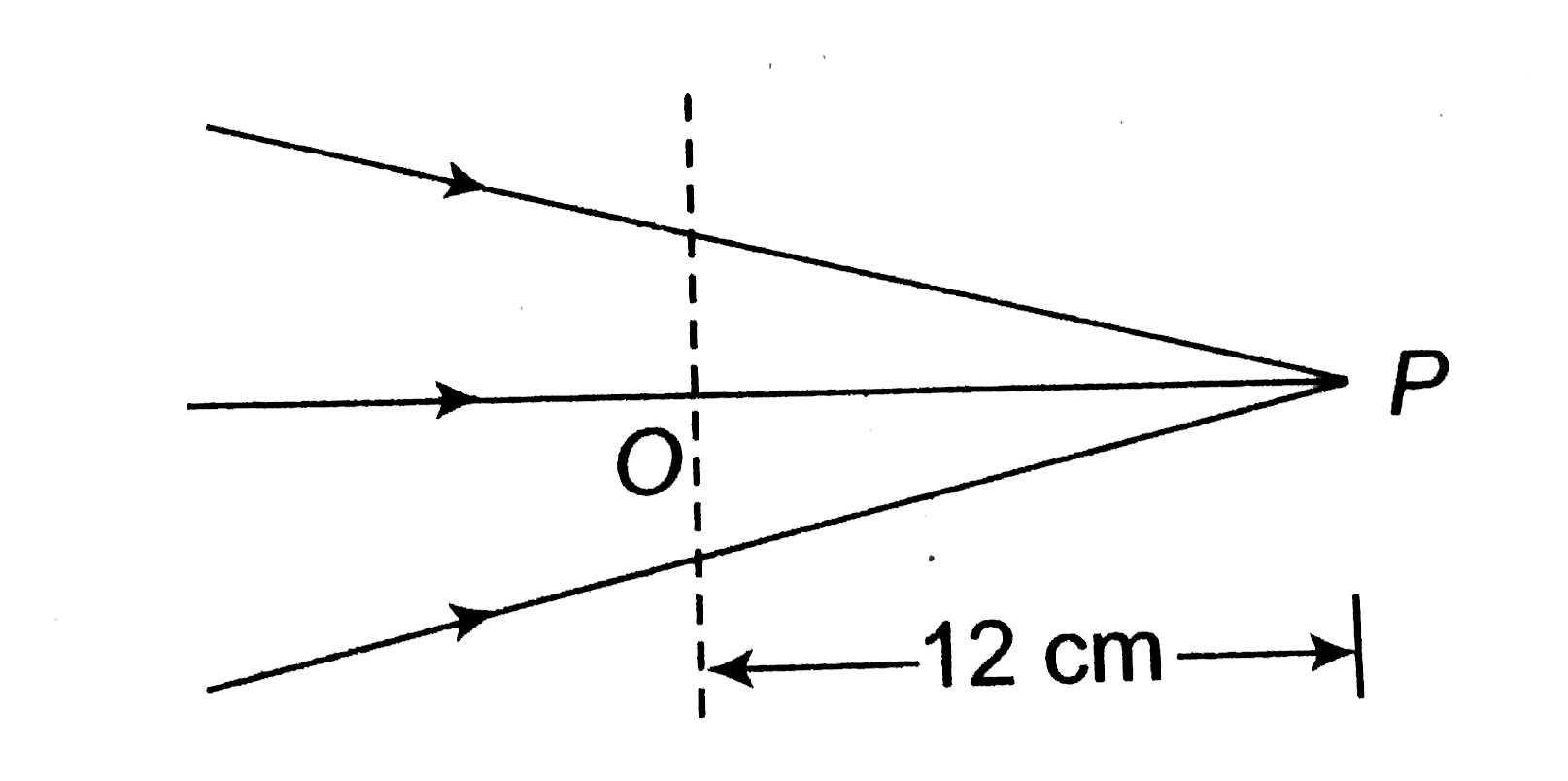
View SolutionA parallel beam of light falls successively on a thin convex lens of focal length 40 cm and then ono a thin convex lens of focal length 10cm as shown in figure.
In figure, the second lens is an equi-concave lens of focal length 10cm and made of a material of refractive index 1.5. In both the cases, the second lens has an aperture equal to 1cm.
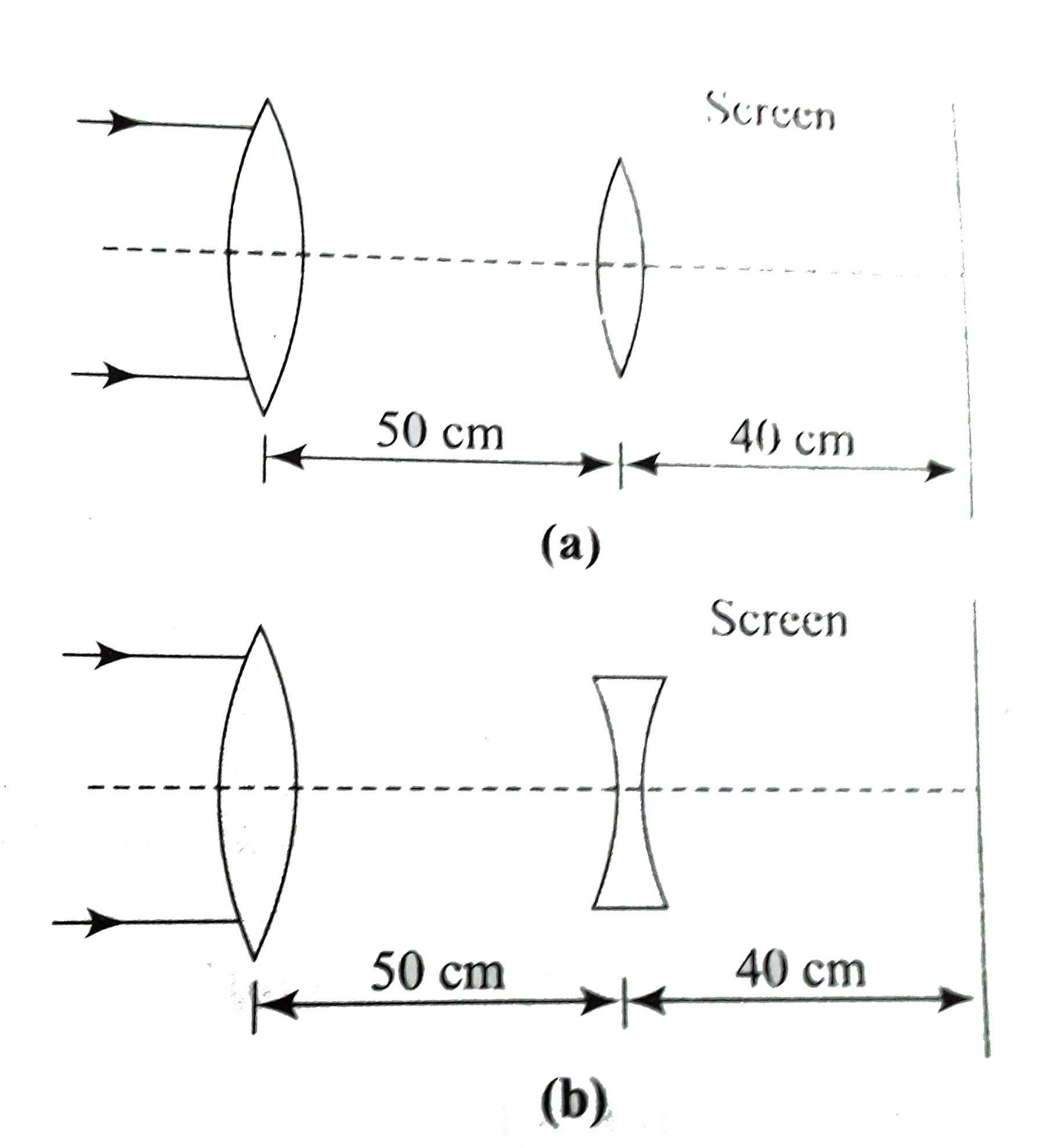
Q. Compare the area illuminated by the beam of light on the screen, which passes through the second lens in the two cases. The ratio (A2/A1) will be
View SolutionA converging beam of light is incident on a concave lens. The beam converges behind the lens at 15 cm from its centre, in the absence of the lens. Select the correct alternative
View Solution
