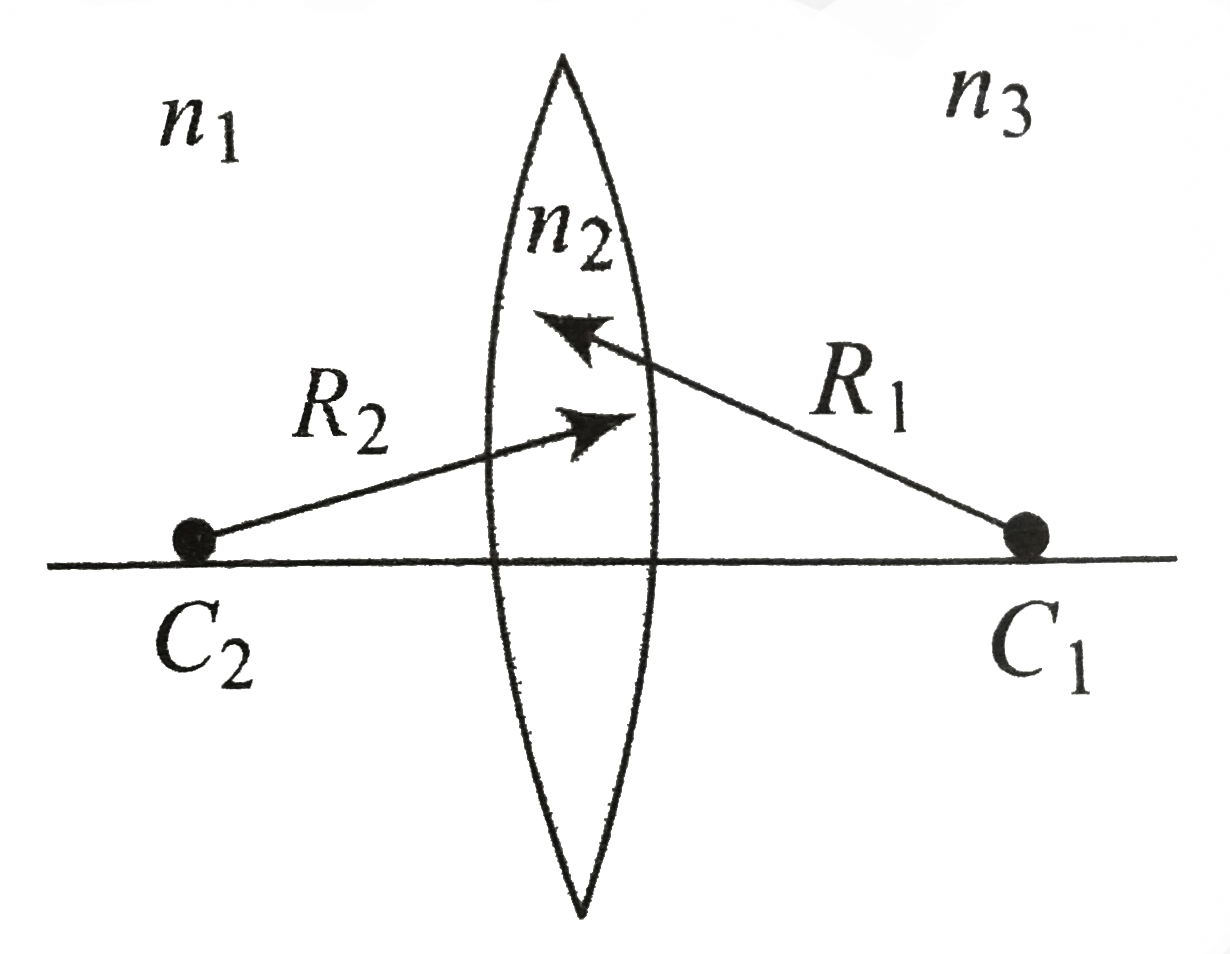
A biconvex lens separates two media of refractive indices 1.3 and 1.7. the refractive index of the lens is 1.5 and the radii of curvature of the two sides of the lens are $r_{1} = 10 c m$ and $r_{2} = 60 c m$ .
The medium of refractive index 1.3 extends to 78 cm from the lens and that of refractive index 1.7 extends of 34 cm from the lens. A luminous object O is at a distance of 144 cm from the lens. Find the position of the final image from the lens.
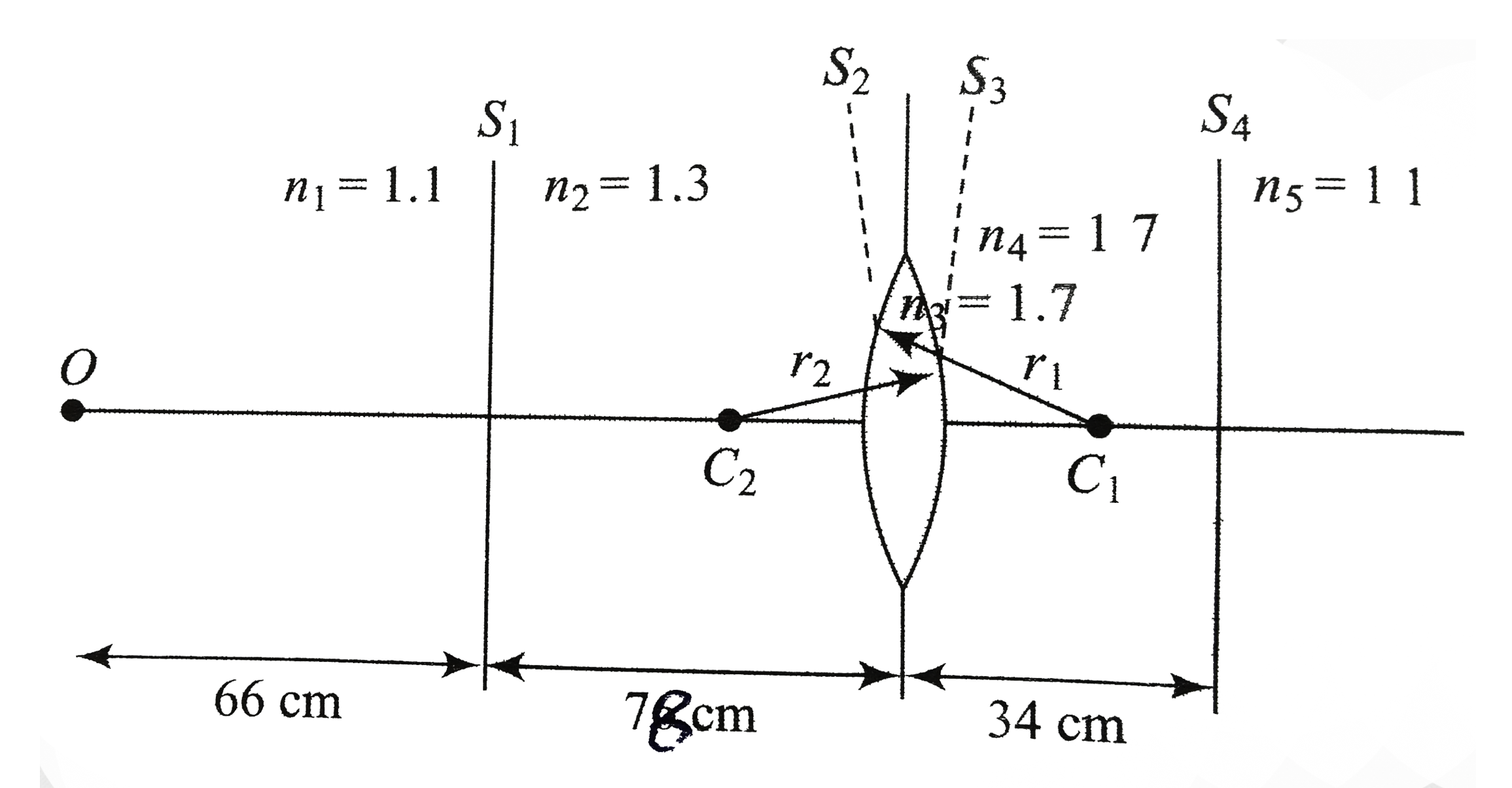
$A biconvex lens separates two media of refractive indices 1.3 and 1.7. the refractive index of the lens is 1.5 and the radii of curvature of the two sides of the lens are r(1)=10cm and r(2)=60cm . The medium of refractive index 1.3 extends to 78 cm from the lens and that of refractive index 1.7 extends of 34 cm from the lens. A luminous object O is at a distance of 144 cm from the lens. Find the position of the final image from the lens.$

Video Solution

Text Solution

Verified by Experts

Once again we have to apply single surface refraction equation to the four surfaces $S_{1}, S_{2}, S_{3}$ and $S_{4}$ . But we have learned the general thin lens equation
$\frac{n_{3}}{v} - \frac{n_{1}}{u}$
$\frac{n_{2} - n_{1}}{R_{1}} + \frac{n_{3} - n_{2}}{R_{2}}$
which will take account of the two refractions at $S_{2}$ and $S_{3}$ . For refraction at surface $S_{1}$ :
$\frac{1.3}{v} - \frac{1.1}{(- 66)} = \frac{(1.3 - 1.1)}{\infty} = 0 \Rightarrow v = - 78 c m$
Image lies to the left of the surface $S_{1}$ . This acts as an object for the lens.
For refraction throught the lens: We apply the general thin lens equation.
Object distance for lens
$u^{'} = - (78 + 78) c m$
$\frac{1.7}{v^{'}} - \frac{1.3}{(- 156)} = \frac{1.5 - 1.3}{+ 10} + \frac{1.7 - 1.5}{(- 60)}$
$v^{'} = 340 c m$
For refraction at surface $S_{4} :$ Object distance for refraction $S_{4}$ is $340 - 34 = 306 c m$
$\frac{1.1}{v^{''}} - \frac{1.7}{(+ 306)} = 0$
$\Rightarrow v^{''} = \frac{1.1 \times 3.6}{1.7} = 198 c m$ to the right of $S_{4}$

Updated on:21/07/2023