The radii of curvature of the two surfaces of a lens are 20 cm and 30 cm and the refractive index of the material of the lens is 1.5. If the lens is concave -convex, then the focal length of the lens is
24 cm
10 cm
15 cm
120 cm
The correct Answer is:D
To find the focal length of a concave-convex lens given the radii of curvature of its two surfaces and the refractive index, we can use the lens maker's formula:
1f=(μ−1)(1R1−1R2)
Where:
- f is the focal length of the lens,
- μ is the refractive index of the lens material,
- R1 is the radius of curvature of the first surface,
- R2 is the radius of curvature of the second surface.
1. Identify the given values:
- R1=20cm (for the first surface, which is convex)
- R2=−30cm (for the second surface, which is concave; note that the radius for a concave surface is taken as negative)
- μ=1.5
2. Substitute the values into the lens maker's formula:
1f=(1.5−1)(120−1−30)
3. Calculate μ−1:
μ−1=1.5−1=0.5
4. Calculate 1R1−1R2:
1R1=120=0.05
1R2=1−30=−130≈−0.0333
1R1−1R2=0.05−(−0.0333)=0.05+0.0333=0.0833
5. Substitute back into the formula:
1f=0.5×0.0833=0.04165
6. Calculate the focal length f:
f=10.04165≈24cm
Final Answer:
The focal length of the lens is approximately 24cm.
- f is the focal length of the lens,
- μ is the refractive index of the lens material,
- R1 is the radius of curvature of the first surface,
- R2 is the radius of curvature of the second surface.
- R1=20cm (for the first surface, which is convex)
- R2=−30cm (for the second surface, which is concave; note that the radius for a concave surface is taken as negative)
- μ=1.5
1f=(1.5−1)(120−1−30)
μ−1=1.5−1=0.5
1R1=120=0.05
1R2=1−30=−130≈−0.0333
1R1−1R2=0.05−(−0.0333)=0.05+0.0333=0.0833
1f=0.5×0.0833=0.04165
f=10.04165≈24cm
The focal length of the lens is approximately 24cm.
Topper's Solved these Questions
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - medical entrance special format question
23 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Medical entrance gallary
76 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Checkpoint 9.7
10 Videos
- NUCLEIBOOK - DC PANDEY ENGLISHCHAPTER - NUCLEIEXERCISE - C MADICAL ENTRANCES GALLERY
46 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective
9 Videos
Similar Questions
The radius of curvature of the convex face of a plano convex lens is 12cm and the refractive index of the material of the lends 1.5. Then, the focal length of the lens is
View SolutionA converging bundle of rays is intercepted by a biconcave lens. The radii of curvature of both surfaces are 20cm and the refractive index of the material of the lens is 1.5. If the rays originially converged to a point 10cm in front of the lens, where will they now converge after passing through the lens?

View Solution
Knowledge Check
The radius of curvature of the curved surface of a plano-convex lens is 20cm. If the refractive index of the material of the lens be 1.5, it will
Aact as a convex lens only for the objects that lie on its curved side.Bact as a concave lens for the objects that lie on its curved side.Cact as a convex lens irrespective of the side on which the object lies.Dact as a concave lens irrespective of side on which the object lies.
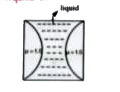
The effective focal length of the lens combination shown in figure is -60 cm. The radius of curvature of the curved surfaces of the plano-convex lenses are 12 cm each and refractive index of the material of the lens is 1.5. The refractive index of the liquid is
View SolutionFind the radius of curvature of the convex surface of a plan-convex lens, whose focal length is 0.3 m and the refractive index of the material of the lens is 1.5.
View SolutionA bicovex lens has radii of cuvature 20 cm each. If the refractive index of the material of the lens is 1.5, what is its focal length?
View SolutionThe radius of curvature of the convex surface of a thin plano-convex lens is 12 cm, and the refractive index of its material is 1.6. What is the power of lens ?
View SolutionThe refractive index of a material of a plano-concave lens is 53, the radius of curvature is 0.3 m. The focal length of the lens in air is
View SolutionThe radii of curvatures of a convex lens are 0.04 m and 0.04m. Its refractive index is 1.5. Its focal length is
View SolutionIf in a planoconvex lens, the radius of curvature of the convex surface is 10cm and the focal length is 30cm, the refractive index of the material of the lens will be
View Solution
