A black metal foil is warmed by radiation from a small sphere at temperature T and at a distance d it is found that the power received by the foil is P If both the temperature and the distance are doubled the power received by the foil will be .
A) 16P
B) 4P
C) 2P
D) P
The correct Answer is:B
To solve the problem, we need to apply the Stefan-Boltzmann law and the inverse square law of radiation. Here’s a step-by-step solution:
Step 1: Understand the Initial Conditions
We have a small sphere at temperature T radiating power P to a black metal foil located at a distance d.
Step 2: Apply the Stefan-Boltzmann Law
According to the Stefan-Boltzmann law, the power received by the black metal foil (which behaves as a perfect black body) is proportional to the fourth power of the absolute temperature of the source.
The power received by the foil can be expressed as:
P∝T4
Step 3: Calculate the New Temperature
If the temperature T is doubled, the new temperature T2 becomes:
T2=2T
Step 4: Calculate the New Power Received
Using the Stefan-Boltzmann law again, the new power P2 received by the foil when the temperature is doubled is:
P2=k(T2)4=k(2T)4=k⋅16T4
Thus, the new power received by the foil is:
P2=16P
Step 5: Consider the Effect of Distance
Now, we also need to consider the effect of distance. If the distance d is doubled, the new distance d2 becomes:
d2=2d
According to the inverse square law, the intensity I of radiation at a distance d from a point source is given by:
I∝Pd2
Step 6: Calculate the New Intensity
The new intensity I2 at distance d2 is:
I2=P2(d2)2=16P(2d)2=16P4d2=4Pd2
Step 7: Final Power Received by the Foil
The power received by the foil is proportional to the intensity and the area of the foil. Since the area remains constant, the new power P2 received by the foil is:
P2=I2⋅A=(4Pd2)⋅A
Step 8: Conclusion
Since the area of the foil does not change, we conclude that the power received by the foil when both the temperature and the distance are doubled is:
P2=4P
Final Answer
Thus, the power received by the foil will be 4P.
---
We have a small sphere at temperature T radiating power P to a black metal foil located at a distance d.
According to the Stefan-Boltzmann law, the power received by the black metal foil (which behaves as a perfect black body) is proportional to the fourth power of the absolute temperature of the source.
P∝T4
If the temperature T is doubled, the new temperature T2 becomes:
T2=2T
Using the Stefan-Boltzmann law again, the new power P2 received by the foil when the temperature is doubled is:
P2=k(T2)4=k(2T)4=k⋅16T4
Thus, the new power received by the foil is:
P2=16P
Now, we also need to consider the effect of distance. If the distance d is doubled, the new distance d2 becomes:
d2=2d
I∝Pd2
The new intensity I2 at distance d2 is:
I2=P2(d2)2=16P(2d)2=16P4d2=4Pd2
The power received by the foil is proportional to the intensity and the area of the foil. Since the area remains constant, the new power P2 received by the foil is:
P2=I2⋅A=(4Pd2)⋅A
Since the area of the foil does not change, we conclude that the power received by the foil when both the temperature and the distance are doubled is:
P2=4P
Thus, the power received by the foil will be 4P.
Topper's Solved these Questions
Similar Questions
A surface at temperature T0K receives power P by radiation from a small sphere at temperature T<T0 and at a distance d. If both T and d are doubled the power received by the surface will become .
View SolutionThe surface temperature of the sun is T0 and it is at average distance d from a planet. The radius of the sun is R. The temperature at which planet radiates the energy is
View SolutionA spherical black body with a radius of 12 cm radiates 450 watt power at 500 K. If the radius were halved and the temperature doubled, the power radiated in watt would be
View SolutionRadiation from a black body at the thermodynamic temperature T1 is measured by a small detector at distance d1 from it. When the temperature is increased to T2 and the distance to d2 , the power received by the detector is unchanged. What is the ratio d2/d1?
View SolutionA spherical black body with radius 12 cm radiates 450 w power at 500 K. If the radius is halved and the temperature doubled, the power radiated in watts would be
View SolutionA spherical black body with radius 12 cm radiates 640 w power at 500 K. If the radius is halved and the temperature doubled, the power radiated in watts would be
View SolutionX-ray from a Coolidge tube is incident on a thin aluminum foil. The intensity of the X-ray transmitted by the foil is found to be I0. The heating current is increased so as to increase the temperature of the filament. The intensity of the X-ray transmitted by the foil will be
View SolutionAn aluminiumum foil of relative emittance 0.1 is placed in between two concentric spheres at temperatures 300K and 200k respectively. Calculate the temperature of the foil after the steady state is reached . Assume that the spheres are perfect black body radiators. Also calculate the rater of energy transfer between one of the spheres and the foil.
[σ=5.67×10−8 S.I. Unit]
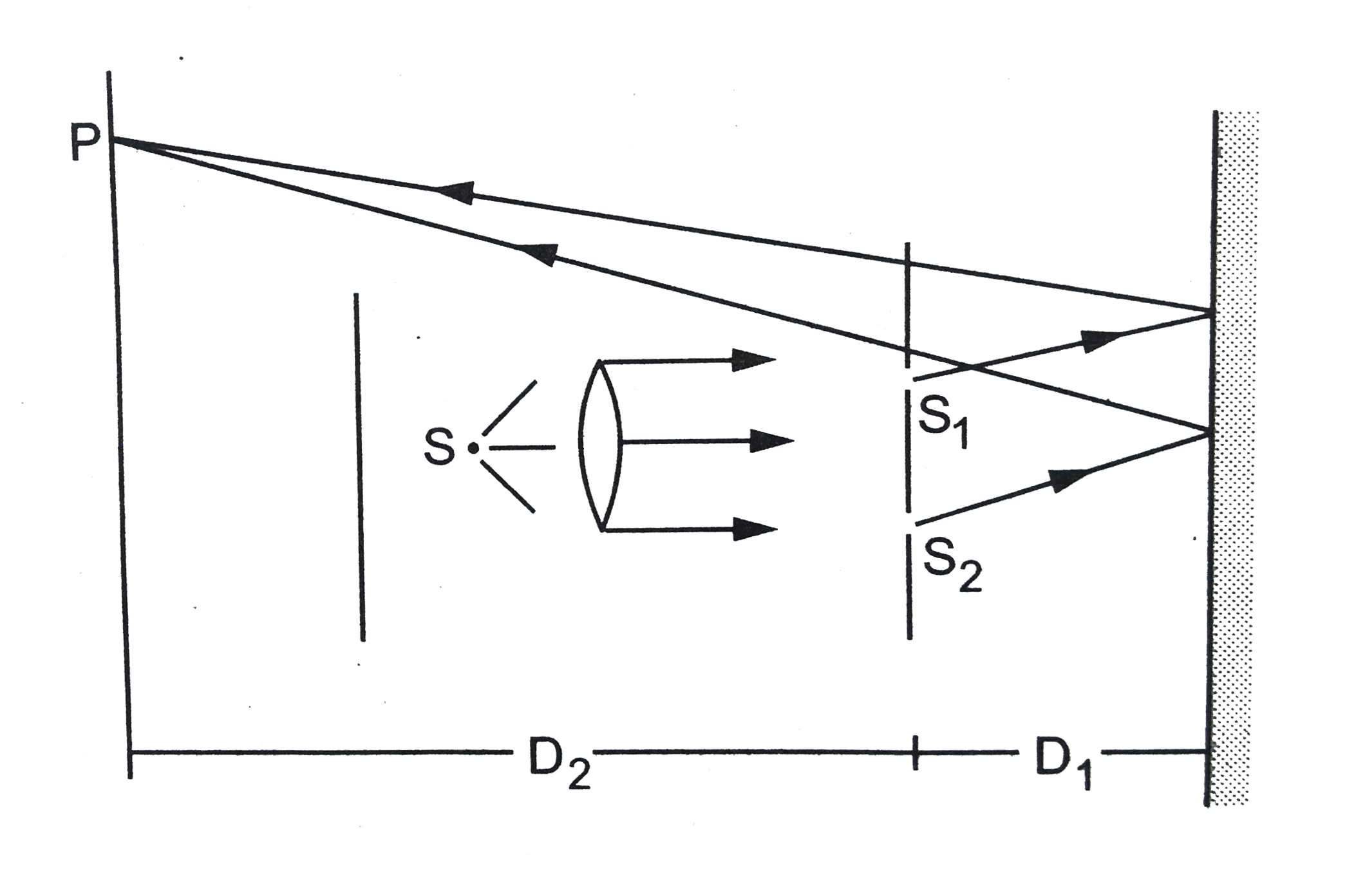
View SolutionA double slit S1−S2 is illuminated by a coherent light of wavelength λ. The slits are separated by a distance d. A plane mirror is placed in front of the double slit at a distance D1, from it and a screen ∑ is placed behind the double slit at a distance D2, from it . The screen ∑ receives only the light reflected by the mirror. Find the fringe-width of the interference pattern on the screen.
View SolutionA point sound source is situated in a medium of dulk modulus 1.6×105N/m2. An observer standing at a distance 10mfrom the source writes down the equeation for the wave as y=Asin(15πx−6000πt). Here y and x are in meter and t is in second. The maximum pressure ampulitude received to the observer's ear is (24π) pa, then find.
(a) the density of the medium,
(b) the displacement ampulitude A of the wave recived by the observer and
(c ) the power of the sound source.
View Solution
