A block A of mass $m_{1}$ is placed on a horizontal frictionless table. It is connected to one end of a light spring of force constant k whose other end is fixed to a wall. A small block B of mass $m_{2}$ is placed on block A. The coefficient of static friction between the blocks is $μ$ . The system is displaced slightly from its equilibrium position and released. What is the maximum amplitude of the resulting simple harmonic motion of the system so that the upper block does not slip over the lower block ?

Video Solution

Text Solution

Verified by Experts

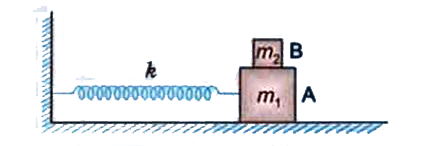
The angular frequency of the system is
$ω = {[\frac{k}{m_{1} + m_{2}}]}^{1 / 2} \dots (i)$
the upper block of mass $m_{2}$ will not slip over the lower block of mass $m_{2}$ if the maximum force on the upper block $f_{max}$ does not exceed the frictional force $μ$ mg between the two blocks. Now
$f_{max} = m a_{max} = m ω^{2} A_{max} ... (i i)$
where $a_{max}$ is the maximum acceleration and $A_{max}$ is the maximum amplitude. Using (i) in (ii),
we get $f_{max} = \frac{m k A_{max}}{(m_{1} + m_{2})}$
for no slippin, $f_{max} = μ m g$
or $\frac{m k A_{max}}{(m_{1} + m_{2})} = μ m g or A_{max} = \frac{μ (m_{1} + m_{2}) g}{k}$

Updated on:21/07/2023