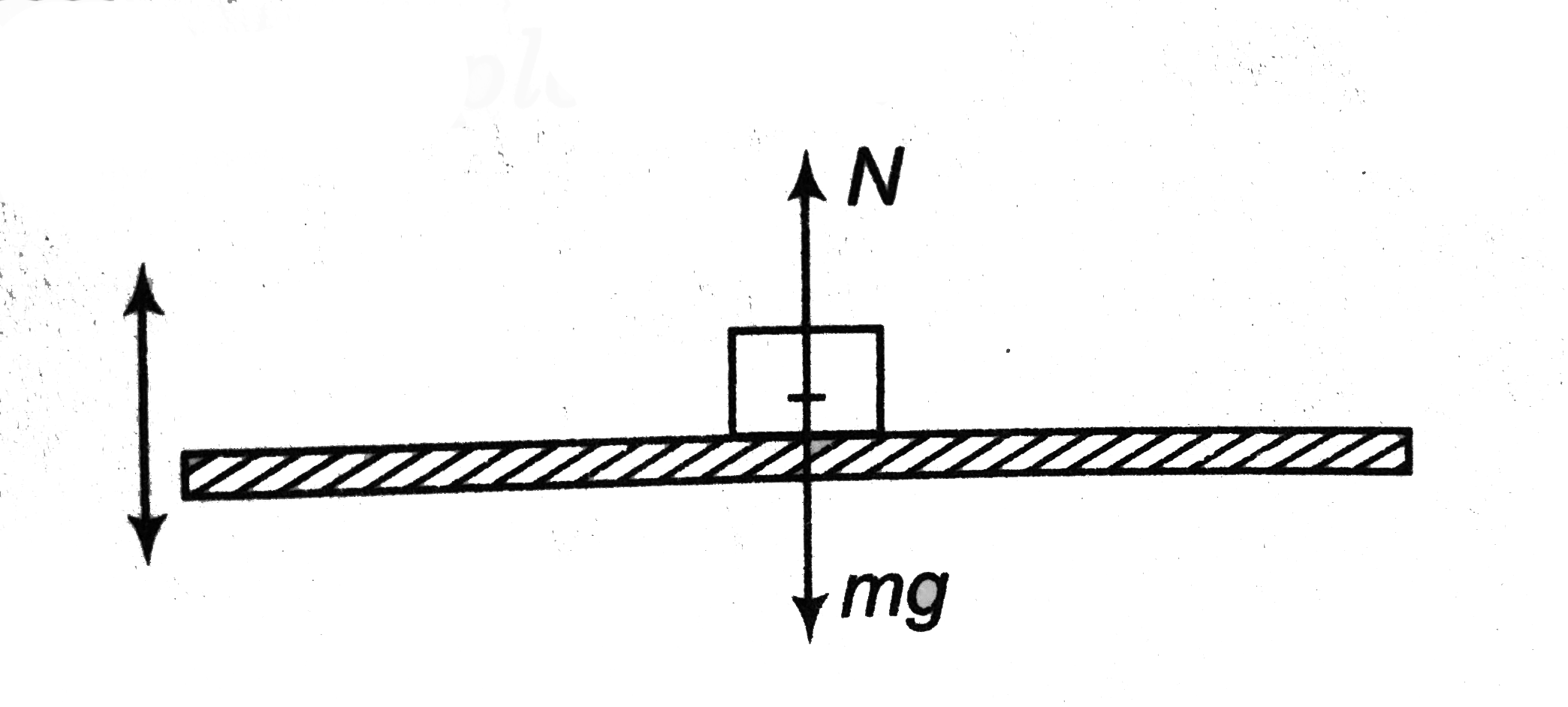
A block is kept is kept over a horizontal platform, executing vertical SHM of angular frequency ω. Find maximum amplitude of oscillations, so that the block does not leave contact with the platform.
The correct Answer is:A
At mean position, acceleration, a=0
⇒N=mg (N = normal reaction)
Below the mean positon, acceleration is upwards (towards the mean position)
∴N−mg=ma or N=m(g+a)
Above the mean position, acceleration is downwards (towards the mean position)
∴mg−N=ma or N=m(g−a)
In this case, N decreases as 'alpha' increases. At the extreme position acceleration is maximum (=ω2A) so N is minimum. When the block leaves contact with the plank N becomes zero.
∴0=m(g−ω2A) or A=gω2
Therfore, the maximum value of amplitude A for not leaving the contact is gω2.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example Type 6
4 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example Type 7
1 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example Type 4
1 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEYCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEYCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
A coin is placed on a horizontal platform which undergoes vertical simple harmonic motion of angular frequency ω. The amplitude of oscillation is gradually increased. The coin will leave contact with the platform for the first time :
View SolutionA coin is placed on a horizontal platform which undergoes vertical simple harmonic motion of angular frequency ω. The amplitude of oscillation is gradually increased. The coin will leave contact with the platform for the first time
View Solution
Knowledge Check
A coin is placed on a horizontal platform which undergoes vertical simple harmonic motion of angular frequency ω. The amplitude of oscillation is gradually increased. The coin will leave contact with the platform for the first time
A(a) at the mean position of the platformB(b) for an amplitude of gω2C(c) for an amplitude of g2ω2D(d) at the highest position of the platformA coin is placed on a horizontal platform which undergoes vertical simple harmonic motion of angular frequency ω. The amplitude of oscillation is gradually increased. The coin will leave contact with the platform for the first time :
Aat the highest position of the platformBat the mean position of the platformCfor an amplitude of gω2Dfor an amplitude of g2ω2A block of 0.5kg is placed on a horizontal platform. The system is making vertical oscillations about a fixed point with a frequency of 0.5Hz. The maximum displacement of oscillation, if the block does not lose contact with the horizontal platform is nearly
A0.5mB0.75mC1mD1.2m
An object kept on the platform a horizontal platform executing SHM, up and down with amplitude 80 cm. At what frequency will the object just lose contact with the platform?
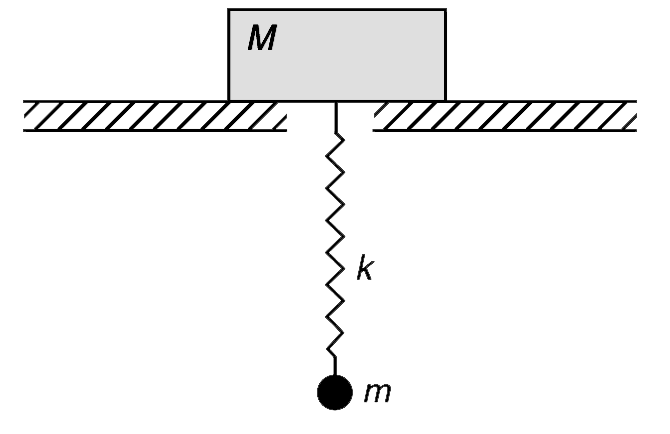
View SolutionA block of mass M is placed on top of a hole in a horizontal table. A spring of force constant k is connected to the block through the hole. The other end of the massless spring has a particle of mass m connected to it. With what maximum amplitude can the particle oscillate up and down such that the block does not lose contact with the table?
View SolutionA horizontal platform is undergoing vertical S.H>M of time period T. A block of mass M is placed on the platform . The maximum mplitude of the platform so that the block is not detached form it is
View SolutionThe average velocity of a particle executing SHM with an amplitude A and angular frequency ω during one oscillation is
View SolutionA block is kept on a rough horizontal plank. The coefficient of friction between the block and the plank is 12. The plank is undergoing SHM of angular frequency 10 rad/s. The maximum amplitude of plank in which the block does not slip over the plank is (g= 10 m/s2)
View Solution
