A block of 200 g mass is dropped from a height of 2 m on to a spring and compress the spring to a distance of 50 cm. The force constant of the spring is
20Nm−1
40Nm−1
30Nm−1
60Nm−1
The correct Answer is:B
To find the force constant of the spring when a block of mass 200 g is dropped from a height of 2 m and compresses the spring by 50 cm, we can follow these steps:
Step 1: Convert the mass to kilograms
The mass m is given as 200 g. To convert this to kilograms:
m=200 g1000=0.2 kg
Step 2: Convert the compression distance to meters
The compression of the spring x is given as 50 cm. To convert this to meters:
x=50 cm100=0.5 m
Step 3: Calculate the effective height
The effective height H from which the block falls is the sum of the height from which it is dropped and the compression of the spring:
H=2 m+0.5 m=2.5 m
Step 4: Use the conservation of energy principle
The potential energy (PE) of the block at height H is converted into the potential energy stored in the spring when it is compressed. The potential energy of the block is given by:
PE=mgh
Substituting the values:
PE=0.2 kg×10 m/s2×2.5 m=5 J
Step 5: Set the potential energy equal to the spring potential energy
The potential energy stored in the spring when compressed is given by:
PEspring=12kx2
Setting the two potential energies equal:
mgh=12kx2
Substituting the known values:
5=12k(0.5)2
Step 6: Solve for the spring constant k
Rearranging the equation to solve for k:
5=12k(0.25)
5=0.125k
k=50.125=40 N/m
Final Answer
The force constant of the spring is:
40 N/m
The mass m is given as 200 g. To convert this to kilograms:
m=200 g1000=0.2 kg
The compression of the spring x is given as 50 cm. To convert this to meters:
x=50 cm100=0.5 m
The effective height H from which the block falls is the sum of the height from which it is dropped and the compression of the spring:
H=2 m+0.5 m=2.5 m
The potential energy (PE) of the block at height H is converted into the potential energy stored in the spring when it is compressed. The potential energy of the block is given by:
PE=mgh
Substituting the values:
PE=0.2 kg×10 m/s2×2.5 m=5 J
The potential energy stored in the spring when compressed is given by:
PEspring=12kx2
Setting the two potential energies equal:
mgh=12kx2
Substituting the known values:
5=12k(0.5)2
Rearranging the equation to solve for k:
5=12k(0.25)
5=0.125k
k=50.125=40 N/m
The force constant of the spring is:
40 N/m
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MATCH THE COLUMNS
7 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - E Integer Type Questions
11 Videos
Similar Questions
A block of mass 2 kg is dropped from a height of 40 cm on a spring whose force-constant 1960Nm−1. The maximum distance through which the spring is compressed by
View SolutionA smooth block of mass m is released from rest from a height h. It slides and compresses the spring of stiffness k. Find the maximum compression of the spring .
Taking block spring a system. Now external force is doing work on system and no non-conservative force is present. The mechanincal energy should be conserved.
ΔK+ΔU=0
View Solution
Knowledge Check
A block of mass 2kg is propped from a heught of 40cm on a spring where force constant is 1960Nm−1 The maximum distance thought which the spring compressed by
A5 cmB15 cmC20 cmD10 cm
A block of mass m moving at a speed v compresses a spring through a distance x before its speed is halved. The spring constant of the spring is 6mv2nx2. Find value of n.
View SolutionA block of mass m moving at a speed 'v' compresses as spring through a distance 'x' before its speed is halved. Find the spring constant of the spring.
View SolutionA block of mass m moving at a speed v compresses a spring throgh a distance x before its speed is halved. Find the spring constant of the spring.
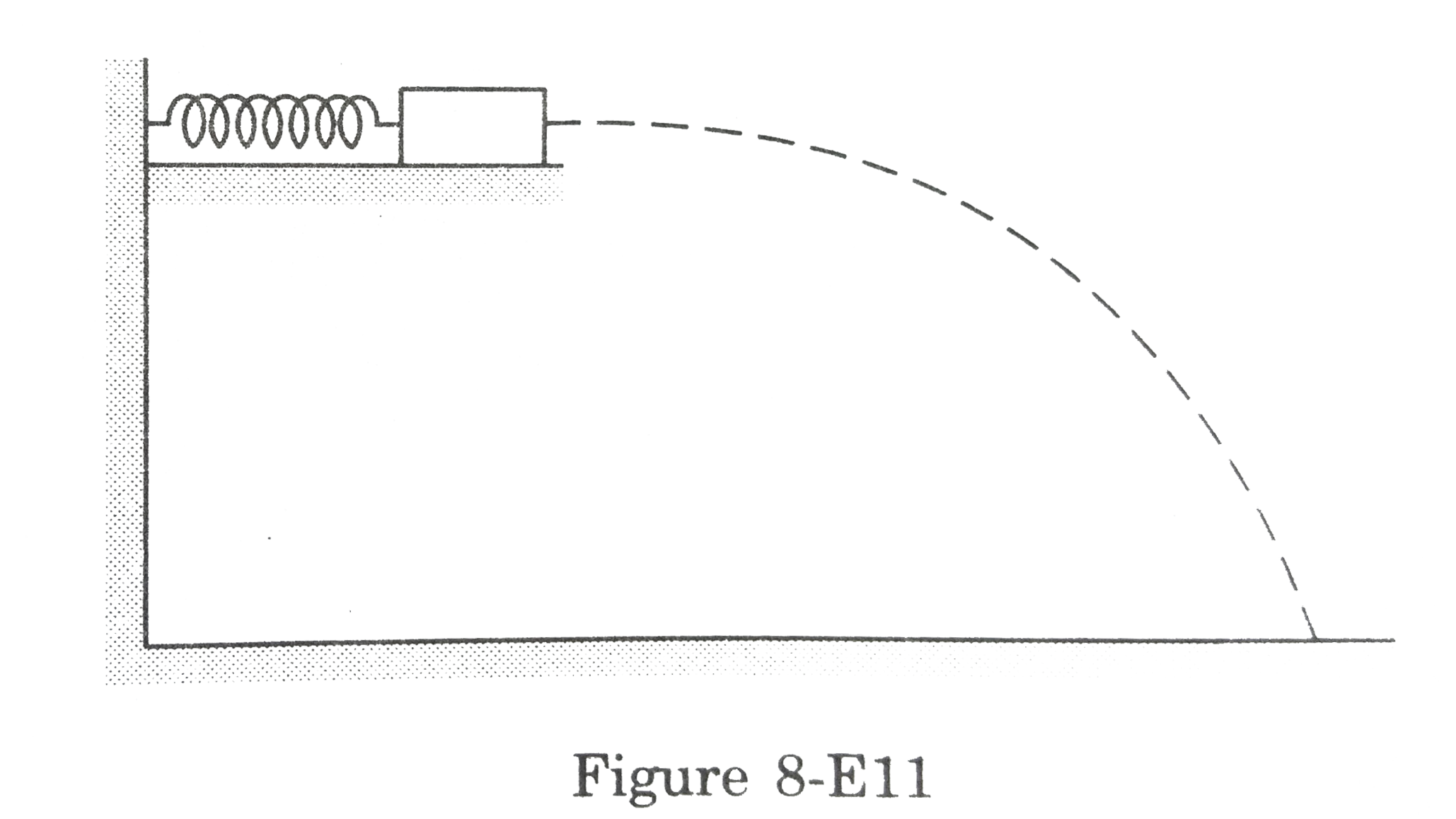
View SolutionA small block of mass 100 g is pressed again a horizontal spring fixed at one end to compress the sprign through 5.0 cm. The spring constant is 100 N/m. When released, the block moves hroizontally till it leaves the spring. Where will it hit the ground 2 m below the spring?
View SolutionA block of mass 180g is suspended by a massless spring. The spring extends by 1.8cm due to the weight of block. A particle of mass 20g is dropped from a height 80cm on the block. The collision is completely inelastic . Find the maximum elongation of the spring.
View SolutionA ball of mass m is droppped from a height h on a platform fixed at the top of a vertical spring. The platform is depressed by a distance x. What is the spring constant K?
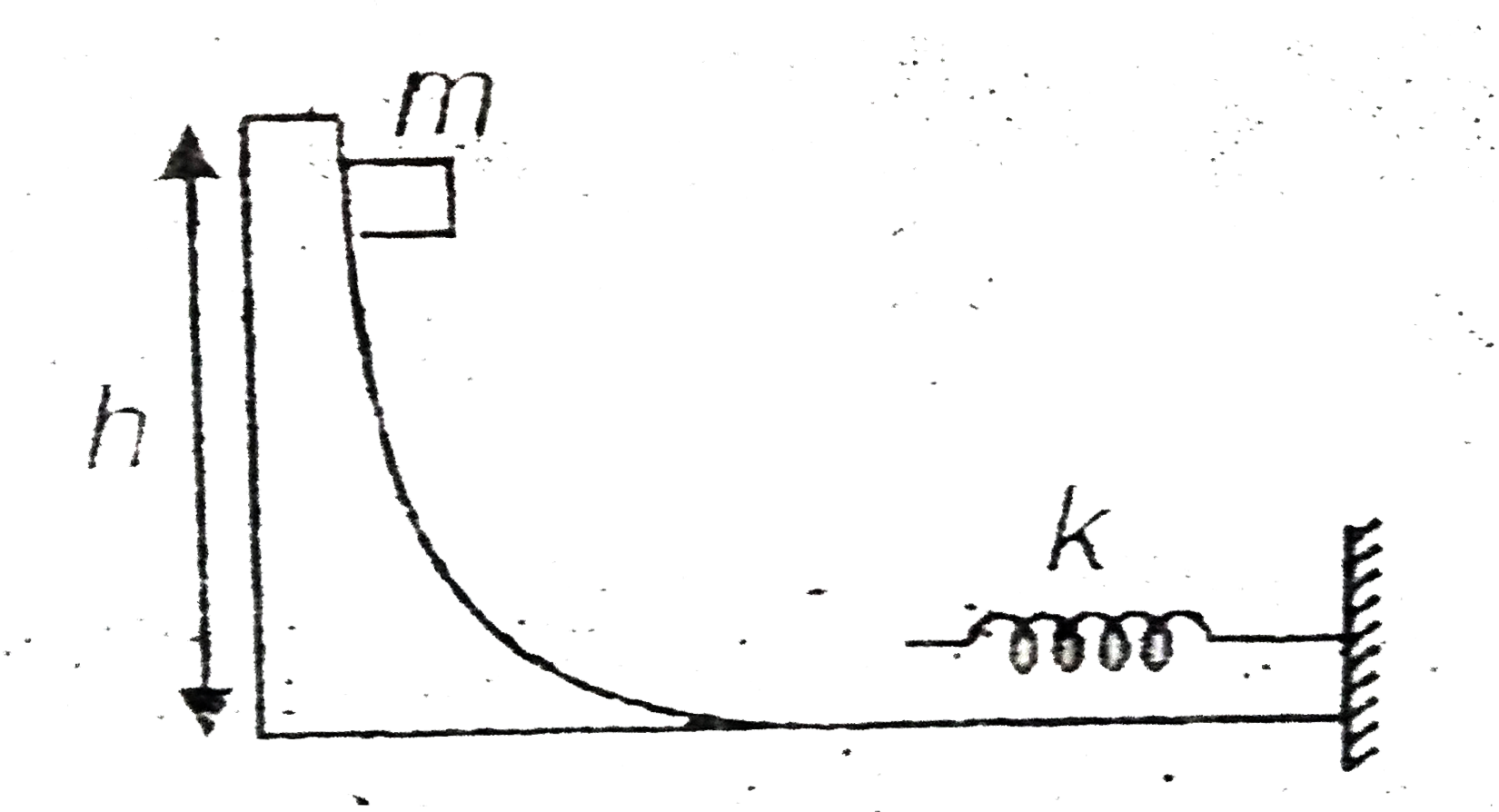
View SolutionA block of mass m is released from a height h from the top of a smooth surface. There is an ideal spring of spring constant k at the bottom of the track. Find the maximum compression in the spring (Wedge is fixed)
View Solution
