A block of mass 2.5kg is pushed 2.20m along a frictionless horizontal table by a constant force 16 N directed 45∘ above the horizontal. Determine the work done by.
(a) the applied force,
(b) the mormal force exerted by the table,
(c) the force of gravity and
(d) determine the total work done on the block.
To solve the problem step by step, we will calculate the work done by the applied force, the normal force, the force of gravity, and finally, the total work done on the block.
Given Data:
- Mass of the block, m=2.5kg
- Displacement, s=2.20m
- Applied force, F=16N
- Angle of applied force above the horizontal, θ=45∘
(a) Work Done by the Applied Force
The work done by a force is given by the formula:
W=F⋅s⋅cos(θ)
Substituting the known values:
W=16N⋅2.20m⋅cos(45∘)
Since cos(45∘)=1√2:
W=16⋅2.20⋅1√2≈16⋅2.20⋅0.7071
W≈24.9J
(b) Work Done by the Normal Force
The normal force acts perpendicular to the displacement of the block. Therefore, the work done by the normal force is:
Wnormal=Fnormal⋅s⋅cos(90∘)
Since cos(90∘)=0:
Wnormal=Fnormal⋅s⋅0=0J
(c) Work Done by the Force of Gravity
The gravitational force also acts perpendicular to the displacement. Thus, the work done by gravity is:
Wgravity=Fgravity⋅s⋅cos(90∘)
Again, since cos(90∘)=0:
Wgravity=Fgravity⋅s⋅0=0J
(d) Total Work Done on the Block
The total work done on the block is the sum of the work done by all forces:
Wtotal=Wapplied+Wnormal+Wgravity
Wtotal=24.9J+0J+0J=24.9J
Final Answers:
- (a) Work done by the applied force: 24.9J
- (b) Work done by the normal force: 0J
- (c) Work done by the force of gravity: 0J
- (d) Total work done on the block: 24.9J
- Mass of the block, m=2.5kg
- Displacement, s=2.20m
- Applied force, F=16N
- Angle of applied force above the horizontal, θ=45∘
W=F⋅s⋅cos(θ)
W=16N⋅2.20m⋅cos(45∘)
W=16⋅2.20⋅1√2≈16⋅2.20⋅0.7071
W≈24.9J
Wnormal=Fnormal⋅s⋅cos(90∘)
Wnormal=Fnormal⋅s⋅0=0J
Wgravity=Fgravity⋅s⋅cos(90∘)
Wgravity=Fgravity⋅s⋅0=0J
Wtotal=Wapplied+Wnormal+Wgravity
Wtotal=24.9J+0J+0J=24.9J
- (a) Work done by the applied force: 24.9J
- (b) Work done by the normal force: 0J
- (c) Work done by the force of gravity: 0J
- (d) Total work done on the block: 24.9J
Topper's Solved these Questions
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Exercise 9.2
9 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Exercise 9.3
2 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Miscellaneous Example
6 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question
11 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
A block of mass M is pulled along a horizontal frictionless surface by a rope of mass m. If a force P is applied at the free end of the rope, the force exerted by the rope on the block is
View SolutionA block of mass 2 kg is pulled along circular arc from position X to Y as shown in figure. The work done by the horizontal force is pulling the block from X to Y is
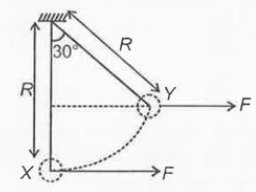
View Solution
Knowledge Check
A block of mass M is pulled along horizontal firctionless surface by a rop of mass m. Force P is applied at one end of rope. The force which the rope exerts on the block is
APM−mBPM(m+M)CPM(m+M)DPMM−m
A block of mass M is pulled along a horizontal frictionless surface by a rope of mass m . Force F is applied at one end of rope. The force which the rope exerts on the block is:
View SolutionA block of mass M is pulled along a horizontal frictionless surface by a rope of mass m as shown in A horizontal force F is applied to one end of the rope. Find
(a) the acceleration of the rope and block
(b) the force that the rope exerts on the block
(c) the tension in the rope at its mid point

View SolutionA block of mass M is pulled on a smooth horizontal table by a string making an angle θ with the horizontal as shown in figure. If the acceleration of the block is a, find the force applied by the string and by the table N on the block.

View SolutionA block of mass 20kg is placed on a rough horizontal plane and a horizontal force of 12N is applied. If coefficient of friction is 0.1 the frictional force acting on it is,
View SolutionA person pushes a block of mass 4 kg up a frictionless inclined plane 10 m long and that makes an angle of 30∘ with the horizontal . Then the work done is
View SolutionA block of mass m is slowly pulled along a curved surface from position 1 and 2. If the coefficient of kinetic friction between the block and surface is μ, find the work done by the applied force.

View SolutionThe block of mass M in figure −4.160, initially has a velocity vo to the right and its positionis much that the spring exerts no froce on it, i.e, the spring is not stretched or comkpressed. The block moves to the right a distance l before sttoping in the dotted position shown. The speing constant is k and the coefficeent of kinetic friction between block and table is μ. as the block moves the distance l, (a) what is the work done on it by the friction force ? (b) What is the work done on it by the spring force ? (c) are there other forces actionon the block, and if so what work do they do ? (d) what is the total work done on the block?
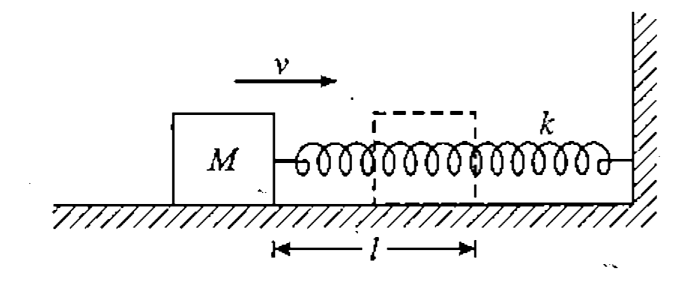
View Solution
