A block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
To find the time period of oscillations for a block of mass m hanging from a vertical spring with spring constant k, we can follow these steps:
Step 1: Understand the Forces Acting on the Block
When the block is at rest (equilibrium position), the force exerted by the spring (spring force) must balance the weight of the block. The weight of the block is given by mg, where g is the acceleration due to gravity.
Step 2: Write the Force Balance Equation
At equilibrium, the spring force Fs is equal to the weight of the block:
Fs=kΔl=mg
where Δl is the extension of the spring from its natural length.
Step 3: Solve for the Extension Δl
From the equilibrium condition, we can express the extension Δl:
Δl=mgk
Step 4: Displacement from Equilibrium
Now, when the block is displaced from its equilibrium position by a distance x, the new force balance can be considered. The total extension of the spring becomes Δl+x.
Step 5: Write the New Force Equation
The new spring force when the block is displaced is:
Fs=k(Δl+x)=k(mgk+x)=mg+kx
The net force acting on the block when it is displaced is given by:
F=mg−Fs=mg−(mg+kx)=−kx
Step 6: Apply Newton's Second Law
According to Newton's second law, the net force is equal to mass times acceleration:
ma=−kx
This can be rewritten as:
md2xdt2=−kx
Step 7: Identify the Simple Harmonic Motion
The equation d2xdt2=−kmx is the standard form of the equation for simple harmonic motion (SHM), where the angular frequency ω is given by:
ω=√km
Step 8: Find the Time Period
The time period T of the oscillation is related to the angular frequency ω by the formula:
T=2πω=2π√mk
Final Answer
Thus, the time period of oscillations for the block hanging from the spring is:
T=2π√mk
---
When the block is at rest (equilibrium position), the force exerted by the spring (spring force) must balance the weight of the block. The weight of the block is given by mg, where g is the acceleration due to gravity.
At equilibrium, the spring force Fs is equal to the weight of the block:
Fs=kΔl=mg
where Δl is the extension of the spring from its natural length.
From the equilibrium condition, we can express the extension Δl:
Δl=mgk
Now, when the block is displaced from its equilibrium position by a distance x, the new force balance can be considered. The total extension of the spring becomes Δl+x.
The new spring force when the block is displaced is:
Fs=k(Δl+x)=k(mgk+x)=mg+kx
The net force acting on the block when it is displaced is given by:
F=mg−Fs=mg−(mg+kx)=−kx
According to Newton's second law, the net force is equal to mass times acceleration:
ma=−kx
This can be rewritten as:
md2xdt2=−kx
The equation d2xdt2=−kmx is the standard form of the equation for simple harmonic motion (SHM), where the angular frequency ω is given by:
ω=√km
The time period T of the oscillation is related to the angular frequency ω by the formula:
T=2πω=2π√mk
Thus, the time period of oscillations for the block hanging from the spring is:
T=2π√mk
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Short Answer
13 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective 1
21 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises
58 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Exercises
32 Videos
Similar Questions
A block of mass m is connected with two ideal pullies and a massless spring of spring constant K as shown in figure. The block is slightly displaced from its equilibrium position. If the time period of oscillation is μπ√mK. Then find the value of μ.

View SolutionA block of mass m is connected with two ideal pullies and a massless spring of spring constant K as shown in figure. The block is slightly displaced from its equilibrium position. If the time period of oscillation is μπ√mK. Then find the value of μ.

View Solution
Knowledge Check
A block of mass m hangs from three springs having same spring constant k. If the mass is slightly displaced downwards, the time period of oscillation will be
 A2π√m3kB2π√3m2kC2π√2m3kD2π√3km
A2π√m3kB2π√3m2kC2π√2m3kD2π√3kmA block of mass m length force a verical of spring constant k If the block is polled down by a distance of 2mg/k from its equilibrium position and released for the subsequent in the spring to maximum compressed in it mg/k
A2B3C4D1A load of mass M is attached to the bottom of a spring of mass 'M/3' and spring constant 'K'. If the system is set into oscillation, the time period of oscillation is
A2π3√10MKB4π√M3KC4π√MKD2π√M3K
A block of mass m suspended from a spring of spring constant k. Find the amplitude of S.H.M.
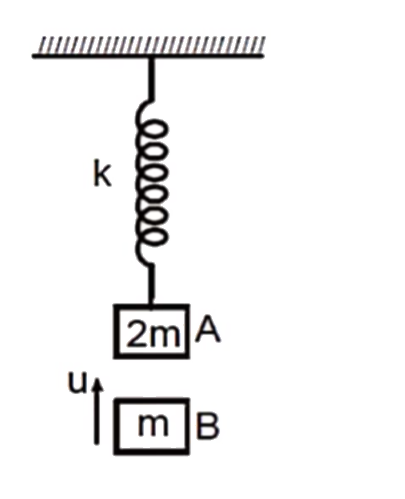
View SolutionA block A of mass 2m is hanging from a vertical massless spring of spring constant k and is in equilibrium. Another block B of mass m strikes the block A with velocity u and sticks to it as shown in the figure. The magnitude of the acceleration of the combined system of the blocks just after the collision is
View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10cm, then the period of oscillation is

View SolutionA system shown in the figure consists of a massless pulley, a spring of force constant k displaced vertically downwards from its equilibrium position and released, then the Period of vertical oscillations is

View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shwon in figure . Show that when the mass is displaced from its equilibrium position on either side, it executes a simple harmonic motion. Find th eperiod of oscillation.

View Solution
