A block of mass m is attached to two unstretched springs of spring constants k1andk2 as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as it psses through the mean position shown.

The correct Answer is:A, B
The body is displayed x towards righ.
Let the velocity of the body be v at its mean position.
Applying law of conservation of energy
12mv2=12k1x2+12k2x2

→mv2=x2(k1+k2)
→v2=(x2k1+k2m
→v=x√k1+k2m
Topper's Solved these Questions
Similar Questions
A block of mass m is attached to two unstretched springs of spring constant k1 and k2 as shown in figure. The block is displaced towards right through a distance 'x' and is released. Find the speed of the block as it passes through a distance x/4 from its mean position. All the surfaces are smooth.
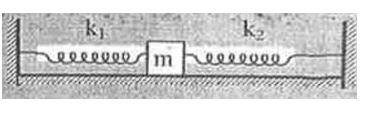
View SolutionA block of mass m = 2 kg is attached to two unstretched spring of force constant k1=100N/m and k2=125N/m
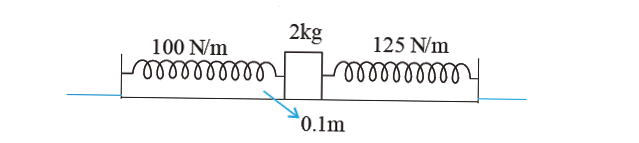
The block is displaced towards left through a distance of 10 cm and released. Find the speed of the block as it passes through the mean position.
View Solution
Knowledge Check
A block of mass m is attached to two unstretched springs of spring constants k1andk2 as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as it psses through the mean position shown.
 A√k1+k2mxB√k1k2m(k1+k2)xC ⎷k21k22m(k21+k22)xD ⎷k31k32m(k31+k32)
A√k1+k2mxB√k1k2m(k1+k2)xC ⎷k21k22m(k21+k22)xD ⎷k31k32m(k31+k32)
A block of mass m is attached to two unstretched springs of spring constant k, each as shown. The block is displaced towards right through a distance x and is released The speed of the block as it passes through the mean position will beAx√m2kBx√2kmCxmkDx2kmA block of mass m is attached to four unstretched massless springs of spring constant k1andk2 as shown in figure. The block is displaced towards right through distance x and is released. Speed of block when displacement of block is x/2 from mean position is :
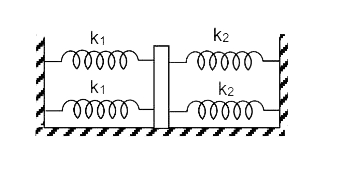 A√2(k1+k2)xmB√3(k1+k2)x22mC√(k1k2)3(k1+k2)mD√(k1+k2)x(k1+k2)m
A√2(k1+k2)xmB√3(k1+k2)x22mC√(k1k2)3(k1+k2)mD√(k1+k2)x(k1+k2)m
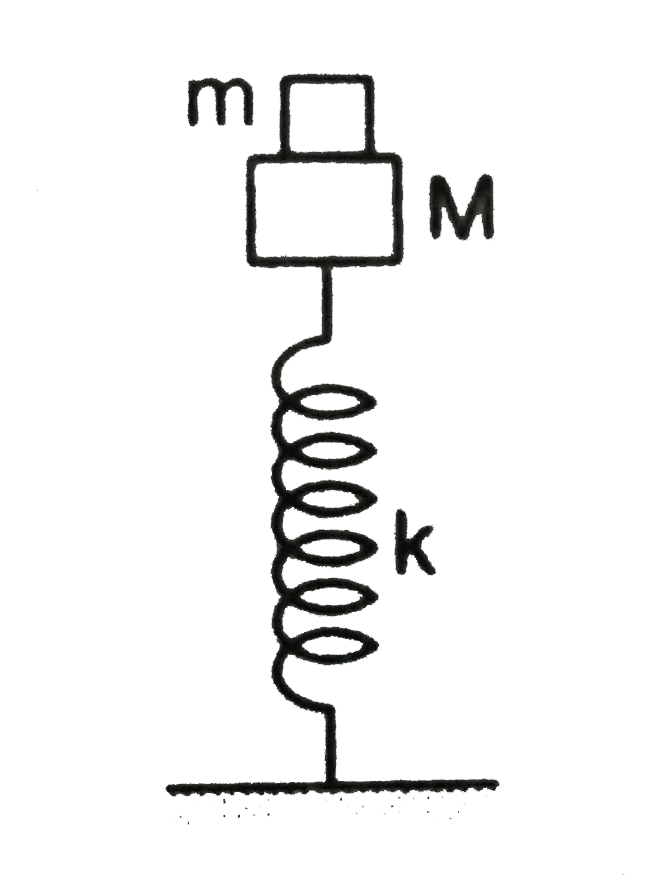
A small block of mass m is kept on a bigger block of mass M which is attached to a vertical spring of spring constant k as shown in the figure. The system oscilates verticaly. a.Find the resultant force on the smaller block when it is displaced through a distance x above its equilibrium position. b. find the normal force on the smaller blok at this position. When is this force smallest smaller block at this position. When is this force smallest in magnitude? c. What can be the maximum amplitude with which the two blocks may oscillate together?
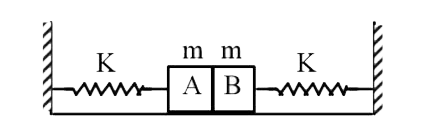
View SolutionTwo blocks each of mass m are connected with springs each of force constant K as shown in fig. The mass A is displaced to the left & B to the right by the same amount and released then the time period of oscillation is -
View SolutionA block of mass m is connected between two springs (constants K1 and K2) as shown in the figure and is made to oscillate, the frequency of oscillation of the system shall be-

View SolutionA block of mass m is suspended by different springs of force constant shown in figure.

View SolutionA 2 kg block is connected with two springs of force constants k1=100N/m and k2=300N/m as shown in figure. The block is released from rest with the springs unstretched. The acceleration of the block in its lowest postion is (g=10m/s2)

View Solution
