Question

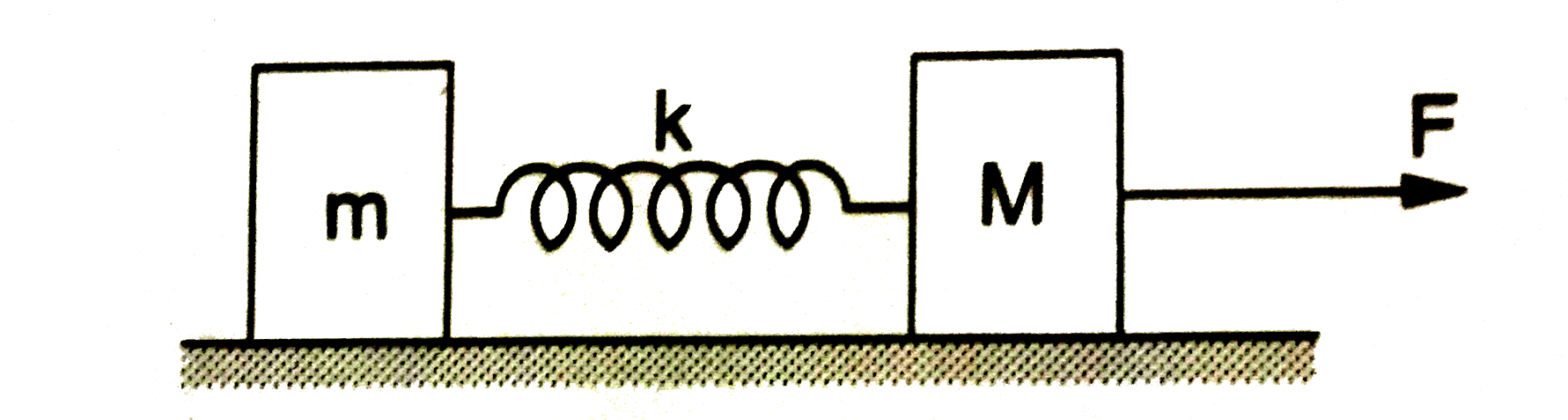
A block of mass m is connect to another block of mass M by a massless spring of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unsrtretched when a constnt force F starts acting on the block of mass M to pull it. Find the maximum extension of the spring.

Explanation

Let us take the two blocks plus the spring as the system. The centre of mass of the system moves with an acceleration `a=F/(m+M)`. Let us work from a reference frame with its origin at the centre of mass. As this frame is accelerated with respect to the ground we have to apply pseudo force ma towards dlet on tbe block of mass m an Ma towards left on theblock of mass M. The net exterN/Al force on m is
`F_1=ma=(mF)/(m+M)` towrds left
and the net exterN/Al force on M is
`F_2=F-Ma=F-(MF)/(m+M)=(mF)/(m+M)` towards right.
The situation from this frame ils shown in ure. As the centre of mass is at rest in this frame, the blcoks move in opposite directions and come to instantaneous rest at some instant. The extension of the spring will be maximum at this instasnt. Suppose the left block through a distance `x_2` from the initial positions.
The total work done by the exterN/Al forces `F_1 and F_2` in this period are
`W=F_1x_1+F_2x_2=(mF)/(m+M)(x_1+x_2)`
This should be equal to the increase in the potential energy of the spring as there is no change in the kinetic energy. Thus,
`(mF)/(m+M)(x_1+x_2)=1/2k(x_1+x_2)^2`
or, `x_1+x_2=(2mF)/(k(m+M))`
This is the maximum extension of the spring.