A block of mass m is projected up with a velocity $v_{0}$ along an inclined plane of angle of inclination $θ = 37^{\circ}$ . The coefficient of friction between the inclined plane AB and blocks is $μ (= tan θ)$ . Find the values of $v_{0}$ so that the block moves in a circular path from B to C.

Text Solution

Verified by Experts

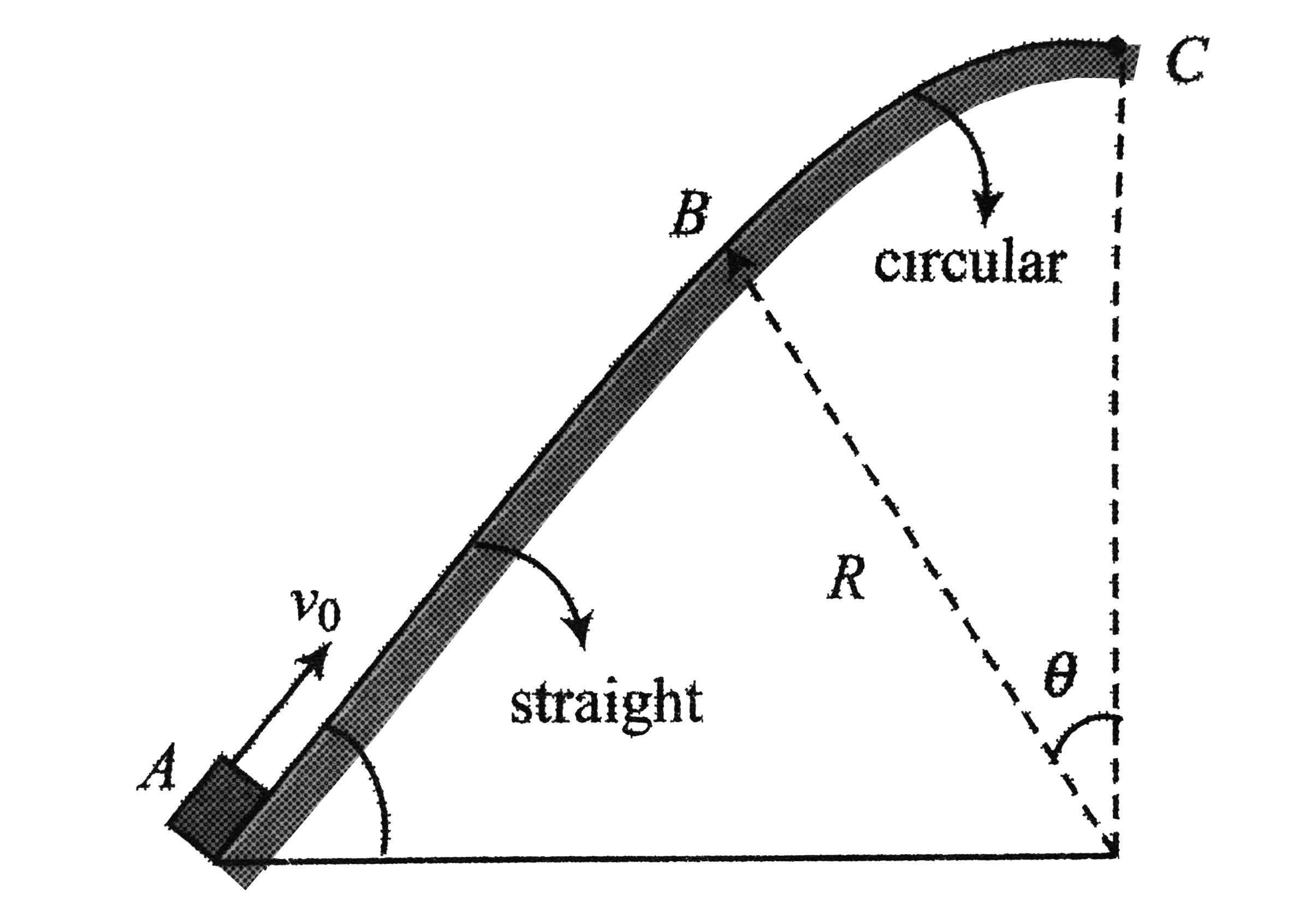
In traingle ABO, $\frac{R}{l} = tan θ \Rightarrow l = \frac{4 R}{3}$

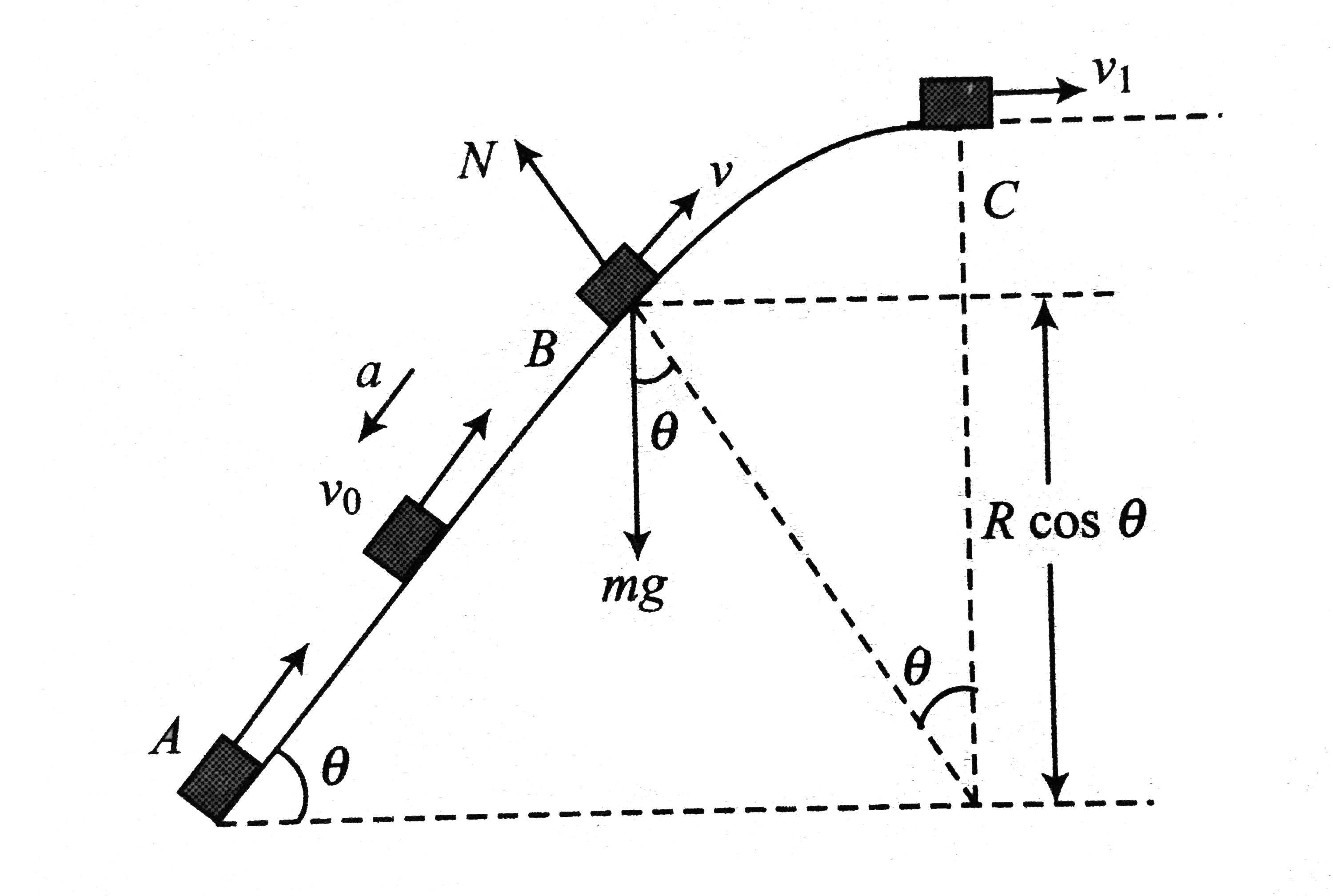
For contact not to be lost at B:
$m g cos θ - N = \frac{m v^{2}}{R}$
$\Rightarrow N = m g cos θ - \frac{m v^{2}}{R} = \geq 0$
$\Rightarrow v \leq \sqrt{g R cos θ}$ (i)
From B to C: $Δ K + Δ U = 0$
$(\frac{1}{2} m v_{1}^{2} - \frac{1}{2} m v^{2}) + m g (R - R cos θ) = 0$
$\Rightarrow v_{2} = v_{1}^{2} + 2 g R (1 - cos θ)$ (ii)
From A to B: $a = g sin θ + μ g cos θ$
$= g sin θ + (tan θ) g cos θ$
$\Rightarrow a = 2 g sin θ$
$\Rightarrow v_{2} = v_{0}^{2} - 2 a l$
$\Rightarrow v^{2} = v_{0}^{2} - \frac{4 g sin θ R}{tan θ}$
$\Rightarrow v^{2} = v_{0}^{2} - 4 g R cos θ$ (iii)
From Eqs (i) and (iii),
$v_{0}^{2} - 4 g R cos θ \leq g R cos θ$ or $v_{0}^{2} \leq 5 g R cos θ$
$\Rightarrow v_{0}^{2} \leq 5 g R (\frac{4}{5}) = 4 g R \Rightarrow v_{0} \leq \sqrt{4 g R}$ (iv)
From Eqs (ii) and (iii),
$v_{1}^{2} + 2 g R [1 - cos θ] = v_{0}^{2} - 4 g R cos θ$
$\Rightarrow v_{1}^{2} = v_{0}^{2} - 2 g R - 2 g R cos θ$
Now to reach at $C : V_{1} \geq 0$
or $v_{0}^{2} - 2 g R - 2 g R cos θ \geq 0$
$\Rightarrow v_{0} \geq \sqrt{2 g R [1 + cos θ]}$
$\Rightarrow v_{0} \geq \sqrt{2 g R [1 + 4 / 5]} \Rightarrow v_{0} \geq \sqrt{\frac{18 g R}{5}}$ (v)
From (iv) and (v) $\sqrt{\frac{18 g R}{5}} \leq v_{0} \leq \sqrt{4 g R}$

A body is projected up along a rough inclined plane of inclination $45^{\circ}$ . The coefficient of friction is 0.5. Then the retardation of the block is
A $\frac{g}{2 \sqrt{2}}$
B $\frac{g}{2}$
C $\frac{3 g}{2 \sqrt{2}}$
D $\frac{g}{\sqrt{2}}$
A block of mass m slides down an inclined plane of inclination $θ$ with uniform speed. The coefficient of friction between the block and the plane is $μ$ . The contact force between the block and the plane is
Amg
B $m g sin θ \sqrt{1 + μ^{2}}$
C $m g sin θ$
D $\sqrt{{(m g sin θ)}^{2} + {(μ m g cos θ)}^{2}}$