A block of mass m is pulled slowly by a minimum constant force on a rough (μ) horizontal surface through a distance x. Find work done by force F.
To solve the problem of finding the work done by a constant force F pulling a block of mass m on a rough horizontal surface with a coefficient of friction μ through a distance x, we can follow these steps:
Step 1: Identify the Forces Acting on the Block
- The forces acting on the block include:
- The gravitational force mg acting downward.
- The normal force N acting upward.
- The applied force F acting at an angle θ to the horizontal.
- The frictional force f acting opposite to the direction of motion.
Step 2: Write the Equation for the Normal Force
- The normal force can be expressed as:
N=mg−Fsinθ
This equation accounts for the vertical forces acting on the block.
Step 3: Write the Equation for the Horizontal Forces
- In the horizontal direction, the net force must be zero since the block is moving at constant velocity (pulled slowly):
Fcosθ−f=0
where f=μN. Substituting for N:
f=μ(mg−Fsinθ)
Thus, we can rewrite the horizontal force equation:
Fcosθ−μ(mg−Fsinθ)=0
Step 4: Solve for the Applied Force F
- Rearranging the equation gives:
Fcosθ=μmg−μFsinθ
F(cosθ+μsinθ)=μmg
Therefore, the minimum force F required to move the block is:
F=μmgcosθ+μsinθ
Step 5: Calculate the Work Done by the Force
- The work done W by the force F while moving the block through distance x is given by:
W=F⋅x⋅cosθ
Substituting for F:
W=(μmgcosθ+μsinθ)x⋅cosθ
Step 6: Simplify the Expression
- The expression simplifies to:
W=μmg⋅x⋅cosθcosθ+μsinθ
Step 7: Substitute for cosθ
- From the geometry of the situation, we can express cosθ in terms of μ:
cosθ=1√1+μ2
- Substitute this into the work done equation:
W=μmg⋅x⋅1√1+μ21√1+μ2+μ⋅μ√1+μ2
Step 8: Final Expression for Work Done
- After simplification, we find:
W=μmg⋅x√1+μ2
Final Answer
The work done by the force F is:
W=μmg⋅x√1+μ2
- The forces acting on the block include:
- The gravitational force mg acting downward.
- The normal force N acting upward.
- The applied force F acting at an angle θ to the horizontal.
- The frictional force f acting opposite to the direction of motion.
- The normal force can be expressed as:
N=mg−Fsinθ
This equation accounts for the vertical forces acting on the block.
- In the horizontal direction, the net force must be zero since the block is moving at constant velocity (pulled slowly):
Fcosθ−f=0
where f=μN. Substituting for N:
f=μ(mg−Fsinθ)
Thus, we can rewrite the horizontal force equation:
Fcosθ−μ(mg−Fsinθ)=0
- Rearranging the equation gives:
Fcosθ=μmg−μFsinθ
F(cosθ+μsinθ)=μmg
Therefore, the minimum force F required to move the block is:
F=μmgcosθ+μsinθ
- The work done W by the force F while moving the block through distance x is given by:
W=F⋅x⋅cosθ
Substituting for F:
W=(μmgcosθ+μsinθ)x⋅cosθ
- The expression simplifies to:
W=μmg⋅x⋅cosθcosθ+μsinθ
- From the geometry of the situation, we can express cosθ in terms of μ:
cosθ=1√1+μ2
- Substitute this into the work done equation:
W=μmg⋅x⋅1√1+μ21√1+μ2+μ⋅μ√1+μ2
- After simplification, we find:
W=μmg⋅x√1+μ2
The work done by the force F is:
W=μmg⋅x√1+μ2
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.2
25 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.3
26 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Solved Examples
15 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
A block of mass m is pulled by a force of constant power P placed on a rough horizontal plane. The friction coefficient between the block and the surface is μ. Then
View SolutionA block of mass m is pulled by a constant powert P placed on a rough horizontal plane. The friction coefficient the block and surface is μ. The maximum velocity of the block is.
View SolutionA block of mass m=2kg is pulled by a force F=40N upwards through a height h=2m. Find the work done on the block by the applied force F and its weight mg. (g=10m/s2).

View SolutionA block of mass m=2kg is pulled by a force F=40N upwards through a height h=2m. Find the work done on the block by the applied force F and its weight mg. (g=10m/s2).

View Solution
A block of mass 1 kg is pulled slowly along the curve path ACB by a tangential force as shown in figure. The magnitude of work done by the frictional force when the block moves from A to B is
View SolutionA block of 10kg is pulled at a constant speed on a rough horizontal plane by a force of 20N. Calculate the coefficient of friction ?
View SolutionBlock A of mass 1kg is placed on the rough surface of block B of mass 3kg. Block B is placed on smooth horizontal surface. Blocks are given the velocities as shown. Find net work done by the frictional force. [in (−)veJ].
 .
.
View Solutiona block of mass 0.1 kg attached to a spring of spring constant400Nm pulled horizontally from x=0 tox1=10mm. Find the work done by the spring force
View SolutionA block of mass M is pulled along a horizontal frictionless surface by a rope of mass m as shown in A horizontal force F is applied to one end of the rope. Find
(a) the acceleration of the rope and block
(b) the force that the rope exerts on the block
(c) the tension in the rope at its mid point

View SolutionA bob of mass m is pulled along a circular arc by means of a constant horizontal force P as shown. Work done in lifting the bob from A to B is
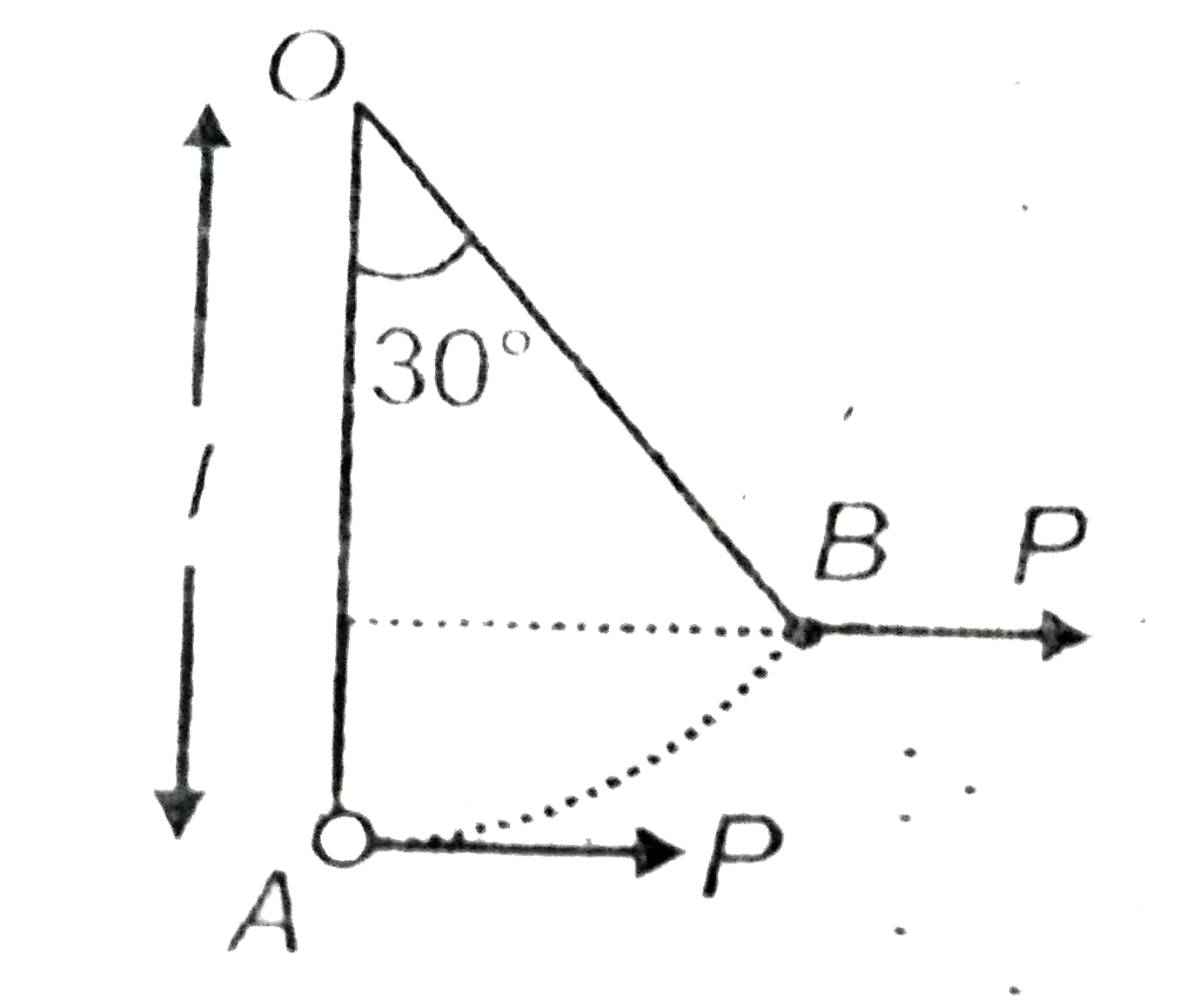
View Solution
