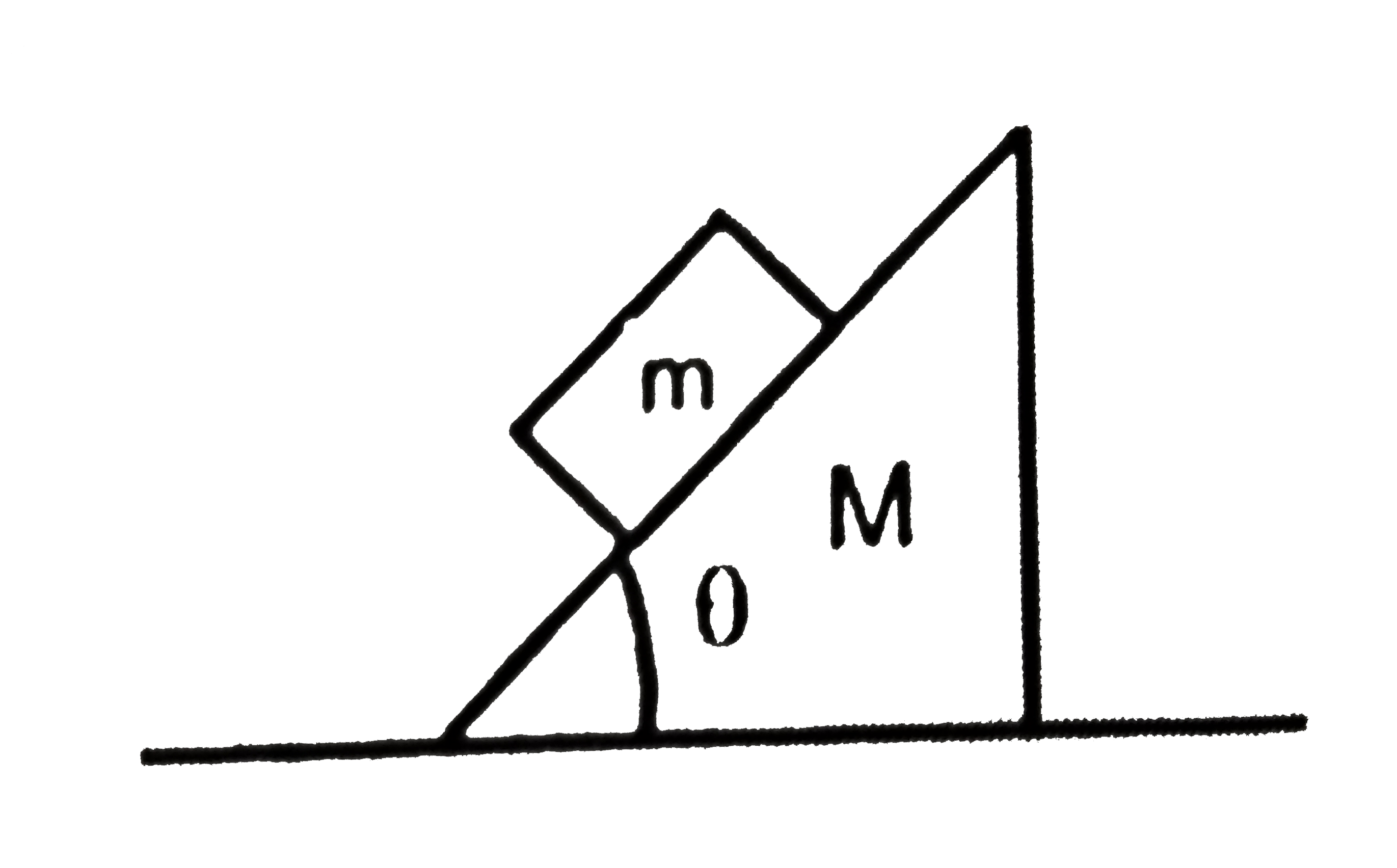
A block of mass m slides down on inclined wedge of same mass m as shown in figure . Friction is absent everywhere . Acceleration of centre of mass of the block and wedge is
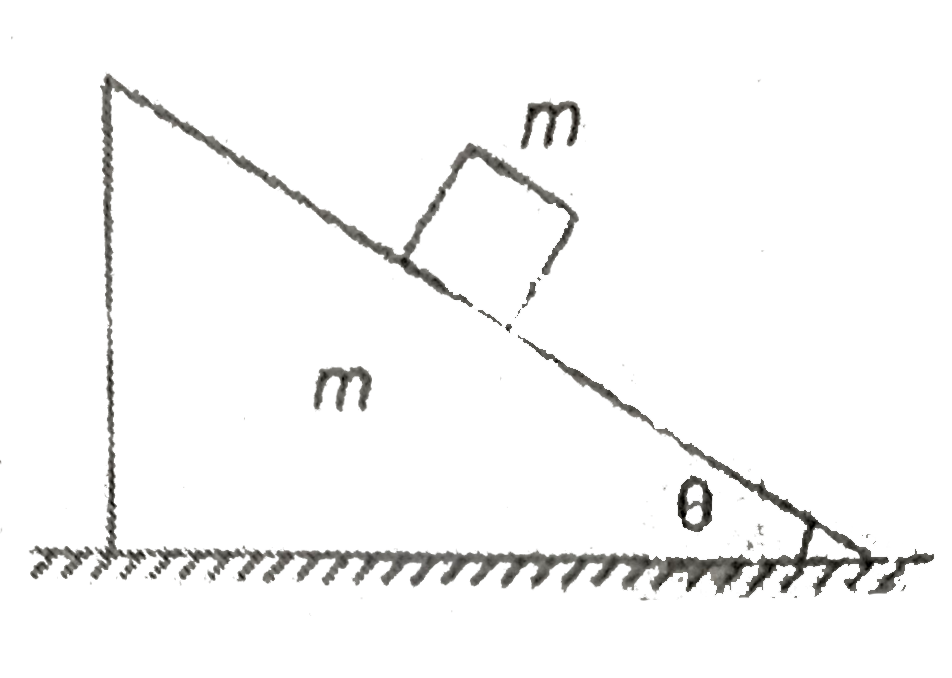
zero
gsin2θ(1+sin2θ)
gcos2θ(1+sin2θ)
gsinθ(1+cosθ)
Step by step video & image solution for A block of mass m slides down on inclined wedge of same mass m as shown in figure . Friction is absent everywhere . Acceleration of centre of mass of the block and wedge is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - More a than one option is Correct
1 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CENTRE OF MASSBOOK - DC PANDEYCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery
27 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
Similar Questions
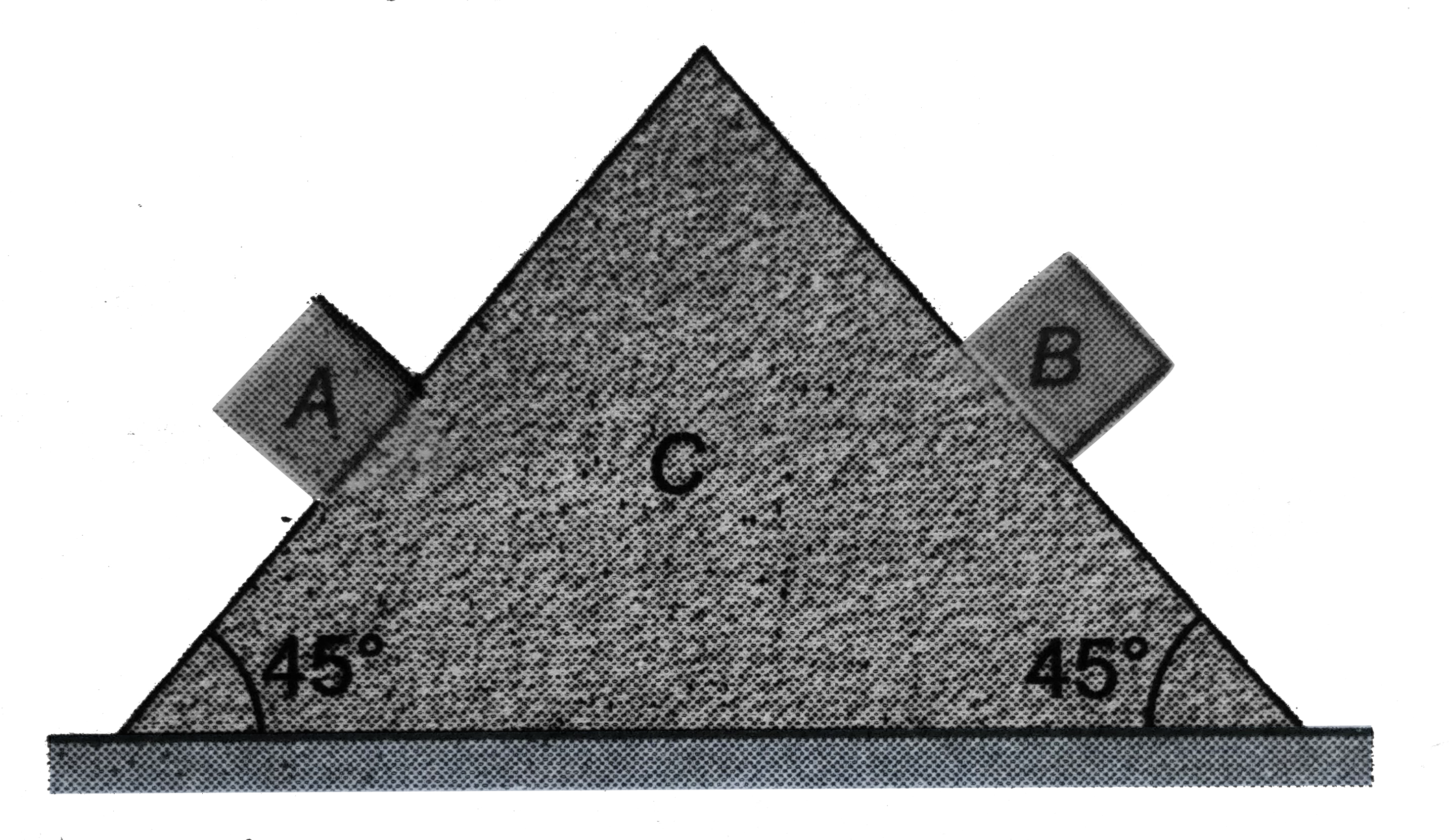
Two blocks A and B of equal masses are released on two sides of a fixed wedge C as shown in figure. Find the acceleration of centre of mass of blocks A and B. Neglect friction.
View SolutionA block of mass m is released from a wedge of mass m as shown in figure . Find the time taken by the block to reach the end of the wedge.
View Solution
Knowledge Check
A block of mass m slides down on a wedge of mass M as shown in figure .Let a1 be the asseleration of the acceleration of and a2 the the acceleration od block 1N1 is the normal reaction between block and wedge and N2 the normal reaction between wedge and gound .frication is absent everwhere .Select the correct alternative(s)
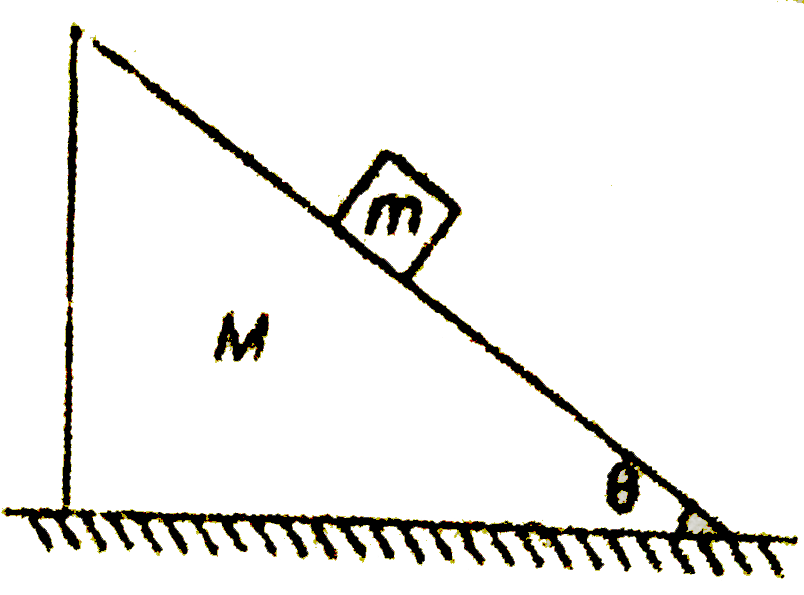 AN2<(M+m)gBN2<M(gcosθ−|a1|sinθ)CN1sinθ=M|a1|Dma2=−Ma1
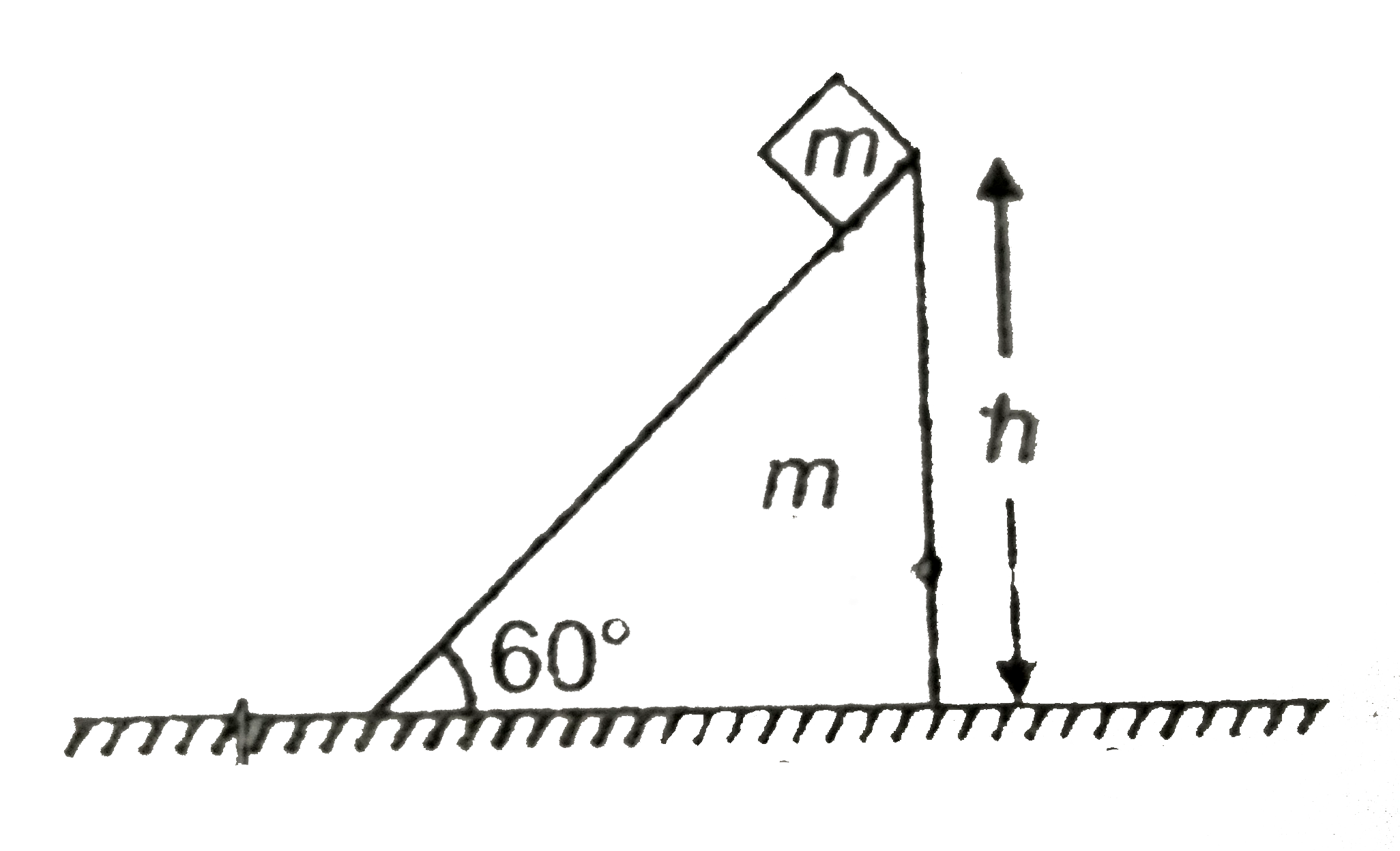
AN2<(M+m)gBN2<M(gcosθ−|a1|sinθ)CN1sinθ=M|a1|Dma2=−Ma1A block of mass m slides down a wedge of mass M as shown . The whole system is at rest , when the height of the block is h above the ground. The wedge surface is smooth and gradually flattens. There is no friction between wedge and ground.
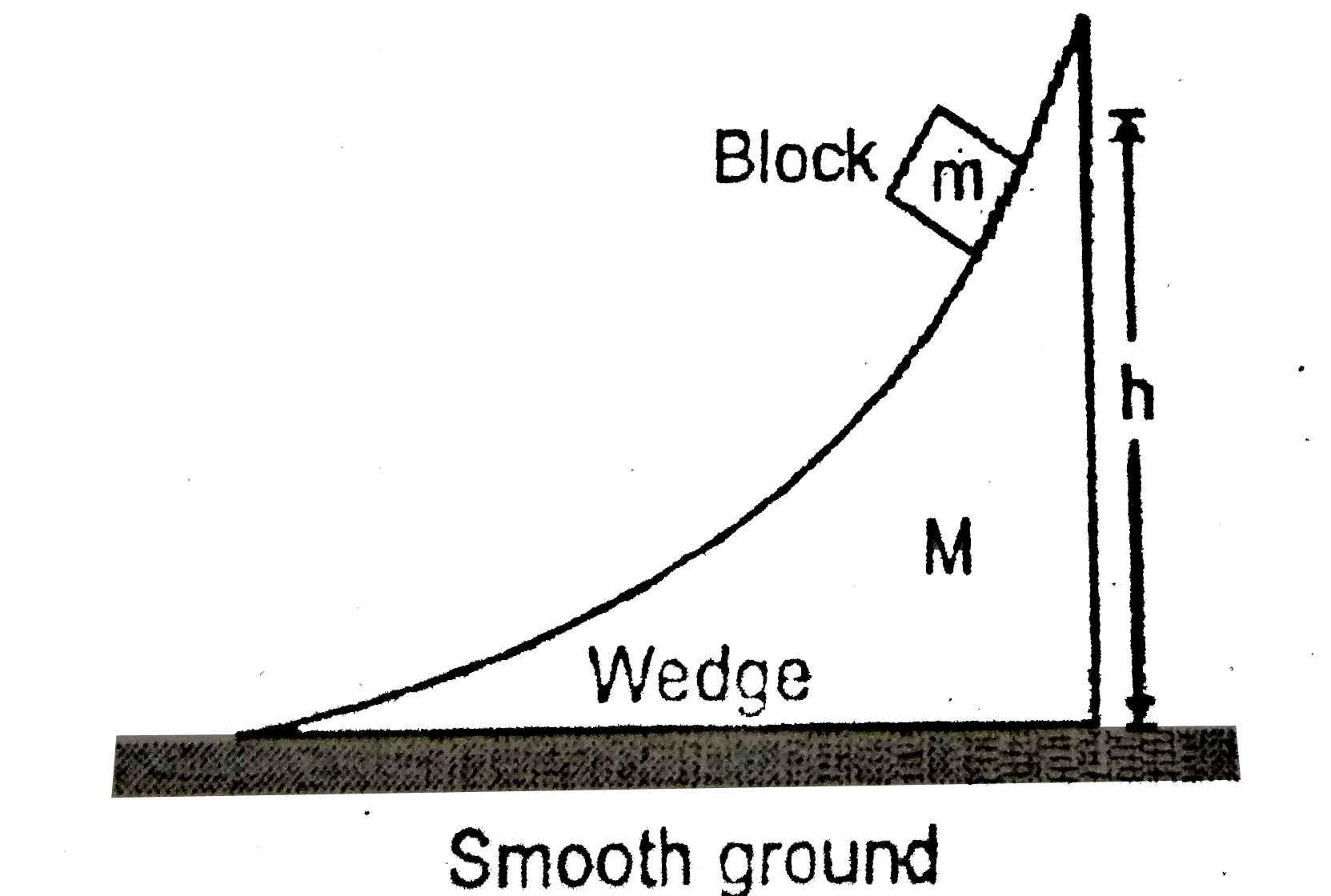
If there is no friction any where, the speed of the wedge, as the block leaves the wedge is :Am√2gh(M+m)MBM√2gh(M+m)mC(√2gh)mM+mD(√2gh)MM+mA block of mass m slides down a wedge of mass M as shown . The whole system is at rest , when the height of the block is h above the ground. The wedge surface is smooth and gradually flattens. There is no friction between wedge and ground.
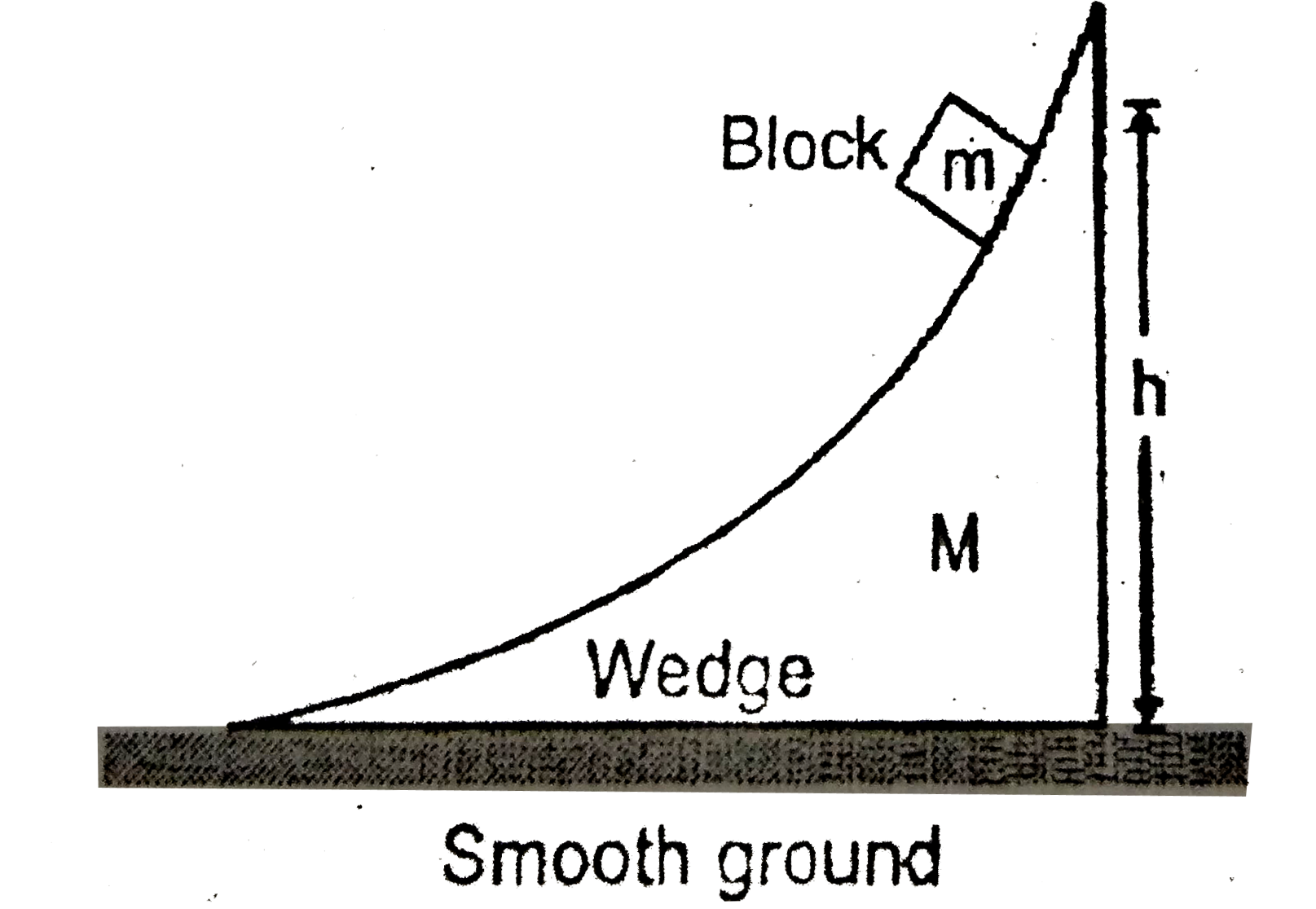
If there would have been friction wedge and block , which of the following quantities would still remains conserved ?ALinear momentum of the system along horizontal directionBLinear momentum of the system along vertical directionCLinear momentum of the system along a tangent to the curved surface of the wedgeDMechanical energy of the system
A cubical block of mass m is sliding on an inclined right angle trough as shown in the figure. If coefficient of friction is μ , find the acceleration of the block.
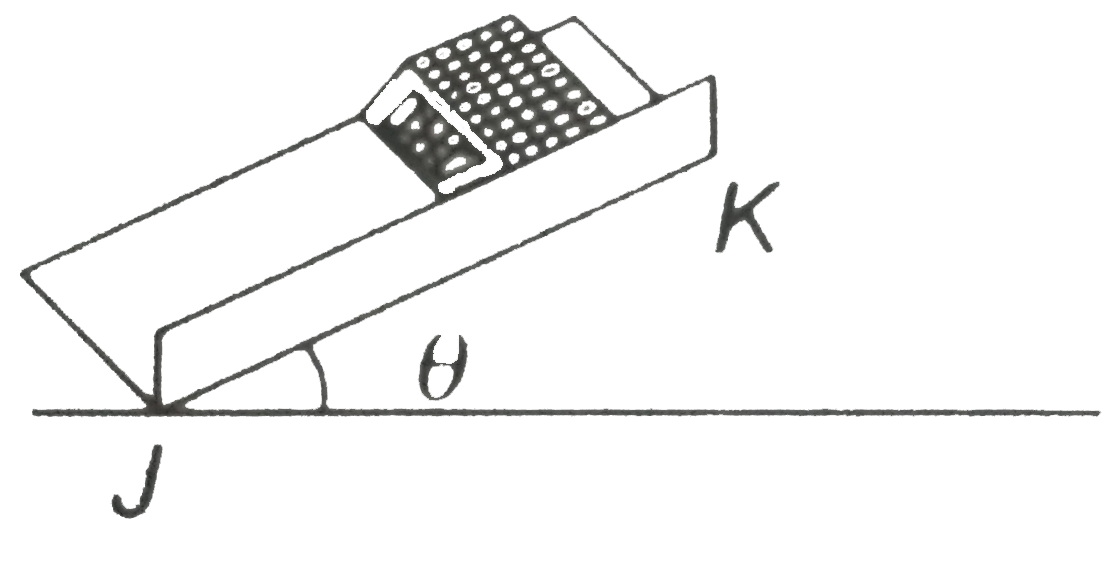
View SolutionA block of mass m is placed on the inclined sufrace of a wedge as shown in fig. Calculate the acceleration of the wedge and the block when the block is released. Assume all surfaces are frictionless.

View SolutionA block of mass m lies on wedge of mass Mas shown in figure. Find the minimum friction coeffcient required between wedge Mand ground so that it does not move while block m slips down on it.
View SolutionA block of mass m slides down a wedge of mass M as shown . The whole system is at rest , when the height of the block is h above the ground. The wedge surface is smooth and gradually flattens. There is no friction between wedge and ground.
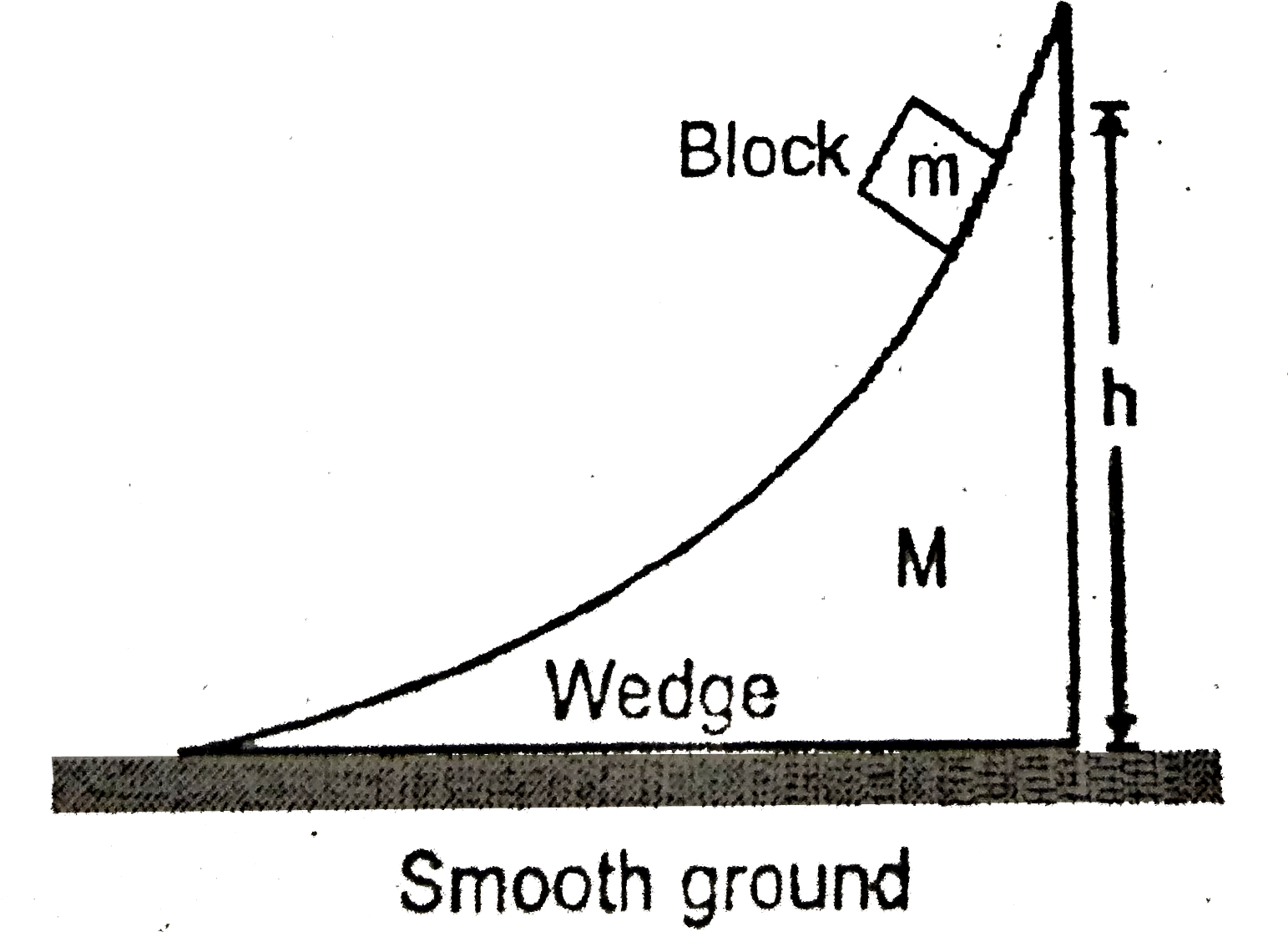
As the block slides down, which of the following quantities associated with the system remains conserved ?
View SolutionA block of mass m is placed on a smooth inclined wedge ABC of inclination theta as shown in the figure. The wedge is given an acceleration a towards the right. The relation between a and theta for the block to remain stationary on the wedge is.

View Solution
