Two particles A and B of equal mass m are attached by a string of length 2l and initially placed over a smooth horizontal table in the positoin shown in fig. particle B is projected across the table with speed u perpendicular to AB as shown in the figure. find the velocities of each particle after the string becomes taut and the magnitude of the impulse tension.
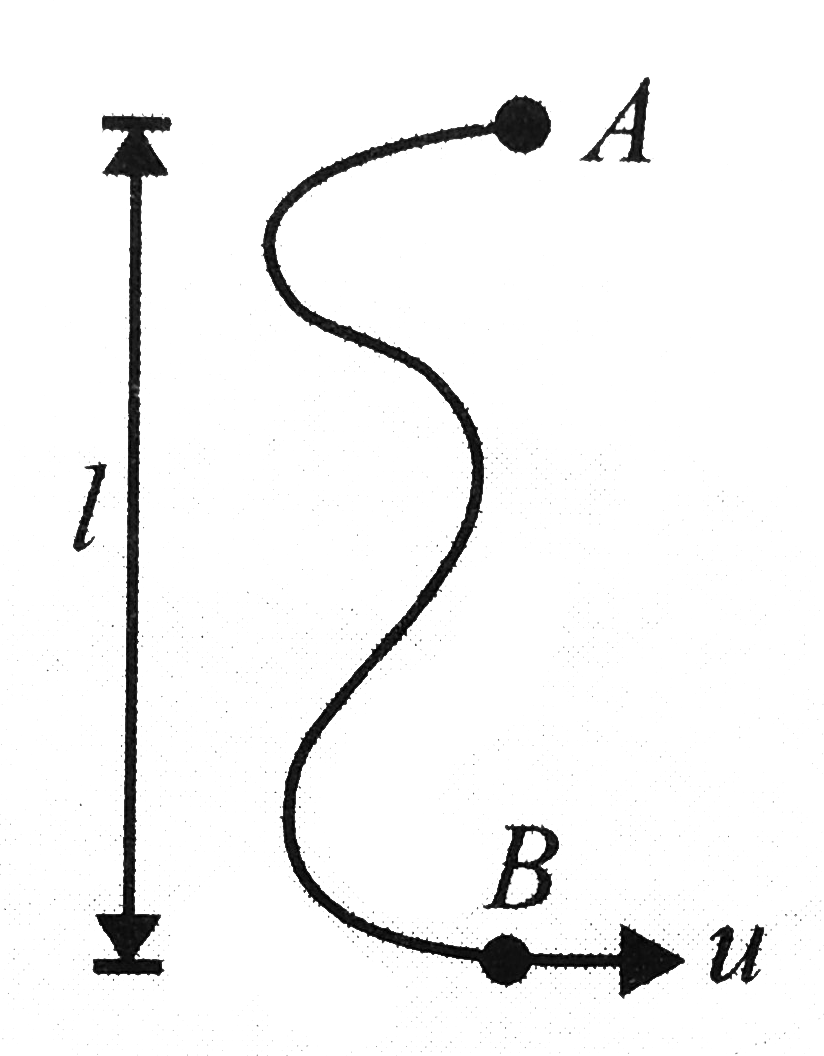
u√34
u√3
u√32
u2
Step by step video & image solution for Two particles A and B of equal mass m are attached by a string of length 2l and initially placed over a smooth horizontal table in the positoin shown in fig. particle B is projected across the table with speed u perpendicular to AB as shown in the figure. find the velocities of each particle after the string becomes taut and the magnitude of the impulse tension. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - More a than one option is Correct
1 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CENTRE OF MASSBOOK - DC PANDEYCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery
27 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
Similar Questions
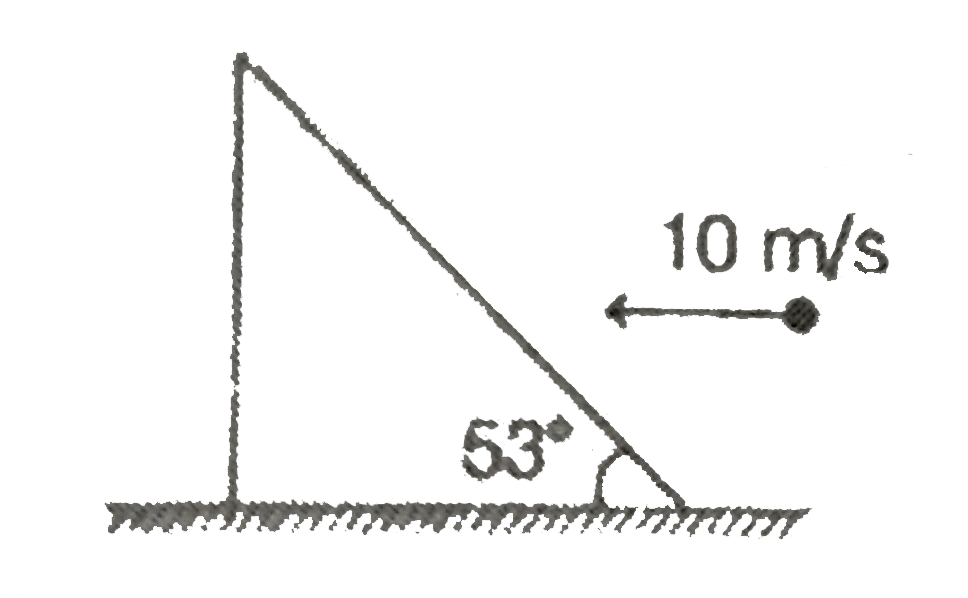
A ball mass 2 kg moving horizontally with velocity 10 m/s hits a wedge of mass 5 kg placed on a horizontal surface as shown in the figure. Just after collision klvelocity of wedge is 3.2 m/s. There is no friction at any contact surface. Then (take sin 30∘=3/5)
View SolutionComprehension # 1
If net force on a system in a particular direction is zero (say in horizontal direction), we can apply: ΣmRxR=ΣmLxL,ΣmRvR=ΣmLvL and ΣmRaR=ΣmLaL
Here R stands for the masses which are moving towards right and L for the masses towards left, x is displacement, v is velocity and a the acceleration (all with respect to ground).
A small block of mass m=1kg is placed over a wedge of mass M=4kg as shown in figure. Mass m is released from rest. All surface are smooth. Origin O is as shown.

Final velocity of the wedge is ..........m/s :-
View SolutionComprehension # 1
If net force on a system in a particular direction is zero (say in horizontal direction), we can apply: ΣmRxR=ΣmLxL,ΣmRvR=ΣmLvL and ΣmRaR=ΣmLaL
Here R stands for the masses which are moving towards right and L for the masses towards left, x is displacement, v is velocity and a the acceleration (all with respect to ground).
A small block of mass m=1kg is placed over a wedge of mass M=4kg as shown in figure. Mass m is released from rest. All surface are smooth. Origin O is as shown.

Final velocity of the wedge is ..........m/s :-
View SolutionA rod of weight w is supported by two parallel knife edges A and B and is in equilibrium in a horizontal position. The knives are at a distance d from each other. The centre of mass of the rod is at distance x from A. The normal reaction on A is.. And on B is......
View SolutionA ladder AP of length 5m inclined to a vertical wall is slipping over a horizontal surface with velocity of 2m/s, when A is at distance 3m from ground. What is the velocity of COM at this moment?

View SolutionA particle A of mass 2m is held on a smooth horizontal table and is attached to one end of an inelastic string which runs over a smooth light pulley at the edge of the table. At the other end of the string there hangs another particle B of mass m, the distance from A to the pulley is l. The particle A is then projected towards the pulley with velocity u. (a) Find the time before the string becomes taut, and shown that after the string becomes taut, the initial velocity of A and B is 4u//3 . (b) Find the common velocity when A reaches the pulley (assume that B has not yet reached the ground).
View SolutionTwo particles A and B of equal mass m are attached by a string of length 2l and initially placed over a smooth horizontal table in the positoin shown in fig. particle B is projected across the table with speed u perpendicular to AB as shown in the figure. find the velocities of each particle after the string becomes taut and the magnitude of the impulse tension.
View SolutionA particle of mass 1kg is attached to a string of length 5m. The string is attached to a fixed point O. It is released from the position as shown in Fig. Calculate
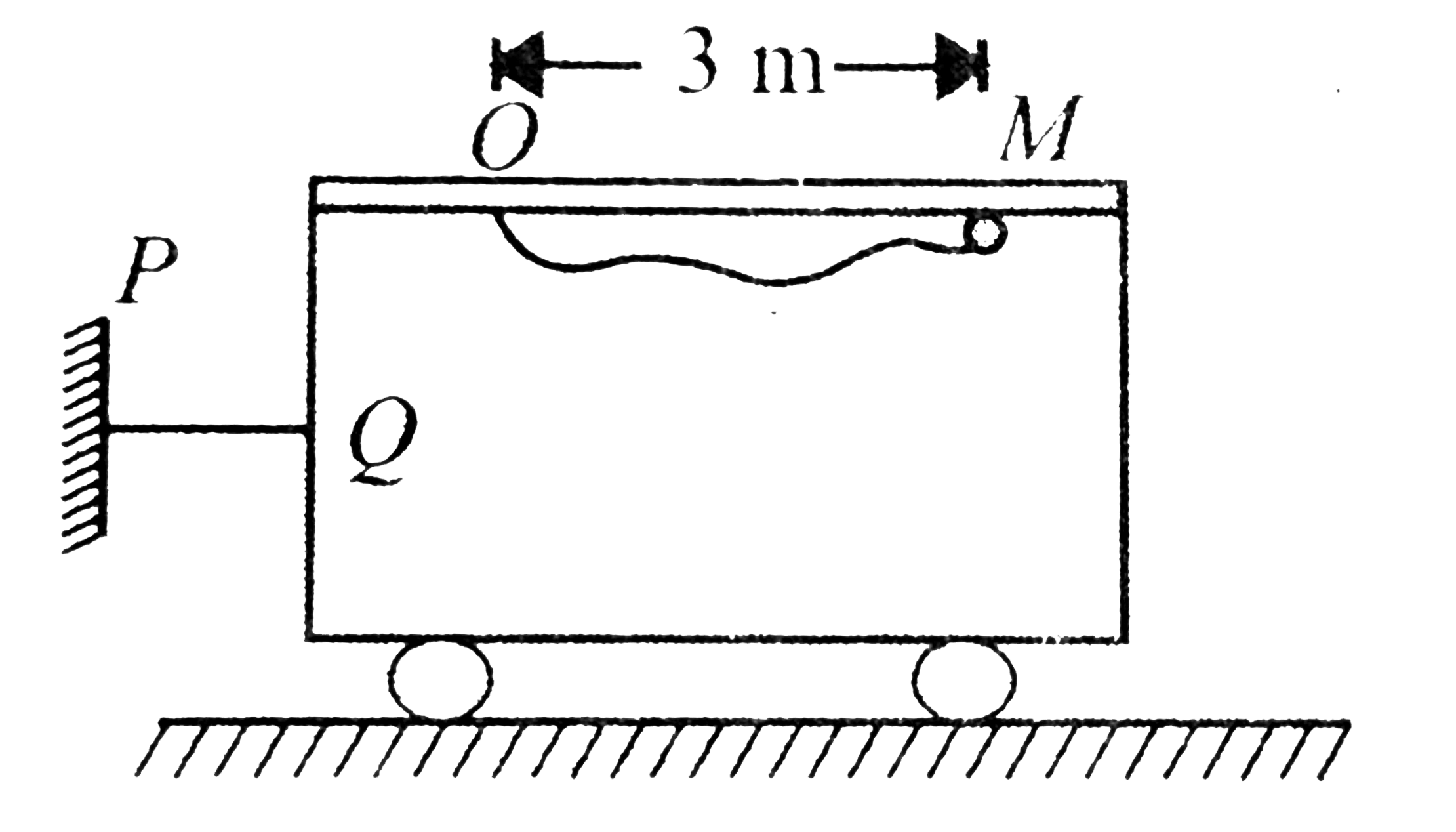
a. the impulse developed in the string when it becomes taut,
b. the velocity of the particle just after the string becomes taut,
c. the impulse developed in this string PQ at this instant.
View SolutionTwo particles, each of mass m, are connected by a light inextensible string of lenthe 2l . Initially they lie on a smooth horizontal table at points A and B distant l apart. The particle at A is projected across the table with velocity u. Find the speed with which the second particle begins to move if the direction of u is :- (i) along BA. (ii) at an angle of 120^(@) with AB (iii) perpendicular to AB. In each case calculate (in teerms of m and u) the impulsive tension in the string.
View SolutionTwo particles each of mass m are connected by a light inextensible string and a particle of mass M is attached to the midpoint of the string. The system is at rest on a smooth horizontal table with string just taut and in a straight line. The particle M is given a velocity v along the table perpendicular to the string. Prove that when the two particles are about to collide :
(i) The velocity of M is Mv(M+2m)
(ii) The speed of each of the other particles is (√2M(M+m)(M+2m))v.
View SolutionThere particles A, B and C have masses m, 2m and m respectively. They lie on a smooth horizontal table connected by light inextensible strings AB and BC. The string are taut and lt ABC = 120^(@) . An impulse is applied to particle A along BA so that it acquires a velocity u. Find the initial speeds of B and C.
View SolutionTwo particles, each of m, are connected by a light inextensible string of length 2l. Initially they lie on a smooth horizontal table at points A and B distant l apart. The particle at A is projected across the table with velocity u. Find the speed with which the second particle begins to move if the direction of u is , (a) along BA, (b) at an angle of 120∘ with AB, (c) perpendicular to AB. In each case calculate (in terms of m and u) the impulse of tension in the string.
View SolutionTwo particle, each of mass m, are connected by a light inextensible string of length 2l. Initially they lie on a smooth horizontal table at points A ad B distant l apart the particle at A is projectd across the table with velocity u. find th speed with which the second particle begins to move if the direction. of u is : (a). along BA (b). at an angle of 120^(@) with AB (c) perpendicular to AB In each case also calculate (in terms of ma nd u) the impulsive tension in the string.
View SolutionTwo particles of mass m and 2m are connected by a string of length L and placed at rest over a smooth horizontal surface. The particles are then given velocities as indicated in the figure shown. The tension developed in the string will be

View SolutionA string AB of length 21 is fixed at A to a point on a smooth horizontal table. A particle - of mass m attached to B is initially at a distance I from A as shown in figure. The particle is projected horizontally with speed u at right angles to AB. Find the impulsive tension in the string when it becomes taut and the velocity of the particle immediately afterwards.
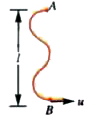
View SolutionTwo particles A and B of equal mass m each are attached by a string of length 21 and initally placed over a smooth horizontal table in the position shown in figure Particle B is projected across the table with speed u perpendicular to AB as shown in figure. Find the velocities of the particles after the string becomes taut and the magnitude of the impulsive tension.
View Solution
