A block of weight 5 units is placed on a horizontal table. A person pushes the block from top by exerting a downward force of 3 units on it. Find the force exerted by the table on the block.
To solve the problem of finding the force exerted by the table on the block, we can follow these steps:
Step 1: Identify the forces acting on the block
The block has two forces acting on it in the downward direction:
1. The weight of the block (W) = 5 units
2. The downward force exerted by the person (F) = 3 units
Step 2: Calculate the total downward force
To find the total downward force (F_total), we add the weight of the block and the downward force exerted by the person:
Ftotal=W+F=5units+3units=8units
Step 3: Understand the force exerted by the table
According to Newton's third law, the table will exert an upward force (normal force, N) equal to the total downward force acting on the block in order to keep it in equilibrium (since the block is at rest on the table).
Step 4: Set up the equilibrium condition
For the block to remain at rest, the upward force exerted by the table must equal the total downward force:
N=Ftotal
Step 5: Substitute the total downward force into the equation
Substituting the value we calculated:
N=8units
Conclusion
The force exerted by the table on the block is 8 units in the upward direction.
---
The block has two forces acting on it in the downward direction:
1. The weight of the block (W) = 5 units
2. The downward force exerted by the person (F) = 3 units
To find the total downward force (F_total), we add the weight of the block and the downward force exerted by the person:
Ftotal=W+F=5units+3units=8units
According to Newton's third law, the table will exert an upward force (normal force, N) equal to the total downward force acting on the block in order to keep it in equilibrium (since the block is at rest on the table).
For the block to remain at rest, the upward force exerted by the table must equal the total downward force:
N=Ftotal
Substituting the value we calculated:
N=8units
The force exerted by the table on the block is 8 units in the upward direction.
Topper's Solved these Questions
- FORCE AND LAWS OF MOTIONBOOK - MTG IIT JEE FOUNDATIONCHAPTER - FORCE AND LAWS OF MOTIONEXERCISE - SOLVED EXAMPLES
13 Videos
- FORCE AND LAWS OF MOTIONBOOK - MTG IIT JEE FOUNDATIONCHAPTER - FORCE AND LAWS OF MOTIONEXERCISE - NCERT SECTION
37 Videos
- FOOTSTEPS TOWARDS NEETBOOK - MTG IIT JEE FOUNDATIONCHAPTER - FOOTSTEPS TOWARDS NEETEXERCISE - Multiple Choice Question
45 Videos
- GRAVITATION BOOK - MTG IIT JEE FOUNDATIONCHAPTER - GRAVITATION EXERCISE - Olympiad/HOTS Corner
20 Videos
Similar Questions
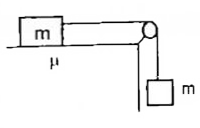
Two blocks, each of mass m are attached with a massless and inextensible string. One of the blocks is placed on the rough horizontal surface of a table for which coefficient of friction μ. Find out the force exerted by the table on the block if μ>1.
View SolutionA block of weight 20 N is placed on a horizontal table and a tension T is applied on the block . Tension can be increased to 8 N before the block begins to slide . A force of 4 N keeps the block moving at constant speed , once it has been set in motion . Find the coefficients of static friction and kinetic friction].
View Solution
Knowledge Check
A block is placed on a horizontal table. Identify the force of action
Aweight of blockBsupport of table on the blockCeither (a) or (b)Dneither (a) nor (b).When a block is kept on the table, its weight acts vertically downwards then the force exerted by the surface on the block is
Avertically upwards called normal reaction.Bvertically downwared called normal reaction.Ctangential force acting along the motion .Dtangential force acting opposite to the motion.A block of mass 70kg is kept on a rough horizontal surface (μ=0.4) . A person is trying to pull the block by applying a horizontal force, but the block is not moving. The net contact force exerted by the surface on the block is F , then:
AF=280NBF=754NCF=700ND700N≤F≤754N
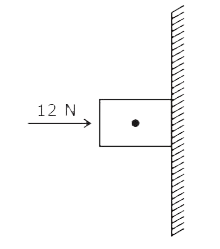
A block of weight 5N is pushed against a vertical wall by a force 12 N. The coefficient of friction between the wall and block is 0.6. The magnitude of the force exerted by the wall on the block is
View SolutionA cubical block of wood of length 5 cm is kept on a table top. The density of the block is 800kg/m3 and g=9.8m/s2 . Find the pressure exerted by the wooden block on the table top.
View SolutionA block of mass 1 kg is placed on a horizontal surface . The reaction force to the weight of the block is
View SolutionA block of mass m2 is placed on a horizontal table and another block of mass m1 is placed on top of it. An increasing horizontal force F = at is exerted on the upper block but the lower block never moves as a result. If the coefficient of friction between the blocks is μ1 and that between the lower block and the table is μ2, then what is the maximum possible value of μ1/μ2?
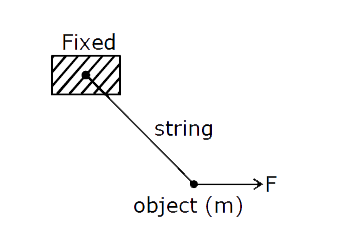
View SolutionIn the following figure, the object of mass m is held at rest by a horizontal force as shown. The force exerted by the string on the block is -
View Solution
