A block suspended from a vertical spring is in equilibrium. Show that the extension of the spring equals the length of an equivalent simple pendulum, i.e., a pendulum having frequency same as that of the block.
The correct Answer is:A
To solve the problem of showing that the extension of a spring (x₀) equals the length of an equivalent simple pendulum (L) with the same frequency, we can follow these steps:
1. Understanding the Forces:
- A block of mass m is suspended from a vertical spring. At equilibrium, the weight of the block (mg) is balanced by the restoring force of the spring (kx₀), where k is the spring constant and x₀ is the extension of the spring.
- Therefore, at equilibrium, we have:
kx₀=mg
2. Finding the Extension:
- Rearranging the equation from Step 1 gives us the extension of the spring:
x₀=mgk
3. Frequency of the Spring-Mass System:
- The frequency f of the spring-mass system is given by:
f=12π√km
4. Frequency of the Simple Pendulum:
- The frequency of a simple pendulum is given by:
f=12π√gL
- Where g is the acceleration due to gravity and L is the length of the pendulum.
5. Equating Frequencies:
- Since the frequencies of both systems are equal, we can set their expressions equal to each other:
12π√km=12π√gL
6. Simplifying the Equation:
- Canceling 12π from both sides, we get:
√km=√gL
7. Squaring Both Sides:
- Squaring both sides gives:
km=gL
8. Rearranging to Find L:
- Rearranging the equation to solve for L, we have:
L=mgk
9. Substituting for x₀:
- From Step 2, we know that x₀=mgk. Therefore, we can substitute this into our equation for L:
L=x₀
Conclusion:
We have shown that the extension of the spring x₀ equals the length of an equivalent simple pendulum L.
- A block of mass m is suspended from a vertical spring. At equilibrium, the weight of the block (mg) is balanced by the restoring force of the spring (kx₀), where k is the spring constant and x₀ is the extension of the spring.
- Therefore, at equilibrium, we have:
kx₀=mg
- Rearranging the equation from Step 1 gives us the extension of the spring:
x₀=mgk
- The frequency f of the spring-mass system is given by:
f=12π√km
- The frequency of a simple pendulum is given by:
f=12π√gL
- Where g is the acceleration due to gravity and L is the length of the pendulum.
- Since the frequencies of both systems are equal, we can set their expressions equal to each other:
12π√km=12π√gL
- Canceling 12π from both sides, we get:
√km=√gL
- Squaring both sides gives:
km=gL
- Rearranging the equation to solve for L, we have:
L=mgk
- From Step 2, we know that x₀=mgk. Therefore, we can substitute this into our equation for L:
L=x₀
We have shown that the extension of the spring x₀ equals the length of an equivalent simple pendulum L.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer
15 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective-2
15 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer
21 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Objective-2
7 Videos
Similar Questions
Knowledge Check
A spring has force constant K and a mass m is suspended from it. The spring is cut in half and the same is suspended from one of the havles. IF the frequency of osicllation in the frst case is α, then the frequency in the second case will be
A2 aBaCa/2Dα/√2
Two springs are in a series combination and are attached to a block of mass 'm' which is in equilibrium. The spring constants and extension in the springs are as shown in the figure. Then the force exerted by the spring on the block is :

View Solution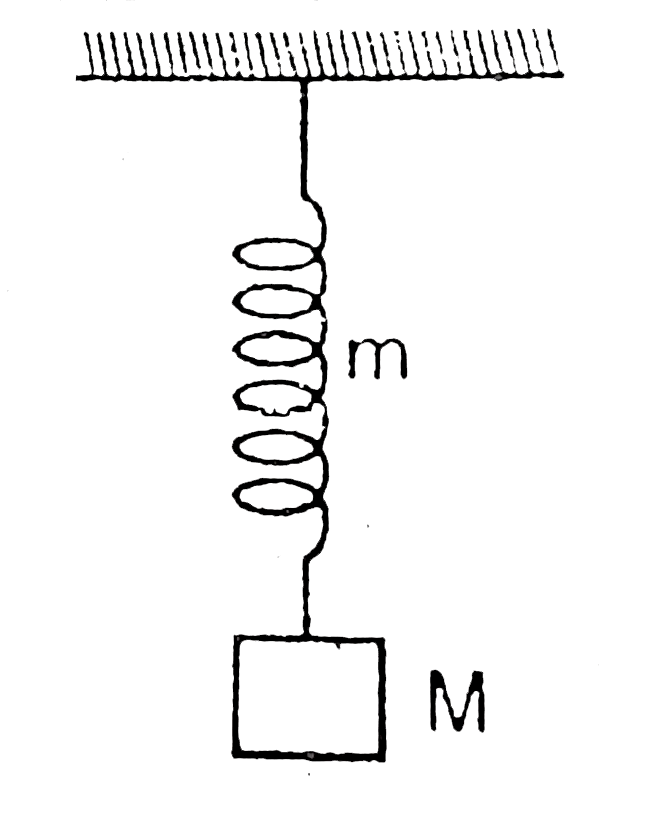
A block of M is suspended from a vertical spring of mass m as shown in the figure. When block is pulled down and released the mass oscillates with maximum velocity v.
View SolutionA block of mass m is suspended through a spring of spring constant k and is in equilibrium. A sharp blow gives the block an initial downward velocity v. How far below the equilibrium position, the block comes to an instantaneous rest?
View SolutionA mass m is suspended from a spring. Its frequency of oscillation is f. The spring is cut into two halves and the same mass is suspended from one of the pieces of the spring. The frequency of oscillation of the mass will be
View SolutionIn the diagram below, A, B, C, D are four pendulums suspended from the same elastic string PQ. The length of A and Care equal to each other while the length of pendulum B is smaller than that of D. Pendulum A is set into a mode of vibrations.

What is the state of pendulum C?
View SolutionA block of mass M suspended from a spring oscillates with time period T. If spring is cut in to two equal parts and same mass M is suspended from one part, new period os oscillation is
View SolutionA block of mass M suspended from a spring oscillates with time period T. If spring is cut in to two equal parts and same mass M is suspended from one part, new period os oscillation is
View Solution

